Hosmer-Lemeshow检验(HL检验)为模型拟合指标,其原理在于判断预测值与真实值之间的gap情况,如果p值大于0.05,则说明通过HL检验,即说明预测值与真实值之间并无非常明显的差异。反之如果p值小于0.05,则说明没有通过HL检验,预测值与真实值之间有着明显的差异,即说明模型拟合度较差。
二元logit回归分析步骤一般如下:

数据预处理 因为二元logistic回归的因变量为二分类变量并且只能为0和1,所以如果数据不是0和1,需要在分析前进行处理,可以利用SPSSAU进行数据编码,即可满足分析要求。

单因素显著性检验(可不做)
当因变量满足要求后,接下来我们可以对因变量和自变量进行简单初步判断,研究自变量对因变量是否存在显著性差异,由于数据类型可能存在不同,所以检验的方法也会不同,最常用的三种方法分别是卡方检验(定类和定类)、t检验(定类和定量,定类数据为两组),可以通过判断分析结果的p值判断自变量对因变量是否存在显著性差异。由于例子中自变量没有定类变量所以进行t检验进行演示:

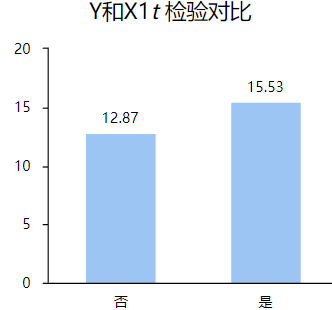
从上表可以看出,X1、X2、X3、X4四项p值均小于0.05,所以这四项对Y均有显著性差异,并且观察平均值和标准差,每项选择否和是的均值差距也较大,利用可视化图形能够更直观的观察到,比如Y和X1,Y和X2如下:

构建二元Logistic回归模型
由单个因素进行分析发现X1-X4对于因变量Y都有显著性差异,所以在分析时可以将自变量都放进模型中,对于二元logistic回归分析SPSSAU共提供三种方式分别是逐步法,向前法和向后法。
逐步法
通过在基于 F 检验的现有模型中添加或删除预测变量,执行变量选择。逐步法是向前选择法与向后消元法程序的组合。如果初始模型使用所有的自由度,则逐步选择操作不会继续。
向前法
确定要在模型中保留哪些项的方法。向前选择法会使用与逐步过程相同的方法向模型添加变量。
向后法
确定要在模型中保留哪些变量的方法。向后消元法以包含所有项的模型开始,然后使用与逐步过程相同的方法一次一个删除这些项。不能将变量重新输入模型。当模型中的变量不包含大于删除用 Alpha中指定值的 p 值时,默认向后消元过程将结束。
本例子选取逐步法进行分析并展示结果。

自变量为X1、X2、X3、X4因变量为Y,二元logit回归分析方法选择逐步法,最后模型留下的自变量为X2、X3和X4。可以发现此三项对因变量的解释程度约为0.6。由表格中的回归系数可以看出,X2的回归系数为0.038,X3的回归系数为0.076,X4的回归系数为0.012,截距的回归系数为-9.897,所以模型公式为:ln(p/1-p)=-9.897 + 0.038*X2 + 0.076*X3 + 0.012*X4(其中p代表Y为1 的概率,1-p代表Y为0的概率)。接下来对模型进行评估。
模型评估
从三个方面进行说明,其中模型有效性检验、拟合优度以及预测准确性。
模型有效性

对于-2倍对数似然值常用来反映模型的拟合程度,其值越小,表示拟合程度越好,一般用于不同模型之间比较等。从结果可以看出p值远小于0.05,从而可以说明本次模型构建有效。接下来查看拟合优度。
拟合优度

对于H-L检验,一般p值大于0.05,说明模型拟合良好,p<0.05说明模型拟合欠佳,从结果可得p值大于0.05,说明模型拟合良好。
预测准确性

通用预测准确率汇总,最终可以发预测准确率为91.35%,预测错误率为8.65%,所以预测较为准确(如果研究者分析目的不在于预测模型,则此步可省略)。



























 1388
1388

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








