在科研与决策领域,评价指标体系的构建及其权重计算是至关重要的步骤。本文将详细介绍这一过程,探讨如何科学地构建一套完整、合理的评价指标体系,并介绍计算各指标权重的常用方法,包括主观赋权法、客观赋权法以及组合赋权。
一、评价指标体系构建
本文以知网中一篇关于G公司财务绩效评价的论文为例,展示如何构建评价指标体系及运用AHP-熵值法进行组合赋权。论文首先确定了评价指标,接着采用AHP法结合专家意见确定主观权重,并通过熵值法对指标数据进行客观分析,最终将两种权重结合,得出综合权重。部分目录展示如下:

夏云云. 基于AHP-熵值法的G公司财务绩效评价研究[D]. 东华理工大学, 2020.
构建评价指标体系的组合赋权法通常涉及四个主要环节:首先是建立评价指标体系,其次是利用层次分析法(AHP)来确定权重,然后通过熵值法来计算权重,最后是综合各权重以确定组合权重(注意,权重的计算方法不唯一,可根据情况选择)。
1、评价指标体系构建
首先需要基于一定的思想和原则进行评价指标体系的构建,先搭建一个框架,通常包括目标层、准则层(一级指标)、方案层(二级指标),如下图:
- 目标层(评价目的):这是评价指标体系的最高层次,它明确了评价的目的和意义。目标层通常是一个宏观的、抽象的描述,指出了评价活动的总体方向。
- 准则层(评价准则):准则层是目标层的具体化,它将评价目标分解为若干个可以操作的评价准则或评价维度。这些准则应当能够全面反映目标层的各个方面。
- 方案层(评价指标):方案层是评价指标体系中的最底层,它由一系列具体的、可量化的指标组成。这些指标是评价的直接依据,它们应当具有独立性、可测性、代表性和可比性。
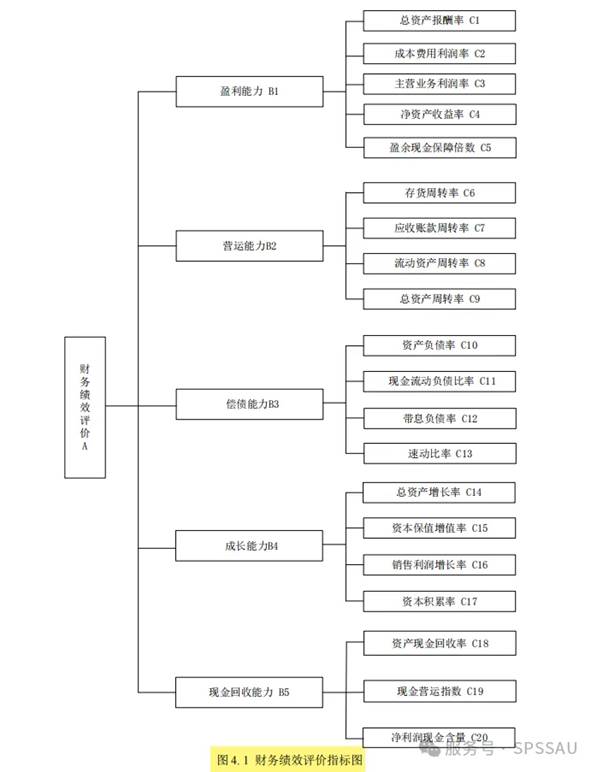
第一步,确立指标并构建评价体系,同时搜集所需数据。这一环节需由研究者根据论文的研究目的自主完成,建议研究者广泛查阅并深入研读多篇相关领域的学术论文。
在此过程中,可以注重对比不同论文中指标的选取原则、评价体系的构建方法以及数据收集的途径和技巧,从而为自己的研究提供有益的参考和借鉴。同时,也可结合自身的研究实际,灵活调整和优化指标选取和评价体系构建的策略。
2、AHP层次分析法权重计算
评价指标体系构建完成后,使用层次分析法计算指标主观权重。层次分析法计算指标权重时,一般先计算准则层权重,再依次计算方案层权重,然后将准则层权重和方案层权重相乘得到最终权重。
- 首先准则层盈利能力B1、营运能力B2、偿债能力B3、成长能力B4、现金回收能力B5 构造判断矩阵计算权重值;
- 然后B1的下属方案层指标C1~C5构造判断矩阵计算权重值,B2的下属方案层指标C6~C9构造判断矩阵计算权重值,其余类似依次进行层次分析法。
- 最后将准则层权重和方案层权重相乘得到综合权重,整理成下表:

AHP层次分析法SPSSAU软件操作:选择判断矩阵阶数,填写白色单元格,点击开始分析按钮,如下图:
SPSSAU输出层次分析法权重计算及一致性检验结果如下:

主观权重计算完成后接下来计算客观权重。
3、熵值法权重计算
采用熵值法(或其他相应方法)来确定指标的客观权重。在组合赋权过程中,通常多数文献直接运用熵值法计算方案层指标的权重,所得权重结果如表所示。
熵值法SPSSAU软件操作:上传数据至SPSSAU平台,将量纲处理后的数据进行熵值法分析,如下图:

SPSSAU输出熵值法权重计算结果如下:
此时主观权重和客观权重都已经得到,接下来就是将两次权重结果进行组合,计算最终的组合权重也称综合权重。
4、组合权重计算方法
组合权重计算方法有很多种,没有一个固定的选择标准。如加法合成法、乘法合成法、极差最大化、矩阵思想、线性组合赋权等等。比如本案例中使用的方法为简单的加法合成法,计算公式如下:
 最终计算得到AHP-熵值法的组合权重,将结果整理成下表:
最终计算得到AHP-熵值法的组合权重,将结果整理成下表:
那么此时一个完整的评价指标体系就构建完成了,最后就可以根据你的研究目的进行综合评价分析或者其他分析。
二、11种权重计算方法
论文中最高频使用的权重计算方法就是上文介绍的层次分析法与熵值法,除此之外,还有很多权重计算方法,可分为主观赋权法与客观赋权法两类,常用的11种权重计算方法如下:

下表简单对比了以上11种权重计算方法的适用场景,以及优缺点。

接下来分别介绍这11种权重计算方法。
三、主观赋权法
主观赋权法是基于决策者或专家的主观判断来确定指标权重的方法。它通常依赖于专家的经验、知识、直觉和偏好,通过直接评分、排序、德尔菲法等方式来分配权重。
- 主观赋权法的优点:是能够充分考虑决策者的意愿和偏好,适用于指标难以量化或信息不充分的情况;
- 主观赋权法的缺点:是结果受主观因素影响较大,可能缺乏客观性和稳定性。
1、AHP层次分析法
AHP层次分析法是一种定性与定量相结合的多准则决策方法。它将复杂的决策问题分解为多个层次,通过两两比较各层次元素的重要性,构建判断矩阵,并计算各元素的相对权重,最终为决策提供依据。
2、模糊层次分析法
模糊层次分析法(FAHP)是在传统AHP基础上,结合模糊集理论发展而来的一种决策方法。它允许在比较元素重要性时使用模糊语言变量,从而处理决策中的不确定性和模糊性。FAHP适用于那些难以精确量化或存在模糊性的决策问题,如风险评估等。
3、优序图法
优序图法是一种通过比较评价指标来确定重要性排序的方法。它利用专家打分或问卷调查等方式,对各项指标进行两两比较,根据比较结果构建优序图,并通过计算得出各项指标的权重。优序图法操作简单,直观易懂,适用于指标数量较少且需要快速确定权重的场景。
4、德尔菲法
德尔菲法是一种通过匿名函询专家意见来收集信息并进行预测或决策的方法。在权重计算中,德尔菲法可以通过多轮函询专家对各指标重要性的看法,逐步收敛专家意见,最终确定各指标的权重。这种方法能够充分利用专家的知识和经验,但在时间和成本上可能较高。
5、最好最差权重BWM
最好最差权重法是一种简化的多准则决策方法。它只要求决策者识别出所有准则中的“最好”和“最差”准则,并比较它们与其他准则的相对重要性,从而计算出各准则的权重。BWM方法简单直观,减少了比较次数,提高了计算效率,适用于需要快速决策且准则数量较多的场景。
四、客观赋权法
客观赋权法是基于数据本身的统计特性或数学规律来确定指标权重的方法。它不依赖于人的主观判断,而是通过计算指标之间的相关系数、变异程度、信息量等客观指标来分配权重。
1、熵值法
熵值法利用数据熵值信息即信息量大小进行权重计算。此类方法适用于数据之间有波动,同时会将数据波动作为一种信息的方法。熵值法在论文中使用频率很高。
2、主成分分析&因子分析
主成分分析法和因子分析法确定权重时利用了数据降维处理原理,主要利用特征根、方差解释率、载荷系数进行权重计算。
3、CRITIC权重、独立性权重、信息量权重
这三种权重确定方法,主要利用数据的波动性或数据之间的相关关系情况进行权重计算。其中,独立性权重法使用复相关系数计算权重;信息量权重法使用数据变异系数计算权重;而 CRITIC 权重法则是综合数据的波动性和指标间的相关性计算权重。
独立性权重法、信息量权重法的使用范围相对较小,使用时应谨慎,CRITIC权重法使用范围较广,得到了广泛使用。























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








