一文理清4类t检验分析步骤，软件操作与分析结果解读

一、t检验分析步骤

在统计学上，t检验的步骤是研究者首先提出原假设(H0,两均值相等)和备择假设(H1,两均值不相等)，然后用数据构造并计算t统计量，接着通过t分布计算概率p值，最后利用p值推断原假设是否成立，从而完成整个假设检验流程。实际科研数据分析中，综合t检验类型、适用条件，总结出t检验分析方法应用的分析思路，见图 4‑2。

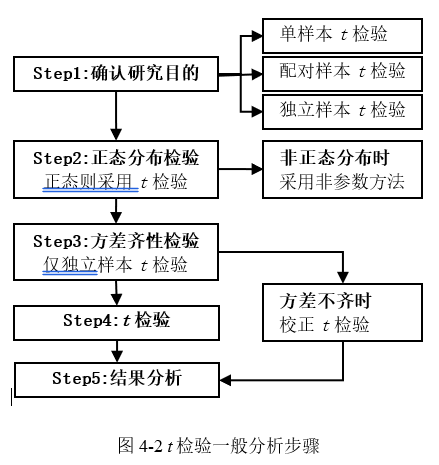
1) 根据科研设计与研究目的，选择单样本t检验、配对样本t检验、独立样本t检验中的一种，比如配对设计选择配对样本t检验，成组设计选择独立样本t检验。

2) 对两组数据进行正态分布检验，满足条件时使用t检验，非正态分布(或严重偏离正态分布)时考虑数据转换再做t检验或采用非参数秩和检验方法(单样本和配对t检验对应的是Wilcoxon检验、独立样本t检验对应的是Mann-Whitney检验)。

3) 如果研究目的是比较成组设计两组均数的差异，即选择独立样本t检验时，还应对两组数据是否方差齐次进行检验。

4) 由统计软件工具执行t检验，如遇到方差不齐则对t检验进行校正。

5) 对结果进行分析，撰写结论。按α=0.05水平，当t检验概率p值小于0.05时，认为两组均数差异有统计学意义，反之p大于0.05说明无差别。

分析一组数据的均数是否与给定常数之间存在差异，是用随机抽取的单个样本均数和已知总体均数进行比较，观察该组样本与总体的差异性，例如研究人员考察某地新生儿的平均体重与同类大型研究常模体重的差异。要求该组样本数据服从正态分布，且没有明显异常数据。

二、单样本t检验案例分析

【例4-2】已知某地区12岁男孩平均身高为142.5cm(常模数据)。1973年某市测量120名12岁男孩身高资料，试分析该市12岁男孩与该地区12岁男孩身高平均值是否相等。案例数据来源于卢纹岱(2006)，数据文档见“例4-2.xls”。

1) 数据与案例分析

数据文档中的“身高”为定量数据，用于记录120名男孩的身高数据，研究目的是比较120个身高数据平均值与“142.5”的差异，从分析目的上选择单样本t检验。

2) 正态分布检验

经【通用方法】→【正态性检验】模块，选择Shapiro-Wilk检验，p=0.93﹥0.05，说明该组数据服从正态分布，满足单样本t检验对数据正态性的要求。

3) 单样本t 检验

数据文档读入平台后，在仪表盘中依次选择【通用方法】→【单样本t检验】模块，将“身高”变量数据拖拽至右侧【分析项(定量)】框内，分析框顶部输入对比数字“142.5”，操作界面见下图，单击【开始分析】。

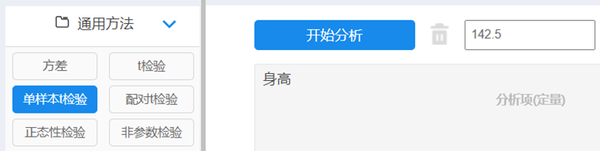
4) 结果分析

t检验结果如表 4‑4所示，第2～6列为常见描述统计指标，第7～8列为t统计量和概率p值。

120名12岁男孩身高平均值为143.048cm，与该地区12岁男孩身高的一般水平142.5cm相比，t=1.032, p=0.304﹥0.05，差异无统计学意义。

三、配对样本t检验案例分析

配对设计常见的形式是自身配对或非自身配对。例如对同一研究对象在试验干预前、干预后的某指标数据进行比较；同一研究对象在两个不同部位所测定某指标数据进行比较；又或者同源配对或条件相近者异体配对数据结果的比较。

配对设计所获两组数据，因其本身具有相关性，所以需要使用针对性的分析方法。配对样本t检验，可用来检验有配对或相关关系的两组数据均数是否相等。统计分析时取2组配对数据的差值与数字“0”进行差异比较。使用条件上，要求配对的两组样本数据差值服从正态分布。

【例4-3】10名高血压患者在实施体育疗法前后测定舒张压，请判断体育疗法对降低血压是否有效。案例数据来源于卢纹岱(2006)，数据文档见“例4-3.xls”。

1) 数据与案例分析

体育疗法前、后的舒张压数据分别为“治疗前”、“治疗后”两个定量数据，本例属于自身前后配对设计，综合考虑采用配对样本t检验进行差异比较。

2) 正态分布检验

通过【数据处理】→【生成变量】的“相减(Minus)”功能，计算得到“差值”数据，经【通用方法】→【正态性检验】模块的Shapiro-Wilk检验，p=0.225﹥0.05，说明差值数据服从正态分布，满足t检验对正态性的要求。

3) 配对t 检验

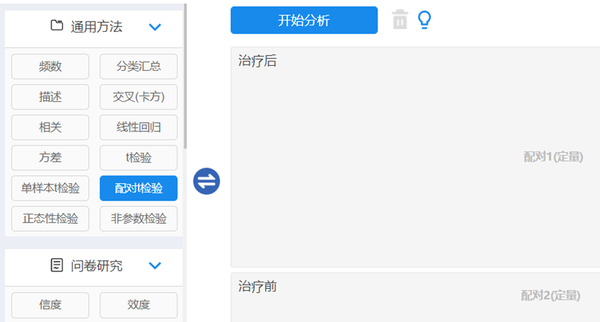
数据文档读入平台后，在仪表盘中依次选择【通用方法】→【配对t检验】模块，将“治疗后”变量数据拖拽至右侧【配对1(定量)】框内，“治疗前”变量数据拖拽至右侧【配对2(定量)】框内。相关操作设定如图 4‑4所示，最后单击【开始分析】。

4) 结果分析

配对t检验结果见表 4‑5。表格中第2～3列为配对前后舒张压描述统计，第4列为配对前后的差值，最后两列为t统计量和p值。

体育疗法前高血压患者的舒张压为(119.50±10.07)，治疗后的舒张压为(102.50±11.12)，显然治疗后舒张压出现了下降。

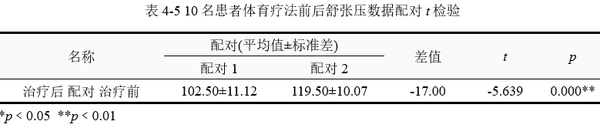
差值为-17，说明治疗后舒张压下降17个单位，如果差值与数字“0”相比差异显著，即可说明配对的两个样本均值差异有统计学意义。t=-5.639，p﹤0.01，按α=0.01水平，认为体育疗法治疗后高血压患者的舒张压下降明显，与治疗前相比差异有统计学意义，该疗法对降低高血压患者舒张压有效。

四、独立样本t检验

采用成组设计，检验两组数据各自总体均数是否相等。例如研究人员想比较不同性别人群的抑郁评分是否有显著差异。t 检验仅可对比两组独立成组数据的差异，如果为三组或多组，则使用方差分析。

独立样本t检验要求两组数据分别服从正态分布，且两组数据的方差齐性。所谓方差齐性，即要求两组数据的总体方差相同。

【例4-4】沿用“例4-1”的数据，某研究收集到100例儿童的腰围(cm)数据，其中肥胖组50例，另外50例为非肥胖组。数据文档见“例4-4.xls”，试分析肥胖组与非肥胖组儿童的腰围有无不同。

1) 数据与案例分析

“组别”变量编码1表示肥胖组，编码0表示非肥胖组，“腰围”记录两组儿童的腰围数据，为定量数据。本例为成组设计，目的是比较两组儿童腰围的差异，应采用独立样本t检验。

2) 正态分布与方差齐性条件判断

经【通用方法】→【正态性检验】模块Shapiro-Wilk检验，两组数据的显著性p值分别为0.11、0.971均大于0.05，说明数据服从正态分布。方差齐性已在“例4-1”中讨论，F=2.576，p=0.112﹥0.05，表明两组数据的方差齐。

3) 独立样本t 检验

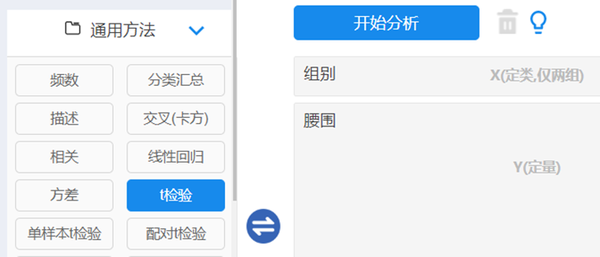
数据文档读入平台后，在仪表盘中依次选择【通用方法】→【t检验】模块。将“组别”数据拖拽至右侧【Y(定量)】框内，“腰围”数据拖拽至右侧【X(定类,仅两组)】框内，操作界面如图 4‑5所示，最后单击【开始分析】。

4) 结果分析

独立样本t检验分析结果，见表 4‑6。

肥胖组儿童的腰围为(61.02±5.41)cm，非肥胖组腰围为(52.52±3.95)cm。t=-8.965，p﹤0.01，按α=0.01显著性水平，有理由认为肥胖组与非肥胖组儿童的腰围差异显著。

五、概要t检验

对于两样本均数的比较，或单样本与总体均数的比较，如果只有汇总后数据比如平均值、标准差，这一类t检验问题需要使用统计摘要信息进行检验，一般称为概要t检验。

概要t检验包括两种，分别是单样本t检验和独立样本t检验。前者是一组数据与某数字的差异比较，后者是两组数据的平均值差异比较。要求其原始数据服从正态性条件。

具体分析时，需要提供单样本或两样本的平均值、标准差，以及样本量指标值，并不需要额外进行正态性和方差齐性的检验。

【例4-5】单样本概要t检验。某年某地区测量120名12岁男孩身高资料，平均身高143cm，标准差为5.8cm。历史资料显示该地区12岁男孩平均身高为142.5cm，试分析该样本平均身高与历史一般水平有无差异。

1) 案例分析

本例为汇总后的摘要数据资料，研究者仅知道平均值、标准差、样本量等统计摘要信息，研究目的是单样本均数与已知均数进行比较。应使用单样本的概要t检验进行分析。

2) 概要t检验

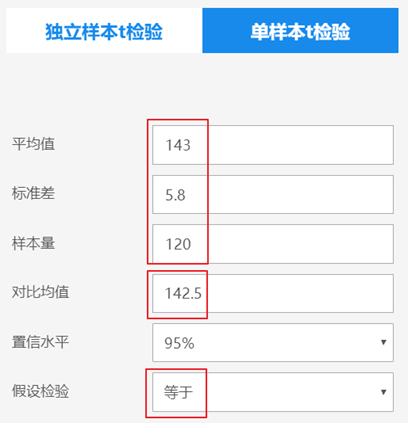
无原始数据，仪表盘中依次打开【实验/医学研究】→【概要t检验】→【单样本t检验】模块。依次输入平均值“143”、标准差“5.8”、样本量“120”、对比均值“142.5”。默认是进行双侧假设检验，如遇单侧问题，则根据具体情况修改【假设检验】为大于或小于。具体设置如图 4‑6所示。

3) 结果分析

如表 4‑7所示，120名男孩平均身高为143cm，总体平均身高的95% CI为[141.95,144.05]cm。

与该地区12岁男孩历史资料的平均身高142.5cm相比，t=0.94，p=0.35﹥0.05，按α=0.05水平，差异无统计学意义，尚不能认为该样本平均身高与历史一般水平存在差异。具体结果见表 4‑8。

以上内容摘自《SPSSAU科研数据分析方法与应用》第4章——差异关系研究，书中不仅涵盖了数据清理、统计分析和模型构建等内容，还提供了丰富的案例，以便于读者在实际研究中应用。