方差分析入门知识 | 分析方法概述与方差分析类型

t检验针对的是两组数据均值的差异比较，如果是三组及多组数据均值的比较，则需采用方差分析。方差分析的基本思想是对数据的总变异进行分解，将各部分的方差与误差相比较，从而判断因素或交互作用的统计学意义。

本节主要介绍只有一个因变量Y的方差分析。只有一个自变量X的方差分析称为单因素方差分析，有两个自变量X则称之为双因素方差分析，当自变量因素个数超过两个时，统称为多因素方差分析。

一、方法概述

1. 原理与概念

方差分析的基本思想是对误差的分解，总误差被分解为组间误差和组内误差，组内误差用于估计抽样的随机误差，而组间误差可能是由抽样的随机误差造成，更多的是组间自身差异的系统误差导致。我们需要证明的是系统误差不等于0，所以组间误差除以组内误差大到一定程度时可认为组间效应显著。为消除个案数的影响，给分母和分子同时引进自由度，构造F统计量，根据F分布计算概率p值，利用p值推断原假设是否成立。所以，方差分析等价于F检验，中间计算的统计量为F统计量。

方差分析中的常用概念术语包括：

(1) 因素：方差分析是从组间差异比较来推断自变量对因变量的影响，此处的自变量通常也称作因素或因子。例如超市某商品销售量的影响因素有商品价格、货架摆放位置、广告宣传等。

(2) 水平：方差分析中的因素要求是定类数据，因素的不同类别取值称作水平。例如商品在货架的摆放位置有低、中、高三个水平，商品价格有原价、促销活动价格两个水平。

(3) 组合或单元：各因素不同水平的交叉称为组合或单元，例如某商品摆放在货架中间层且以促销价格销售时更有利于售卖。

(4) 主效应：指某一因素各单独效应的平均效应，即某一因素各水平之间的平均差别。一个因素的主效应显著，意味着该因素的各个水平在其它因素的所有水平上的平均数存在差异。

(5) 交互作用：是反映两个或两个以上因素相互依赖制约、共同影响因变量的变化。如果一个因素对因变量的影响会因另一个因素的水平不同而有所不同，则可以说这两个变量之间具有交互作用。

2. 方差分析的适用条件

方差分析要求因变量Y为定量数据(连续型数据)，自变量X为定类数据(分类数据)。如果需控制混杂干扰，则需加入协变量，协变量也要求为定量数据。

进行方差分析需要数据满足以下两个基本前提：

(1) 各观测变量数据总体要服从正态分布；

(2) 各观测变量数据的总体满足方差齐性；

理论上，数据须满足以上两个条件才能进行方差分析。实际分析时，可根据试验设计方法、数据样本量、行业一般要求，以及检验方法的结果综合讨论并对两个条件作出判断，通常因方差分析本身较为稳健，因此可适当放宽两个条件，具体结合文献资料而定。

对于非正态分布数据，可以考虑做正态转换使数据满足正态要求后继续方差分析，或当严重偏离正态分布时采用非参数秩和检验作为替代；对于方差不齐的情况，可使用非参数秩和检验，同时也可以选择使用更为稳健的Welch 方差分析或者Brown-Forsythe方差分析，其中Welch 方差分析较为常用。

正态分布条件的判断，可参考《SPSSAU科研数据分析方法与应用》第2章节的内容。非参数秩和检验可在本章节4.4节查阅相关内容。

3. 事后多重比较

单因素方差分析的F检验p值小于0.05即总体上组间差异显著时，则需要继续对因素各水平间的差异进行两两配对的多重比较，双因素或多因素方差分析在交互作用不显著的前提下，也需要继续针对各有显著影响的因素主效应进行多重比较。

例如：对四所中学(全国重点、市重点、区重点、一般中学)某年级数学统一测试成绩进行方差分析，结果显示不同中学间成绩有显著差异。这是总体结论，究竟哪些中学之间有差异？比如全国重点中学与市重点中学间成绩有无差别，市重点和一般中学间成绩有无差别，这就需要进一步分析。这一过程所采用的方法就称之为多重比较，通过对总体均值之间的两两配对比较进一步分析到底哪些均值间存在差异。

事后多重比较的方法有多种，SPSSAU【事后多重比较】模块中共提供LSD、Scheffe、Tukey、Bonferroni校正、Sidak、Tamhane T2、SNK、Duncan检验等8种常用方法，如表 4‑10所示。

4.差异比较结果的字母标记

差异的字母标记法是指使用不同字母方式标记注释出多重比较的差异结果，如果对比的组之间有相同字母即表示差异不显著，如果字母不同则表示两组间差异显著。

SPSSAU默认提供0.01和0.05两种不同显著性水平时的字母标记法结果，0.05水平时使用小写字母标识，0.01水平时使用大写字母标识，具体结果由【进阶方法】→【事后多重比较】模块完成。

二、方差分析类型的选择

数据分析时采用何种类型的方差分析，可参考试验设计方法与研究分析目的综合决定。

1. 试验设计方法与方差分析类型

通常情况下，方差分析与科学试验设计相辅相成。在考虑使用方差分析方法时，应结合研究分析目的及科学试验所用的设计方法进行综合考虑。常见试验设计与方差分析方法类型的选择思路，见表 4‑11。

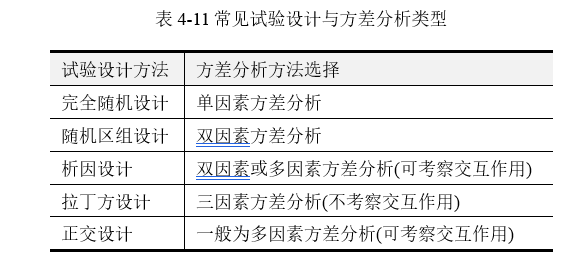
(1) 完全随机设计有时也称为单因素设计，是将被试随机化分配到各处理组中，仅考察一个处理因素对试验指标的影响。统计方法采用单因素方差分析，如果该因素有统计学意义，则继续进行各组均数间的多重比较。

(2)随机区组设计是将被试划分为区组，再将每一区组的被试随机分配到各个处理组中，每个区组的样本量等于处理组的个数。随机区组设计可采用双因素方差分析进行结果分析，一般认为区组因素是次要因素，通常不需要考察区组与处理因素间的交互作用。

(3) 析因设计也叫做全因子设计，是试验中所涉及到的全部因素的各水平全面组合形成不同的试验组合，每个试验组合下进行两次或两次以上的独立重复实验。它不仅可检验每个因素各水平间的差异，而且可检验各因素间的交互作用。统计方法采用双因素方差分析或多因素方差分析，可考察因素间的交互作用。

(4) 拉丁方设计是随机区组设计的扩展，如果研究涉及一个处理因素和两个需要控制的区组因素，每个因素的水平数相等，此时可采用拉丁方设计。统计分析方法采用多因素方差分析，但须注意拉丁方设计不能考察交互作用。

(5) 试验因素较多且希望考察交互作用，用最少的试验次数获得较佳的试验结果，此处可采用正交设计。统计方法采用多因素方差分析，且根据正交试验方案的不同可考察因素间的交互作用。

2. 研究分析目的与方差分析类型

科研数据分析中的差异关系研究是错综复杂的，单个因素的分析往往是作为基础性工作，更多情况下需要综合考虑多个因素的关系或联系。方差分析可以是一个因素，也可以是多个因素，还可以分析因素间的交互作用，因此应用范围较为广泛。

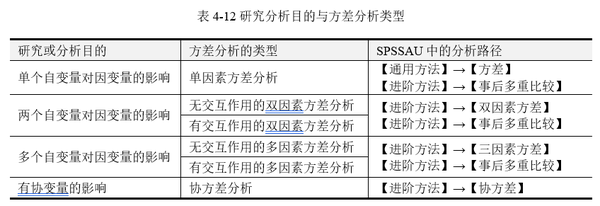
根据研究分析目的的不同，可使用单因素、双因素、多因素方差分析以及协方差分析。有两个及以上因素时，又可分为有交互作用的方差分析和无交互作用的方差分析。研究分析目的与方差分析类型，见表 4‑12。SPSSAU平台在【通用方法】、【进阶方法】两个功能下，共提供6个独立的模块来完成各种类型的方差分析。

以上内容摘自《SPSSAU科研数据分析方法与应用》第4章——差异关系研究，书中不仅涵盖了数据清理、统计分析和模型构建等内容，还提供了丰富的案例，以便于读者在实际研究中应用。