机器学习之神经网络学习

#Neural Network（神经网络）

• Non-linear hypothesis（非线性假设）

为什么需要神经网络？

• pixel（像素点）

只是包括平方项或者立方项特征，简单的logistic回归算法并不是一个在n很大的时候学习复杂的非线性假设的好方法，因为后者特征过多。

而神经网络在学习复杂的非线性假设上被证明是一种好得多的算法，即使输入的特征空间很大也能轻松搞定。

 

#神经网络的背景

• neuro-rewiring experiments（神经重接实验）

#Neurons and the brain（神经元与大脑）

• Axon（轴突）

 

#Model representation（模型展示）

单个神经元：

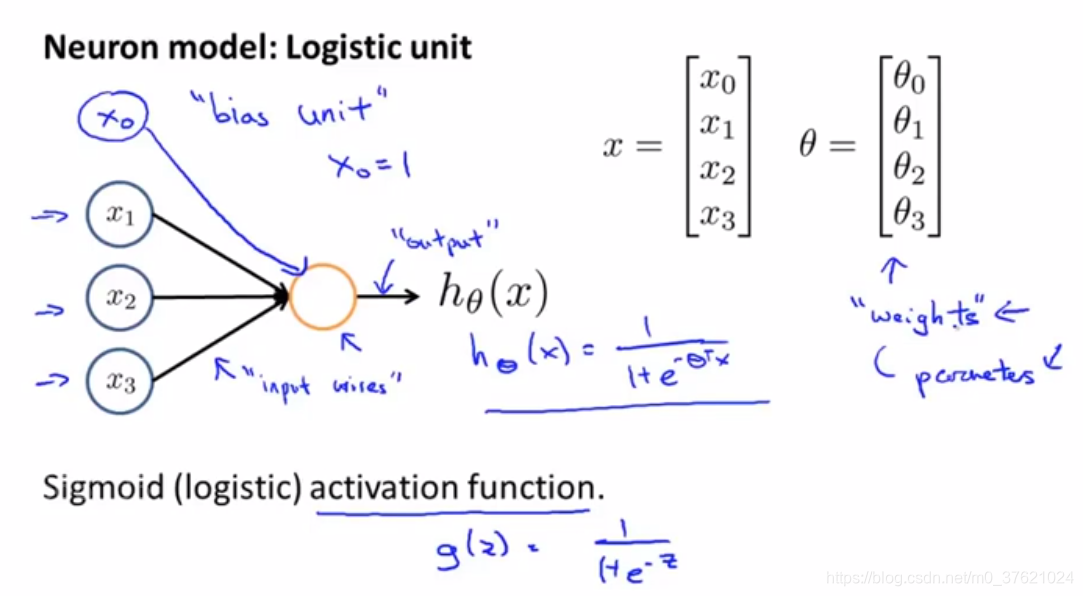
• x0有时被称作bias unit（偏置单元）或bias neuron（偏置神经元），通常为1。
• 模型参数θ也可称为weights of a model（模型的权重）

神经网络其实就是一组神经元连接在一起的集合：

• 网络中的第一层为input layer（输入层），在这边输入特征值；
• 中间的称为hidden layers（隐藏层），即非输出或输入层。
• 最后一层称为output layer（输出层），输出假设的最终计算结果。

从数学上定义神经网络的假设：

• activation（激活项）：由一个具体神经元计算并输出的值。

 

#forward propagation（前向传播）

从输入单元的激活项开始，然后进行前向传播给隐藏层，计算隐藏层的激活项，然后继续前向传播，并计算输出层的激活项。

而这一过程的vectorized implementation（向量化实现）方法：

 

神经网络做的事情就像逻辑回归，但是它不是使用原本的x1、x2...作为特征，而是用a1、a2...作为新的特征，它们是学习得到的函数输入值。神经网络是自己训练逻辑回归：

 

• architecture（神经网络架构）：神经网络中神经元的连接方式。

 

#例子和intuition（直观理解）

• XOR：当两个值恰好其中一个等于1时，这个式子为真。

神经网络所计算的逻辑函数的取值是怎样的？

• 逻辑和的功能：

• 逻辑或的功能：

• 逻辑非运算：在预期得到非结果的变量面前放一个很大的负权值。

@小思考：如何建立一个小规模的神经网络来计算这个逻辑函数【上图的（NOT x1）AND（NOT x2）】？

• 三个归在一起，计算XNOR函数：

 

这就是为什么神经网络可以计算这种复杂的函数，当网络拥有许多层，第二层有关于输入的相对简单的函数，第三层又在此基础上计算更加复杂的方程，再往后一层计算的函数越来越复杂：

 

#Multi-class classification（多类别分类问题）

采用的方法本质上是一对多法的拓展。

• training set（训练样本）：

 

---

PS.内容为学习吴恩达老师机器学习的笔记【https://study.163.com/course/introduction/1004570029.htm】