线性回归

线性回归

探究自变量与因变量之间的关系（只能是线性关系，不然就不叫线性回归了，233），且具有一定的预测能力。

为什么要具有预测能力？

因为人类想通过已有的数据，去预测未来

例如（用二维为例子）

有一些点，

x	y
0.5	1.5
1.5	2.5
2.5	3.5
3.5	4.5

让你通过这些点的关系（规律），来去预测当x=4.5的时候，y等于多少
如下图所示：

现在就是要探究自变量与因变量之间的关系，由于高中的知识加上数据十分完美以及观察点的规律，很容易得出，自变量与因变量之间属于线性关系，即可以用y=kx+b来表示所有的点，（我就不解方程了，蛤蛤）

得出y=x+1，这个就是，自变量与因变量之间的关系。
所以得出，当x=4.5的时候，y=4.5+1，也就是5.5

但是

实际的问题永远不会这么完美，也就是说，我观察到这些点的数据是这样的
另有一些点，

x	y
1	1.5
1.5	3
3	3
3.5	5

继续让你通过这些点的关系（规律），来去预测当x=4.5的时候，y等于多少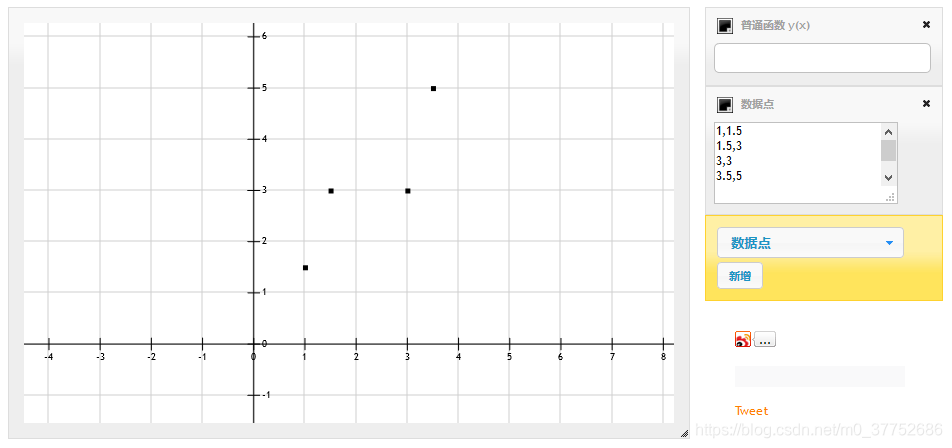
ok，继续探究自变量与因变量之间的关系，用到你所学的所有知识，你会发现，这些点，根本不可能用线性关系来去表示，也就是说，你找不到一条直线分别精确的过这4个点（不能用光滑的曲线来去把四个点连接起来，你确实可以找到这样的一条曲线过这四个点，但是这并不是线性回归，可以体会一下这个线性关系）

思路

那么这些点既然没有办法用一条线来去精确表示，那么就只能找到一条比较好的线，去近似或者最好的表示这些点的自变量与因变量之间的关系（找到X与Y的关系）。

问题就随之出现：

什么是最好的线？

在考虑这个问题的时候，前人给了我们2种方式，如果你可以想到如何判断这条线比较好，并且给出合理理由，你就伟大了，蛤蛤，在介绍这两种方式之前，用我的理解方式，需要一点前置的定义：

通过直线 y=kx+b 计算出来的值，我习惯叫理论上得到的值，写作：

题目中给定的点的y，也就是y真实的值，写作：

x	y
3.5	5

这里的y真实=5

---

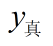
但是在上面也说过了，这条线，不可能经过所有的样本点，总是会有一些误差，也就是点要么在直线上面一点，要么在直线下面一点，于是就有了第一种判断这条线一个好的标准：

你也可以想一下，如果所有点到这条直线的距离都是0，也就是所有点都落在了这个直线上，是不是一个完美的线，但是找不到，于是放宽限制，这些不在直线上的点越接近这条直线，不就是最好的吗。

怎么表示点接近这条直线，那就只有点到直线的距离，

那如何表示一堆点是否接近这条直线，那就只有所有点到直线的距离累加和最小

所以按照思路，就会有：

所有点到直线的距离越小

但是有一点别忘了，点到直线的距离，是做垂线（可以转化），如下图所示

现在如果这条线，就是最好的线，也就是说，这里面几个点到直线的距离的累加和已经是最小的了。

这里由于直线的斜率是确定的（这个有空再证明。。TODO），所以，点到直线的距离最小可以转化为：

也就是函数值计算出来的y-y的真实值，这个整体要最小，为什么加绝对值，因为这样单纯相减可能出现负数，距离是没有负数的，所以要加绝对值。

但是在数学上，绝对值不好处理，比如求导，积分，都不喜欢绝对值。于是用平方来去改进式子：

即，所有点到直线的误差的平方和最小。

由于上次定义：

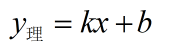
每个x点带入都会得到一个理论上的y
后面的y真实就是之前的样本点的y坐标

带入得以下公式：求这个公式的最小值

已知	未知
第i个样本的 $x_i$	斜率 k
第i个样本的 $y_i$	截距 b

---

如何求这个公式的最小值

最小二乘法