三体到底是啥？用Python跑一遍就明白了

温馨提示，只想看图请直接跳到最后一节

拉格朗日方程

此前所做的一切三体和太阳系的动画，都是基于牛顿力学的，而且直接对微分进行差分化，从而精度非常感人，用不了几年就得撞一起去。

为了给三体人提供一个更加有价值的推导，这次通过求解拉格朗日方程的数值解来实现。

首先假设三个质点的质量分别为$m_1,m_2,m_3$，坐标为${\vec{x}}_1,{\vec{x}}_2,{\vec{x}}_3$，质点速度可以表示为$\dot{\vec{x}}$。假设三体在二维平面上运动，则第$i$个质点的动能为

$$T_i=\frac{1}{2}{m}_i({\dot{x}}_i^2+{\dot{y}}_i^2)$$

引力势能为$-G\frac{m_i{m}_j}{r_{ij}}$，其中$G$为万有引力常量，$r_{ij}$为质点$i,j$之间的距离，则系统的拉格朗日量为

$$L=\sum _i\frac{1}{2}{m}_i({\dot{x}}_i^2+{\dot{y}}_i^2)-\sum _{i\ne j}G\frac{m_i{m}_j}{\Vert {\vec{x}}_i-{\vec{x}}_j\Vert }$$

有了拉格朗日量，将其带入拉格朗日方程

$$\frac{\text{d}}{\text{d}t}\frac{\partial L}{\partial {\dot{x}}_i}-\frac{\partial L}{\partial x_i}=0$$

就可以得到拉格朗日方程组。

推导方程组

对于三体系统而言，总计有3个粒子，每个粒子有$x,y$两个自由度，也就是说最后会得到6组方程。考虑到公式推导过程中可能会出现错误，所以下面采用sympy来进行公式推导。

首先定义符号变量

from sympy import symbols
from sympy.physics.mechanics import dynamicsymbols
m = symbols('m1:4')
x = dynamicsymbols('x1:4')
y = dynamicsymbols('y1:4')

接下来，需要构造系统的拉格朗日量$L$，其实质是系统的动能减去势能，对于上面构建的三体系统而言，动能和势能可分别表示为

计算每个质点的动能和势能。动能是由速度决定的，而速度是由位置对时间的导数决定的。我们可以用 sympy 的 diff 函数来求导：

from sympy import diff
# 此为速度的平方
v2 = [diff(x[i],t)**2 + diff(y[i])**2 for i in range(3)]
T = 0
for i in range(3):
    T += m[i]*v2[i]/2

势能是由万有引力决定的，而万有引力是由两个质点之间的距离决定的。我们可以用 sympy 的 sqrt 函数来求距离：

from sympy import sqrt,cos
G = symbols('G') # 引力常数
ijs = [(0,1), (0,2),(1,2)]
dij = [sqrt((x[i]-x[j])**2+(y[i]-y[j])**2) for i,j in ijs]
U = 0
for k in range(3):
    i,j = ijs[k]
    U -= G*m[i]*m[j]/dij[k]

有了动能和势能，就可以愉快地求拉格朗日量了，有了拉格朗日量，就可以列拉格朗日方程了

$$\begin{gathered} L=T-U \\ \frac{\text{d}L}{\text{d}{x}_i}-\frac{\text{d}}{\text{d}t}\frac{\partial L}{\partial {\dot{x}}_i} \end{gathered}$$

三个粒子的每一个坐标维度，都可以列出一组拉格朗日方程，所以总共有6个拉格朗日方程组

from sympy import solve
L = T - U
eqLag = lambda x : diff(L, x)-diff(diff(L, diff(x, t)), t)
# 拉格朗日方程组
eqs = [eqLag(xi) for xi in x+y]

记$x_{ij}=x_i-x_j,y_{ij}=y_i-y_j$，则

$$\begin{gathered} \frac{-G{m}_1{m}_2{x}_{12}}{{\left(x_{12}^2+y_{12}^2\right)}^{\frac{3}{2}}}+\frac{-G{m}_1{m}_3{x}_{13}}{{\left(x_{13}^2+y_{13}^2\right)}^{\frac{3}{2}}}-m_1\frac{d^2}{d{t}^2}{x}_1=0 \\ \frac{G{m}_1{m}_2{x}_{12}}{{\left(x_{12}^2+y_{12}^2\right)}^{\frac{3}{2}}}+\frac{-G{m}_2{m}_3{x}_{23}}{{\left(x_{23}^2+y_{23}^2\right)}^{\frac{3}{2}}}-m_2\frac{d^2}{d{t}^2}{x}_2=0 \\ \frac{G{m}_1{m}_3{x}_{13}}{{\left(x_{13}^2+y_{13}^2\right)}^{\frac{3}{2}}}+\frac{G{m}_2{m}_3{x}_{23}}{{\left(x_{23}^2+y_{23}^2\right)}^{\frac{3}{2}}}-m_3\frac{d^2}{d{t}^2}{x}_3=0 \\ \frac{-G{m}_1{m}_2{y}_{12}}{{\left(x_{12}^2+y_{12}^2\right)}^{\frac{3}{2}}}+\frac{-G{m}_1{m}_3{y}_{13}}{{\left(x_{13}^2+y_{13}^2\right)}^{\frac{3}{2}}}-m_1\frac{d^2}{d{t}^2}{y}_1=0 \\ \frac{G{m}_1{m}_2{y}_{12}}{{\left(x_{12}^2+y_{12}^2\right)}^{\frac{3}{2}}}+\frac{-G{m}_2{m}_3{y}_{23}}{{\left(x_{23}^2+y_{23}^2\right)}^{\frac{3}{2}}}-m_2\frac{d^2}{d{t}^2}{y}_2=0 \\ \frac{G{m}_1{m}_3{y}_{13}}{{\left(x_{13}^2+y_{13}^2\right)}^{\frac{3}{2}}}+\frac{G{m}_2{m}_3{y}_{23}}{{\left(x_{23}^2+y_{23}^2\right)}^{\frac{3}{2}}}-m_3\frac{d^2}{d{t}^2}{y}_3=0 \end{gathered}$$

微分方程算法化

接下来就要调用Python的odeint来计算这个微分方程组的数值解，odeint的调用方法大致为odeint(func, y, t, args)，其中func是一个函数，这个函数必须为func(y,t,...)，且返回值为$\frac{\text{d}y}{\text{d}t}$。

为此，需要将上述方程组再行拆分，以消去其中的二次导数，以$x_1$为例，令$u_1=\frac{\text{d}{x}_1}{\text{d}t}$，则此方程变为方程组

$$\begin{array}{rl}{\dot{x}}_1(t)& =u_1(t)\\ {\dot{u}}_1(t)& =\frac{-G{m}_1{m}_2{x}_{12}}{{\left(x_{12}^2+y_{12}^2\right)}^{\frac{3}{2}}}+\frac{-G{m}_1{m}_3{x}_{13}}{{\left(x_{13}^2+y_{13}^2\right)}^{\frac{3}{2}}}\end{array}$$

由于三体系统中有3个粒子，共6个独立变量，所以要列12个方程。记$u(t)=\frac{textdx}{\text{d}t},v(t)=\frac{\text{d}y}{\text{d}t}$，则odeint输入的y的形式为

$$[x_1,x_2,x_3,y_1,y_2,y_3,u_1,u_2,u_3,v_1,v_2,v_3]$$

从而func的具体形式为

import numpy as np
dxy = lambda x,y : np.sqrt(x**2+y**2)**(3/2)
def triSys(Y, t, m, G):
    jk = [(1,2),(0,2),(0,1)]
    x,y = Y[:3], Y[3:6]
    u,v = Y[6:9], Y[9:]
    du, dv = [], []
    for i in range(3):
        j, k = jk[i]
        xji, xki = x[j]-x[i], x[k]-x[i]
        yji, yki = y[j]-y[i], y[k]-y[i]
        dji, dki = dxy(xji, yji), dxy(yji, yki)
        mji, mki = G*m[i]*m[j], G*m[i]*m[k]
        du.append(mji*xji/dji + mki*xki/dki)
        dv.append(mji*yji/dji + mki*yki/dki)
    dydt = [*u, *v, *du, *dv]
    return dydt

求解+画图

接下来就是见证奇迹的时刻，首先创建一个随机的起点，作为三体运动的初值，然后带入开整就完事儿了

from scipy.integrate import odeint
np.random.seed(42)
y0 = np.random.rand(12)
m = np.random.rand(3)
t = np.linspace(0, 20, 1001)
sol = odeint(triSys, y0, t, args=(m, 1))

然后绘制一下这三颗星的轨迹

import matplotlib.pyplot as plt
plt.plot(sol[:,0], sol[:,3])
plt.plot(sol[:,1], sol[:,4])
plt.plot(sol[:,2], sol[:,5])
plt.show()

光是看这个轨迹就十分惊险了有木有。

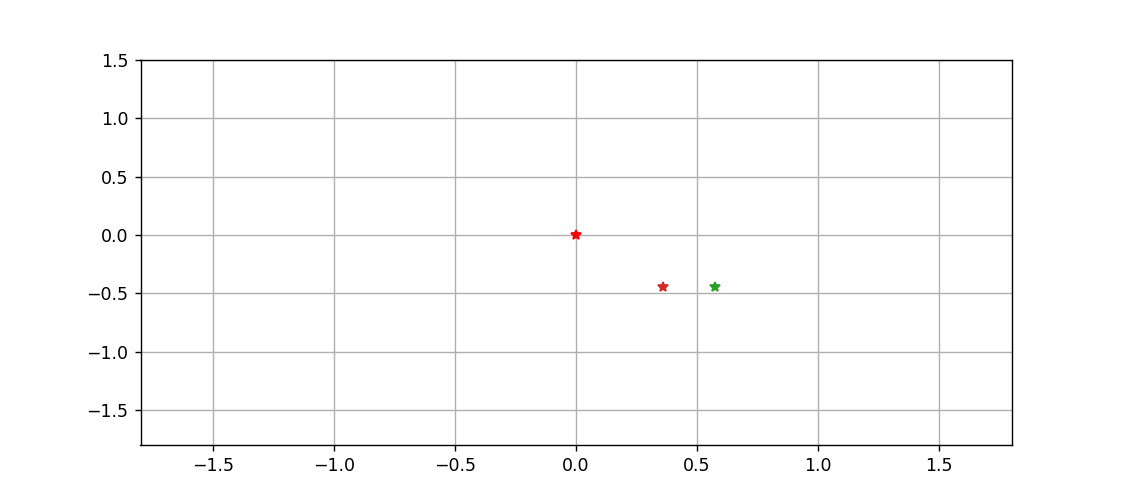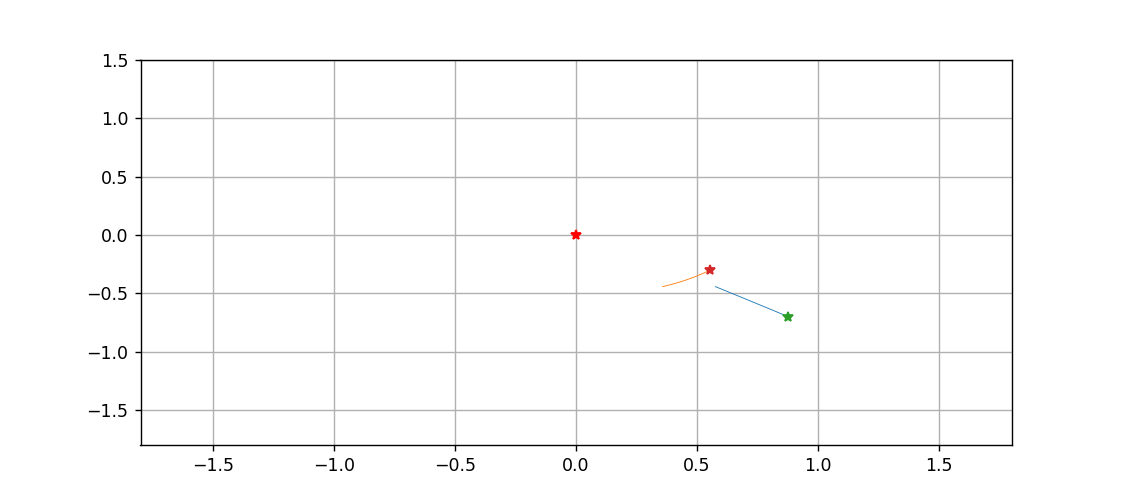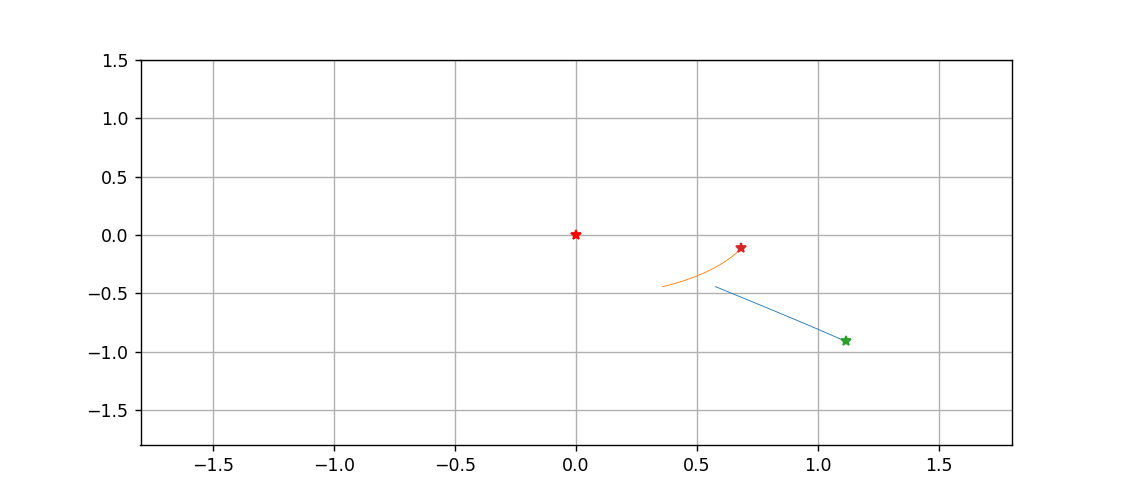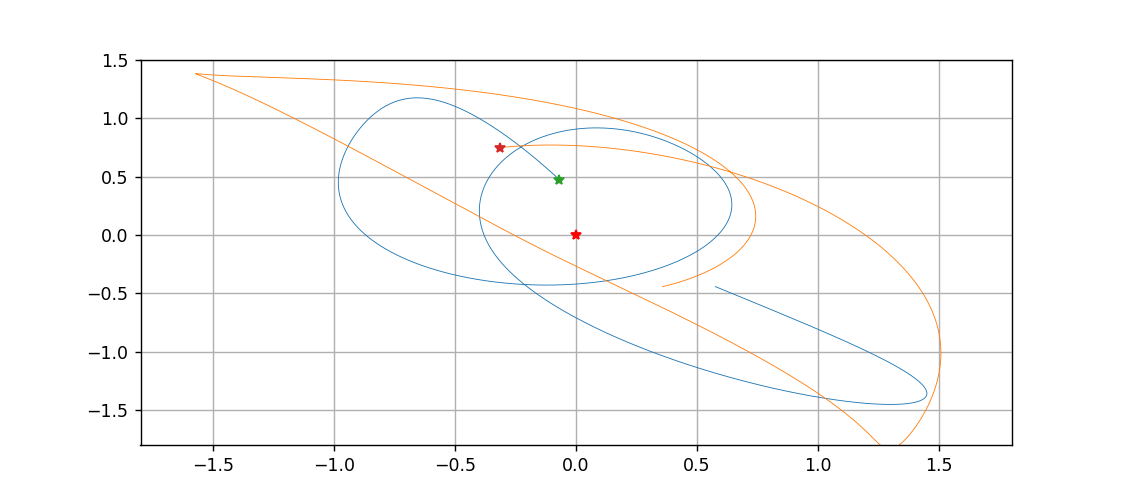
如果把其中的第一颗星作为坐标原点，那么另外两颗星的轨迹大致为

plt.plot(sol[:,1]-sol[:,0], sol[:,4]-sol[:,3])
plt.plot(sol[:,2]-sol[:,0], sol[:,5]-sol[:,3])
plt.scatter([0],[0], c='g', marker='*')
plt.show()

结果为

动图绘制

最后，以中间这颗星为原点，绘制一下另外两颗星运动的动态过程

import matplotlib.animation as animation 

fig = plt.figure(figsize=(9,4))
ax = fig.add_subplot(xlim=(-1.8,1.8),ylim=(-1.8,1.5))
ax.grid()

traces = [ax.plot([],[],'-',lw=0.5)[0] for _ in range(2)]
pts = [ax.plot([],[] ,marker='*')[0] for _ in range(2)]
ax.plot([0],[0], marker="*", c='r')

X1 = sol[:,1]-sol[:,0]
Y1 = sol[:,4]-sol[:,3]
X2 = sol[:,2]-sol[:,0]
Y2 = sol[:,5]-sol[:,3]

def animate(n):
    traces[0].set_data(X1[:n], Y1[:n])
    traces[1].set_data(X2[:n], Y2[:n])
    pts[0].set_data([X1[n], Y1[n]])
    pts[1].set_data([X2[n], Y2[n]])
    return traces + pts

ani = animation.FuncAnimation(fig, animate, 
    range(1000), interval=10, blit=True)
ani.save('tri.gif')