
数据集:
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
(
x
N
,
y
N
)
}
D=\{(x_1,y_1),(x_2,y_2),...(x_N,y_N)\}
D={(x1,y1),(x2,y2),...(xN,yN)}
样本:
x
i
∈
R
p
y
i
∈
R
x_i \in R^p \quad y_i \in R
xi∈Rpyi∈R
样本的矩阵表示:
X
=
(
x
1
,
x
2
,
.
.
.
,
x
N
)
T
Y
=
(
y
1
,
y
2
,
.
.
.
,
y
N
)
T
X=(x_1,x_2,...,x_N)^T \quad Y=(y_1,y_2,...,y_N)^T
X=(x1,x2,...,xN)TY=(y1,y2,...,yN)T
拟合函数:
f
(
w
)
=
W
T
X
f(w)=W^TX
f(w)=WTX
- 最小二乘角度:
损失函数:
L ( w ) = ∑ i = 1 N ( f ( w ) − y i ) 2 L(w) =\displaystyle\sum_{i=1}^N(f(w)-y_i)^2 L(w)=i=1∑N(f(w)−yi)2
= ∑ i = 1 N ( w T x i − y i ) 2 =\displaystyle\sum_{i=1}^N(w^Tx_i-y_i)^2 =i=1∑N(wTxi−yi)2
= ( w T x 1 − y 1 w T x 2 − y 2 . . . w T x N − y N ) ( w T x 1 − y 1 w T x 2 − y 2 . . . . . . . . . . . . . . w T x N − y N ) =(w^Tx_1-y_1 \quad w^Tx_2-y_2 \quad... \quad w^Tx_N-y_N) \left( \begin{array}{ccc} w^Tx_1-y_1 \\ w^Tx_2-y_2 \\ ..............\\ w^Tx_N-y_N \end{array} \right) =(wTx1−y1wTx2−y2...wTxN−yN)⎝⎜⎜⎛wTx1−y1wTx2−y2..............wTxN−yN⎠⎟⎟⎞
= { ( w T x 1 w T x 2 . . . w T x N ) − ( y 1 , y 2 , . . . , y N ) } ( w T x 1 − y 1 w T x 2 − y 2 . . . . . . . . . . . . . . w T x N − y N ) =\{(w^Tx_1 \quad w^Tx_2 \quad... \quad w^Tx_N)-(y_1,y_2,...,y_N)\} \left( \begin{array}{ccc} w^Tx_1-y_1 \\ w^Tx_2-y_2 \\ ..............\\ w^Tx_N-y_N \end{array} \right) ={(wTx1wTx2...wTxN)−(y1,y2,...,yN)}⎝⎜⎜⎛wTx1−y1wTx2−y2..............wTxN−yN⎠⎟⎟⎞
= { w T ( x 1 x 2 . . . x N ) − ( y 1 , y 2 , . . . , y N ) } ( w T x 1 − y 1 w T x 2 − y 2 . . . . . . . . . . . . . . w T x N − y N ) =\{w^T(x_1 \quad x_2 \quad... \quad x_N)-(y_1,y_2,...,y_N)\} \left( \begin{array}{ccc} w^Tx_1-y_1 \\ w^Tx_2-y_2 \\ ..............\\ w^Tx_N-y_N \end{array} \right) ={wT(x1x2...xN)−(y1,y2,...,yN)}⎝⎜⎜⎛wTx1−y1wTx2−y2..............wTxN−yN⎠⎟⎟⎞
=
(
w
T
X
T
−
Y
T
)
(
w
X
−
Y
)
=(w^TX^T-Y^T)(wX-Y)
=(wTXT−YT)(wX−Y)
展开函数:
=
w
T
X
T
w
X
−
Y
T
w
X
−
Y
w
T
X
T
+
Y
T
Y
=w^TX^TwX-Y^TwX-Yw^TX^T+Y^TY
=wTXTwX−YTwX−YwTXT+YTY
Y
T
w
X
和
Y
w
T
X
T
Y^TwX和Yw^TX^T
YTwX和YwTXT计算结果都是标量,可以进行合并
=
w
T
X
T
w
X
−
2
Y
w
T
X
T
+
Y
T
Y
=w^TX^TwX-2Yw^TX^T+Y^TY
=wTXTwX−2YwTXT+YTY
对w求偏导,并令导数为0有
∂
L
(
w
)
∂
w
=
2
X
T
X
W
−
2
X
T
Y
=
0
\frac{\partial L(w)}{\partial w}=2X^TXW-2X^TY=0
∂w∂L(w)=2XTXW−2XTY=0
X
T
X
W
=
X
T
Y
X^TXW=X^TY
XTXW=XTY
所以解析解为:
W
=
(
X
T
X
)
−
1
X
T
Y
W=(X^TX)^{-1}X^TY
W=(XTX)−1XTY
-
几何角度:
可以把 X = { x 1 , x 2 , . . . , x n } X=\{x_1,x_2,...,x_n\} X={x1,x2,...,xn}构成的矩阵看作一个子空间,那么显然, Y 构 成 的 向 量 不 在 该 列 空 间 中 Y构成的向量不在该列空间中 Y构成的向量不在该列空间中
那么也就是在X的列空间找到一个向量 v v v,使得 Y 到 X 的 距 离 最 短 Y到X的距离最短 Y到X的距离最短
根据投影知道: Y 到 子 空 间 X 的 投 影 距 离 是 最 短 的 Y到子空间X的投影距离是最短的 Y到子空间X的投影距离是最短的
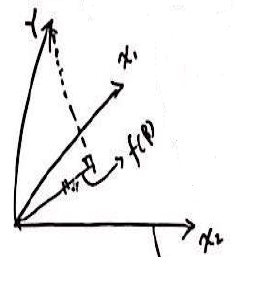
令:
X W 是 向 量 Y 在 X 上 面 的 投 影 , 则 有 : XW是向量Y在X上面的投影,则有: XW是向量Y在X上面的投影,则有:
X W − Y XW-Y XW−Y是X的正交补,从而有:
X T ( X W − Y ) = 0 X^T(XW-Y)=0 XT(XW−Y)=0
也就是
X T X W = X T Y X^TXW=X^TY XTXW=XTY
W = ( X T X ) − 1 X T Y W=(X^TX)^{-1}X^TY W=(XTX)−1XTY
可见和最小二乘计算结果一致 -
概率角度:
令
f ( x ) = w T x f(x)=w^Tx f(x)=wTx
y = f ( x ) + ε y = f(x) + \varepsilon y=f(x)+ε
ε ∼ N ( 0 , σ 2 ) \varepsilon \sim N(0,\sigma^2) ε∼N(0,σ2)
有:
y = w T x + ε y = w^Tx+ \varepsilon y=wTx+ε
所以 y 也 服 从 正 态 分 布 , 均 值 和 方 差 分 别 是 w T x , σ 2 y也服从正态分布,均值和方差分别是w^Tx,\sigma^2 y也服从正态分布,均值和方差分别是wTx,σ2
可以记作
y ∣ x , w ∼ N ( w T x , σ 2 ) y|x,w \sim N(w^Tx,\sigma^2) y∣x,w∼N(wTx,σ2)
对应的概率密度函数为
p ( y ∣ x , w ) = 1 2 π σ e x p ( − ( y i − w T x ) 2 2 σ 2 ) p(y|x,w) =\frac {1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^i-w^Tx)^2}{2\sigma^2}) p(y∣x,w)=2πσ1exp(−2σ2(yi−wTx)2)
对其应用对数似然函数有
L ( w ) = log P ( Y ∣ X , W ) = log ∏ i = 1 n p ( y ∣ x , w ) = ∑ 1 n log p ( y ∣ x , w ) L(w) = \log P(Y|X,W)=\log \prod_{i=1}^n p(y|x,w)=\sum_{1}^n \log p(y|x,w) L(w)=logP(Y∣X,W)=log∏i=1np(y∣x,w)=∑1nlogp(y∣x,w)
展开
L ( w ) = ∑ 1 n log 1 2 π σ e x p ( − ( y i − w T x ) 2 2 σ 2 ) L(w) =\sum_{1}^n \log \frac {1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^i-w^Tx)^2}{2\sigma^2}) L(w)=∑1nlog2πσ1exp(−2σ2(yi−wTx)2)
L ( w ) = ∑ 1 n ( log 1 2 π σ − ( y i − w T x ) 2 2 σ 2 ) L(w) =\sum_{1}^n (\log \frac {1}{\sqrt{2\pi}\sigma}-\frac{(y^i-w^Tx)^2}{2\sigma^2}) L(w)=∑1n(log2πσ1−2σ2(yi−wTx)2)
想要
a r g m a x ( L ( W ) argmax(L(W) argmax(L(W)
也就是
a r g m a x ( ∑ 1 n ( − ( y i − w T x ) 2 2 σ 2 ) ) argmax(\sum_{1}^n (-\frac{(y^i-w^Tx)^2}{2\sigma^2})) argmax(∑1n(−2σ2(yi−wTx)2))
也就是
a r g m i n ( ∑ 1 n ( y i − w T x ) 2 ) argmin(\sum_{1}^n (y^i-w^Tx)^2) argmin(∑1n(yi−wTx)2)
可以看到和最小二乘公式是一样的 -
带正则项的损失函数:
当样本数量较少时,容易出现过拟合问题
解决过拟合的几种办法
{ 增 加 数 据 选 取 特 征 、 或 者 降 维 ( P C A ) 正 则 化 \begin{cases} 增加数据 \\ 选取特征、或者降维(PCA) \\ 正则化 \end{cases} ⎩⎪⎨⎪⎧增加数据选取特征、或者降维(PCA)正则化
这里介绍两种基于线性回归的正则化方法
{ l a s s o 回 归 ( 1 范 数 ) r i d g e 回 归 ( 领 回 归 , 2 范 数 ) \begin{cases} lasso回归(1范数) \\ ridge回归(领回归,2范数) \\ \end{cases} {lasso回归(1范数)ridge回归(领回归,2范数)
带正则化的损失函数形式:
L
(
w
)
=
∑
i
=
1
N
(
f
(
w
)
−
y
i
)
2
+
λ
p
(
w
)
L(w) =\displaystyle\sum_{i=1}^N(f(w)-y_i)^2+\lambda p(w)
L(w)=i=1∑N(f(w)−yi)2+λp(w)
λ
p
(
w
)
称
作
惩
罚
项
\lambda p(w) 称作惩罚项
λp(w)称作惩罚项
这里以领回归为例:
=
w
T
X
T
X
w
−
2
Y
w
T
X
T
+
Y
T
Y
+
λ
w
T
w
=w^TX^TXw-2Yw^TX^T+Y^TY+\lambda w^Tw
=wTXTXw−2YwTXT+YTY+λwTw
=
w
T
(
X
T
X
+
λ
I
)
w
−
2
Y
w
T
X
T
+
Y
T
Y
=w^T(X^TX+\lambda I)w-2Yw^TX^T+Y^TY
=wT(XTX+λI)w−2YwTXT+YTY
对w求偏导有:
∂
L
(
w
)
∂
w
=
2
(
X
T
X
+
λ
I
)
w
−
2
X
T
Y
=
0
\frac{\partial L(w)}{\partial w}=2(X^TX+\lambda I)w-2X^TY=0
∂w∂L(w)=2(XTX+λI)w−2XTY=0
(
X
T
X
+
λ
I
)
w
=
X
T
Y
(X^TX+\lambda I)w=X^TY
(XTX+λI)w=XTY
所以解析解为:
W
=
(
X
T
X
+
λ
I
)
)
−
1
X
T
Y
W=(X^TX+\lambda I))^{-1}X^TY
W=(XTX+λI))−1XTY
- 贝叶斯角度:
假定:
f ( x ) = w t x f(x)=w^tx f(x)=wtx
y = w t x + ε y=w^tx+ \varepsilon y=wtx+ε
ε ∼ N ( 0 , σ 2 ) \varepsilon \sim N(0,\sigma^2) ε∼N(0,σ2)
w ∼ N ( 0 , σ 2 ) w \sim N(0,\sigma^2) w∼N(0,σ2)
所以有:
( y ∣ x , w ) ∼ N ( w t x , σ 2 ) (y|x,w) \sim N(w^tx,\sigma^2) (y∣x,w)∼N(wtx,σ2)
p ( y ∣ x , w ) = 1 2 π σ e x p ( − ( y i − w T x i ) 2 2 σ 2 ) p(y|x,w) =\frac {1}{\sqrt{2\pi}\sigma}exp(-\frac{(y_i-w^Tx_i)^2}{2\sigma^2}) p(y∣x,w)=2πσ1exp(−2σ2(yi−wTxi)2)
p ( w ) = 1 2 π σ e x p ( − w 2 2 σ 2 ) p(w) =\frac {1}{\sqrt{2\pi}\sigma}exp(-\frac{w^2}{2\sigma^2}) p(w)=2πσ1exp(−2σ2w2)
后验概率等于:
p ( w ∣ y ) = p ( y ∣ w ) p ( w ) p ( y ) p(w|y)=\displaystyle \frac{p(y|w)p(w)}{p(y)} p(w∣y)=p(y)p(y∣w)p(w)
最大化后验概率
M A P : w = a r g m a x p ( w ∣ y ) MAP: w=argmax \quad p(w|y) MAP:w=argmaxp(w∣y)
= a r g m a x p ( y ∣ w ) p ( w ) =argmax \quad p(y|w)p(w) =argmaxp(y∣w)p(w)
= a r g m a x ∏ i = 1 n 1 2 π σ e x p ( − ( y i − w T x i ) 2 2 σ 2 ) 1 2 π σ e x p ( − w 2 2 σ 2 ) =argmax \quad \displaystyle \prod_{i=1}^n\frac {1}{\sqrt{2\pi}\sigma}exp(-\frac{(y_i-w^Tx_i)^2}{2\sigma^2})\frac {1}{\sqrt{2\pi}\sigma}exp(-\frac{w^2}{2\sigma^2}) =argmaxi=1∏n2πσ1exp(−2σ2(yi−wTxi)2)2πσ1exp(−2σ2w2)
= a r g m a x ∏ i = 1 n 1 2 π σ 2 e x p ( − ( y i − w T x i ) 2 2 σ 2 − w 2 2 σ 2 ) =argmax \quad \displaystyle \prod_{i=1}^n\frac {1}{2\pi\sigma^2}exp(-\frac{(y_i-w^Tx_i)^2}{2\sigma^2}-\frac{w^2}{2\sigma^2}) =argmaxi=1∏n2πσ21exp(−2σ2(yi−wTxi)2−2σ2w2)
= a r g m a x ∑ i = 1 n { log 1 2 π σ 2 − ( ( y i − w T x i ) 2 2 σ 2 + w 2 2 σ 2 ) } =argmax \quad \displaystyle \sum_{i=1}^n\{ \log \frac {1}{2\pi\sigma^2}-(\frac{(y_i-w^Tx_i)^2}{2\sigma^2}+\frac{w^2}{2\sigma^2})\} =argmaxi=1∑n{log2πσ21−(2σ2(yi−wTxi)2+2σ2w2)}
= a r g m i n ∑ i = 1 n ( ( y i − w T x i ) 2 2 σ 2 + w 2 2 σ 2 ) =argmin \quad \displaystyle \sum_{i=1}^n(\frac{(y_i-w^Tx_i)^2}{2\sigma^2}+\frac{w^2}{2\sigma^2}) =argmini=1∑n(2σ2(yi−wTxi)2+2σ2w2)
= a r g m i n ∑ i = 1 n ( ( y i − w T x i ) 2 2 σ 2 + 1 2 σ 2 w 2 ) =argmin \quad \displaystyle \sum_{i=1}^n(\frac{(y_i-w^Tx_i)^2}{2\sigma^2}+\frac{1}{2\sigma^2}w^2) =argmini=1∑n(2σ2(yi−wTxi)2+2σ21w2)
可见和领回归公式是类似的























 4万+
4万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








