MCMC

概念：MCMC指的是马尔科夫链蒙特卡罗（Markov Chain Monte Carlo）
属于近似推断中的随机推断类别

1. 蒙特卡罗方法
   中心思想：用采样的平均值来代替求期望
   蒙特卡罗原来是一个赌场的名称，用它作为名字大概是因为蒙特卡罗方法是一种随机模拟的 方法，这很像赌博场里面的扔骰子的过程。最早的蒙特卡罗方法都是为了求解一些不太好求解的求和或者积分问题。比如积分：
   $\theta ={\int }_a^{b}f(x)dx$
   如果我们很难求解出f(x)的原函数，那么这个积分比较难求解。当然我们可以通过蒙特卡罗方法来模拟求解近似值。如何模拟呢？假设我们函数图像如下图:
   
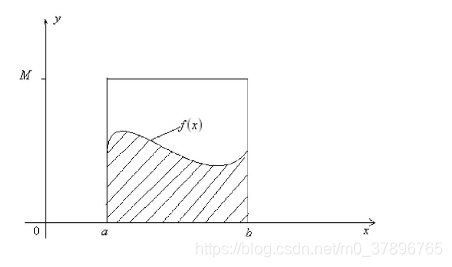
   则一个简单的近似求解方法是在[a,b]之间随机的采样一个点。比如$x_0$,然后用$f(x_0)$代表在[a,b]区间上所有的$f(x)$的值。那么上面的定积分的近似求解为:

$$(b-a)f(x_0)$$

当然，用一个值代表[a,b]区间上所有的$f(x)$的值，这个假设太粗糙。那么我们可以采样[a,b]区间的n个值：$x_0,x_1,...x_{n-1}$,用它们的均值来代表[a,b]区间上所有的$f(x)$的值。这样我们上面的定积分的近似求解为:

$$\frac{b-a}{n}\sum _{i=0}^{n-1}f(x_i)$$

虽然上面的方法可以一定程度上求解出近似的解，但是它隐含了一个假定，即$x$在[a,b]之间是均匀分布的，而绝大部分情况，$x$在[a,b]之间不是均匀分布的。如果我们用上面的方法，则模拟求出的结果很可能和真实值相差甚远。
怎么解决这个问题呢？ 如果我们可以得到$x$在[a,b]的概率分布函数$p(x)$，那么我们的定积分求和可以这样进行：
$$\theta ={\int }_a^{b}f(x)dx={\int }_a^b\frac{f(x)}{p(x)}p(x)dx\approx \frac{1}{n}\sum _{i=0}^{n-1}\frac{f(x_i)}{p(x_i)}$$

上式最右边的这个形式就是蒙特卡罗方法的一般形式。当然这里是连续函数形式的蒙特卡罗方法，但是在离散时一样成立。
可以看出，最上面我们假设$x$在[a,b]之间是均匀分布的时候，$p(x_i)=1/(b-a)$，带入我们有概率分布的蒙特卡罗积分的上式，可以得到：$$\frac{1}{n}\sum _{i=0}^{n-1}\frac{f(x_i)}{1/(b-a)}=\frac{b-a}{n}\sum _{i=0}^{n-1}f(x_i)$$
也就是说，我们最上面的均匀分布也可以作为一般概率分布函数$p(x)$在均匀分布时候的特例。那么我们现在的问题转到了如何求出$x$的分布$p(x)$对应的若干个样本上来。

采样方法：

• 概率分布采样
  上一节我们讲到蒙特卡罗方法的关键是得到$x$的概率分布。如果求出了$x$的概率分布，我们可以基于概率分布去采样基于这个概率分布的n个$x$的样本集，带入蒙特卡罗求和的式子即可求解。但是还有一个关键的问题需要解决，即如何基于概率分布去采样基于这个概率分布的n个$x$的样本集
  对于常见的均匀分布$uniform(0,1)$是非常容易采样样本的，一般通过线性同余发生器可以很方便的生成(0,1)之间的伪随机数样本。而其他常见的概率分布，无论是离散的分布还是连续的分布，它们的样本都可以通过$uniform(0,1)$的样本转换而得。比如二维正态分布的样本$(Z_1,Z_2)$可以通过通过独立采样得到的$uniform(0,1)$样本对$(X_1,X_2)$通过如下的式子转换而得：$$Z_1=\sqrt{-2ln{X}_1}cos(2\pi X_2)$$$$Z_2=\sqrt{-2ln{X}_1}sin(2\pi X_2)$$
  其他一些常见的连续分布，比如t分布，F分布，Beta分布，Gamma分布等，都可以通过类似的方式从$uniform(0,1)$得到的采样样本转化得到。在python的numpy，scikit-learn等类库中，都有生成这些常用分布样本的函数可以使用。
  不过很多时候，我们的$x$的概率分布不是常见的分布，这意味着我们没法方便的得到这些非常见的概率分布的样本集。那这个问题怎么解决呢？

• 接受-拒绝采样
  对于概率分布不是常见的分布，一个可行的办法是采用接受-拒绝采样来得到该分布的样本。既然 $p(x)$ 太复杂在程序中没法直接采样，那么我设定一个程序可采样的分布 $q(x)$ 比如高斯分布，然后按照一定的方法拒绝某些样本，以达到接近 $p(x)$ 分布的目的，其中$q(x)$叫做建议分布
  
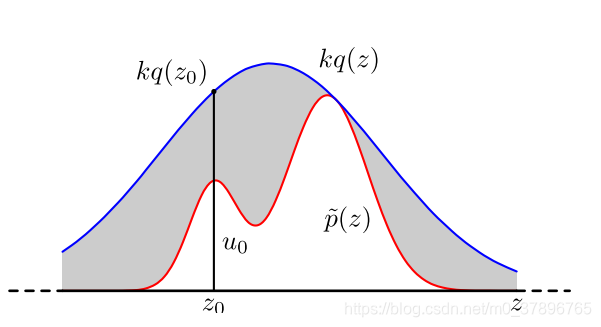
  具体操作如下，设定一个方便抽样的函数 q(x)，以及一个常量 k，使得 p(x) 总在 kq(x) 的下方。$\alpha =\frac{p(x)}{kq(x)}$（参考上图）

  • x 轴方向：从 q(x) 分布抽样得到 $z_0$。
  • y 轴方向：从均匀分布（0,1) 中抽样得到 u。
  • 如果$u\le \alpha$ 接受 $z_0$，否则拒绝
  • 重复以上过程
    在高维的情况下，Rejection Sampling 会出现两个问题，第一是合适的 q 分布比较难以找到，第二是很难确定一个合理的 k 值。这两个问题会导致拒绝率很高，无用计算增加。

• 重要性采样
  当 p(x)的分布比较好求解的时候，我们计算期望可以使用下列公式：
  $E[f(x)]={\int }_{x}p(x)f(x)dx$
  从$p(x)分布中采取N个样本，期望近似等于：$
  $E[f(x)]={\int }_{x}p(x)f(x)dx=\frac{1}{n}\sum _{i=1}^{n}f(x_i)$
  但是当$p(x)比较复杂，无法从p(x)中采集样本的时候，我们引入一个建议分布q(x),能够从这个分布中采集样本：$
  $E[f(x)]={\int }_{x}p(x)f(x)dx={\int }_x\frac{p(x)q(x)}{q(x)}f(x)dx$
  $={\int }_{x}q(x)f(x)\frac{p(x)}{q(x)}dx$
  我们能够从$q(x)采集若干样本，有下列式子成立$
  $=\frac{1}{n}\sum _{i=1}^{n}f(x_i)\frac{p(x)}{q(x)}$
  其中的$\frac{p(x)}{q(x)}$ 称为权重(weight)

2.马氏链及其平稳分布
数学定义：$P(X_{t+1}=x|X_t,X_{t-1},\cdots )=P(X_{t+1}=x|X_t)$
也就是状态转移的概率只依赖于前一个状态

我们先来看马氏链的一个具体的例子。社会学家经常把人按其经济状况分成 3 类：下层 (lower-class)、中层 (middle-class)、上层 (upper-class)，我们用 1、2、3 分别代表这三个阶层。社会学家们发现决定一个人的收入阶层的最重要的因素就是其父母的收入阶层。如果一个人的收入属于下层类别，那么他的孩子属于下层收入的概率是 0.65，属于中层收入的概率是 0.28，属于上层收入的概率是 0.07。事实上，从父代到子代，收入阶层的变化的转移概率如下

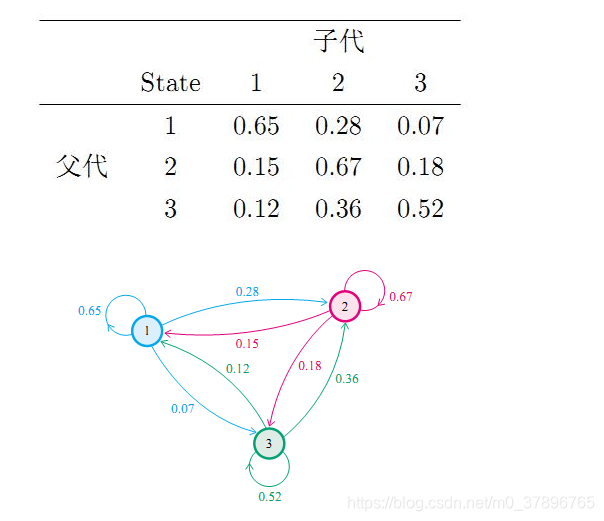
使用矩阵的表示方式，转移概率矩阵记为:
$$P=\left[\begin{array}{ccc}0.65& 0.28& 0.07\\ 0.15& 0.67& 0.18\\ 0.12& 0.36& 0.52\end{array}\right]$$
假设当前这一代人处在下层、中层、上层的人的比例是概率分布向量
${\pi }_0=[{\pi }_0(1),{\pi }_0(2),{\pi }_0(3)]$
那么他们的子女的分布比例将是${\pi }_1={\pi }_{0}P$
他们的孙子代的分布比例将是${\pi }_2={\pi }_{1}P={\pi }_0{P}^2$
……,
第 n代子孙的收入分布比例将是 ${\pi }_n={\pi }_{n-1}P={\pi }_0{P}^n$
假设初始概率分布为${\pi }_0=[0.21,0.68,0.11]$,则我们可以计算前 n代人的分布状况如下:

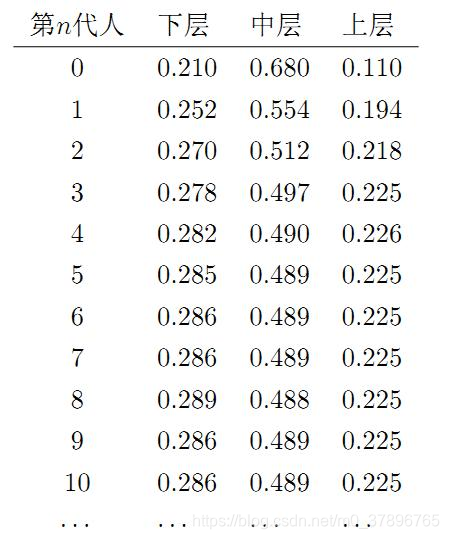
我们发现从第 7 代人开始，这个分布就稳定不变了，这个是偶然的吗？我们换一个初始概率分布${\pi }_0=[0.75,0.15,0.1]$试试看，继续计算前 n代人的分布状况如下:

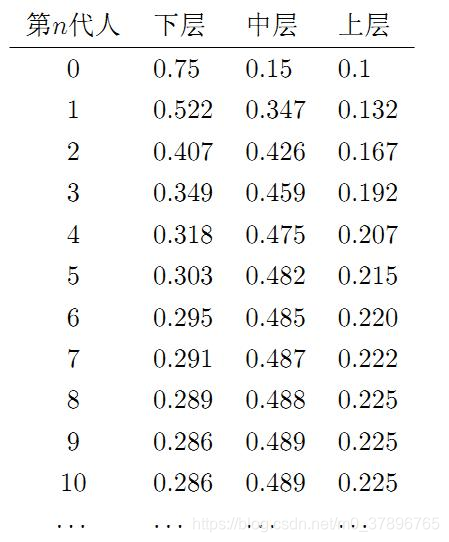
我们发现，到第 9 代人的时候, 分布又收敛了。最为奇特的是，两次给定不同的初始概率分布，最终都收敛到概率分布 $\pi =[0.286,0.489,0.225]$,也就是说收敛的行为和初始概率分布
${\pi }_0$无关,这说明这个收敛行为主要是由概率转移矩阵 $P$决定的。我们计算一下$P^n$
$$P^{20}=P^{21}=\cdots =P^{100}=\cdots =\left[\begin{array}{ccc}0.286& 0.489& 0.225\\ 0.286& 0.489& 0.225\\ 0.286& 0.489& 0.225\end{array}\right]$$
我们发现，当n足够大的时候，这个$P^n$ 矩阵的每一行都是稳定地收敛到
$\pi =[0.286,0.489,0.225]$这个概率分布,这个收敛现象并非是我们这个马氏链独有的，而是绝大多数马氏链的共同行为，关于马氏链的收敛我们有如下漂亮的定理：
马氏链定理： 如果一个非周期马氏链具有转移概率矩阵$P$且它的任何两个状态是连通的
那么$\underset{n\to \infty }{\lim }{P}_{ij}^n$存在且与 i 无关，
记$\underset{n\to \infty }{\lim }{P}_{ij}^n=\pi (j)$ ,我们有
$$1:\underset{n\to \infty }{\lim }{P}^n=\left[\begin{array}{ccccc}\pi (1)& \pi (2)& \cdots & \pi (j)& \cdots \\ \pi (1)& \pi (2)& \cdots & \pi (j)& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \pi (1)& \pi (2)& \cdots & \pi (j)& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right]$$
$$2:\pi (j)=\sum _{i=0}^{\infty }\pi (i)P_{ij}$$
$3:\pi 是方程\pi P=\pi 的唯一非负解,其中：$
$$\pi =[\pi (1),\pi (2),\cdots ,\pi (j),\cdots ],\sum _{i=0}^{\infty }{\pi }_i=1$$
$\pi$称为马氏链的平稳分布
这个马氏链的收敛定理非常重要，所有的 MCMC(Markov Chain Monte Carlo) 方法都是以这个定理作为理论基础的。定理的证明相对复杂，一般的随机过程课本中也不给证明，所以我们就不用纠结它的证明了，直接用这个定理的结论就好了。我们对这个定理的内容做一些解释说明：

• 该定理中马氏链的状态不要求有限，可以是有无穷多个的,因此可以用于连续概率分布和离散概率分布；
• 非周期的马尔科夫链：这个主要是指马尔科夫链的状态转化不是循环的，如果是循环的则永远不会收敛。幸运的是我们遇到的马尔科夫链一般都是非周期性的
• 任何两个状态是连通的：这个指的是从任意一个状态可以通过有限步到达其他的任意一个状态，不会出现条件概率一直为0导致不可达的情况
• π 通常称为马尔科夫链的平稳分布。

3. Markov Chain Monte Carlo
对于给定的概率分布 $p(x)$我们希望能有便捷的方式生成它对应的样本。由于马氏链能收敛到平稳分布， 于是一个很的漂亮想法是：如果我们能构造一个转移矩阵为$P$的马氏链，使得该马氏链的平稳分布恰好是 $p(x)$,那么我们从任何一个初始状态 $x_0$ 出发沿着马氏链转移, 得到一个转移序列 $x_0,x_1,x_2,\cdots x_n,x_{n+1}\cdots$
如果马氏链在第 n步已经收敛了，于是我们就得到了 $\pi (x)的样本x_n,x_{n+1},...$
由上一节的例子和定理我们看到了，马氏链的收敛性质主要由转移矩阵 P决定, 所以基于马氏链做采样的关键问题是如何构造转移矩阵 P, 使得平稳分布恰好是我们要的分布 $p(x)$如何能做到这一点呢？我们主要使用如下的定理:
定理：[细致平稳条件] 如果非周期马氏链的转移矩阵 $P$和分布 $\pi (x)$ 满足:
$$\pi (i)P_{ij}=\pi (j)P_{ji}\text{for all}i,j$$
则 $\pi (x)$是马氏链的平稳分布，上式被称为细致平稳条件 (detailed balance condition)。
即满足马尔可夫链的收敛性质。
也就是说，只要我们找到了可以使概率分布$\pi (x)$满足细致平稳分布的矩阵P即可。这给了我们寻找从平稳分布$\pi (x)$, 找到对应的马尔科夫链状态转移矩阵P的新思路。

不过不幸的是，仅仅从细致平稳条件还是很难找到合适的矩阵P。比如我们的目标平稳分布是$\pi (x)$,随机找一个马尔科夫链状态转移矩阵Q,它是很难满足细致平稳条件的，即：
$$\pi (i)Q(i,j)\ne \pi (j)Q(j,i)$$
那么如何使这个等式满足呢？下面我们来看MCMC采样如何解决这个问题。
由于一般情况下，目标平稳分布$\pi (x)$和某一个马尔科夫链状态转移矩阵Q不满足细致平稳条件，即:
$$\pi (i)Q(i,j)\ne \pi (j)Q(j,i)$$
我们可以对上式做一个改造，使细致平稳条件成立。方法是引入一个α(i,j),使上式可以取等号，即：
$$\pi (i)Q(i,j)\alpha (i,j)=\pi (j)Q(j,i)\alpha (j,i)$$
问题是什么样的α(i,j)可以使等式成立呢？其实很简单，按照对称性，只要满足下两式即可：
$$\alpha (i,j)=\pi (j)Q(j,i)$$
$$\alpha (j,i)=\pi (i)Q(i,j)$$
所以有：
$$p(i)\underset{Q^{\prime }(i,j)}{\underbrace{Q(i,j)\alpha (i,j)}}=p(j)\underset{Q^{\prime }(j,i)}{\underbrace{Q(j,i)\alpha (j,i)}}(\ast \ast )$$
于是我们把原来具有转移矩阵 $Q$ 的一个很普通的马氏链,改造为了具有转移矩阵$Q^{{}^{\prime }}$ 的马氏链，而 $Q^{{}^{\prime }}$恰好满足细致平稳条件，由此马氏链 $Q^{{}^{\prime }}$ 的平稳分布就是$p(x)$ ！
在改造 $Q$ 的过程中引入的 $\alpha (i,j)$称为接受率,物理意义可以理解为在原来的马氏链上，从状态i以$Q(i,j)$的概率转跳转到状态 j的时候,我们以 $\alpha (i,j)$的概率接受这个转移，于是得到新的马氏链$Q^{{}^{\prime }}$的的转移概率为$Q(i,j)\alpha (i,j)$

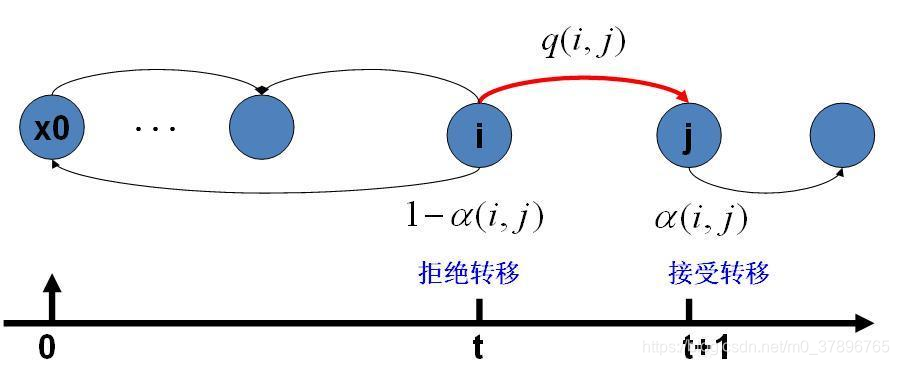
马氏链转移和接受概率

假设我们已经有一个转移矩阵 Q(对应元素为 $q(i,j)$), 把以上的过程整理一下，我们就得到了如下的用于采样概率分布 $p(x)$的算法。

上述过程中 $p(x).q(x|y)$说的都是离散的情形，事实上即便这两个分布是连续的，以上算法仍然是有效，于是就得到更一般的连续概率分布$p(x)$的采样算法，而 $q(x|y)$就是任意一个连续二元概率分布对应的条件分布。

以上的 MCMC 采样算法已经能很漂亮的工作了，不过它有一个小的问题：马氏链 Q在转移的过程中的接受率 $\alpha (i,j)$可能偏小，这样采样过程中马氏链容易原地踏步，拒绝大量的跳转，这使得马氏链遍历所有的状态空间要花费太长的时间，收敛到平稳分布 $p(x)$ 的速度太慢。有没有办法提升一些接受率呢?

M-H采样
M-H采样是Metropolis-Hastings采样的简称，这个算法首先由Metropolis提出，被Hastings改进，因此被称之为Metropolis-Hastings采样或M-H采样

M-H采样解决了我们上一节MCMC采样接受率过低的问题。

我们回到MCMC采样的细致平稳条件：
$$\pi (i)Q(i,j)\alpha (i,j)=\pi (j)Q(j,i)\alpha (j,i)$$
我们采样效率低的原因是α(i,j)太小了，比如为0.1，而α(j,i)为0.2。即：
$$\pi (i)Q(i,j)\times 0.1=\pi (j)Q(j,i)\times 0.2$$
这时我们可以看到，如果两边同时扩大五倍，接受率提高到了0.5，但是细致平稳条件却仍然是满足的，即：
$$\pi (i)Q(i,j)\times 0.5=\pi (j)Q(j,i)\times 1$$
这样我们的接受率可以做如下改进，即：
α ( i , j ) = m i n { π ( j ) Q ( j , i ) π ( i ) Q ( i , j ) , 1 } \alpha(i,j) = min\{ \frac{\pi(j)Q(j,i)}{\pi(i)Q(i,j)},1\} α(i,j)=min{π(i)Q(i,j)π(j)Q(j,i)​,1}
于是，经过对上述 MCMC 采样算法中接受率的微小改造，我们就得到了如下教科书中最常见的 Metropolis-Hastings 算法。

4: Gibbs Sampling
对于高维的情形，由于接受率 α的存在 (通常 α<1)，以上 Metropolis-Hastings 算法的效率不够高。能否找到一个转移矩阵 Q 使得接受率 α=1呢？我们先看看二维的情形，假设有一个概率分布
p(x,y)， 考察 $x$ 坐标相同的两个点 A(x1,y1),B(x1,y2)，我们发现
$$\begin{gathered} p(x_1,y_1)p(y_2|x_1)=p(x_1)p(y_1|x_1)p(y_2|x_1) \\ p(x_1,y_2)p(y_1|x_1)=p(x_1)p(y_2|x_1)p(y_1|x_1) \end{gathered}$$
所以有：
$p(x_1,y_1)p(y_2|x_1)=p(x_1,y_2)p(y_1|x_1)(\ast \ast \ast )$
即：
$p(A)p(y_2|x_1)=p(B)p(y_1|x_1)$
基于以上等式，我们发现，在 x=x1这条平行于 y轴的直线上，如果使用条件分布$p(y|x1)$
做为任何两个点之间的转移概率，那么任何两个点之间的转移满足细致平稳条件。同样的，如果我们在 y=y1这条直线上任意取两个点 A(x1,y1),C(x2,y1)，也有如下等式:
$p(A)p(x_2|y_1)=p(C)p(x_1|y_1).$

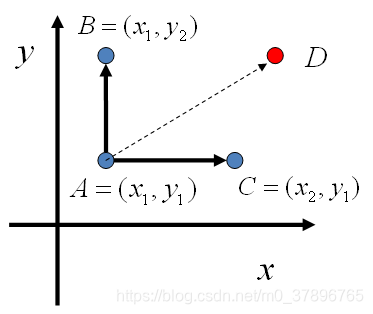
平面上马氏链转移矩阵的构造

于是我们可以如下构造平面上任意两点之间的转移概率矩阵 Q
$$\begin{array}{rlrl}Q(A\to B)& =p(y_B|x_1)& \text{如果}{x}_A=x_B=x_1& \\ Q(A\to C)& =p(x_C|y_1)& \text{如果}{y}_A=y_C=y_1& \\ Q(A\to D)& =0& \text{其它}& \end{array}$$
有了如上的转移矩阵 Q，我们很容易验证对平面上任意两点 X,Y， 满足细致平稳条件
$p(X)Q(X\to Y)=p(Y)Q(Y\to X)$
这个算法就称为 Gibbs Sampling 算法

多维Gibbs采样
上面的这个算法推广到多维的时候也是成立的。比如一个n维的概率分布$\pi (x_1,x_2,...x_n)$
我们可以通过在n个坐标轴上轮换采样，来得到新的样本。对于轮换到的任意一个坐标轴xi上的转移，马尔科夫链的状态转移概率为
$P(x_i|x_1,x_2,...,x_{i-1},x_{i+1},...,x_n)$即固定n−1个坐标轴，在某一个坐标轴上移动。

轮换坐标轴不是必须的，我们可以随机选择某一个坐标轴进行状态转移，只不过常用的Gibbs采样的实现都是基于坐标轴轮换的。

参考资料
https://cosx.org/2013/01/lda-math-mcmc-and-gibbs-sampling
https://www.cnblogs.com/pinard/p/6645766.html