padding、空洞对图片分辨率大小的影响

目录

1.padding的概念

2.感受野的概念

3.图片大小不变，padding多少？

4.空洞率对应的卷积核尺寸及其感受野大小

5.空洞卷积后图片大小变化

---

1.padding的概念

为什么padding？

卷积操作存在的两个问题：

1. 图像越来越小
2. 图像边界信息丢失，即有些图像角落和边界的信息发挥作用较少

因此需要padding

• padding的操作就是在图像块的周围加上格子，从而使得图像经过卷积过后大小不会变化，这种操作是使得图像的边缘数据也能被利用到，这样才能更好的扩张整张图像的边缘特征。
• padding是在卷积之前补0。
• padding补0的策略是四周都补；如果padding=1，那么就会在原来输入层的基础上，上下左右各补一行。
• padding的用途：保持边界信息；可以对有差异的图片进行补齐，使得图像的输入大小一致。

2.感受野的概念

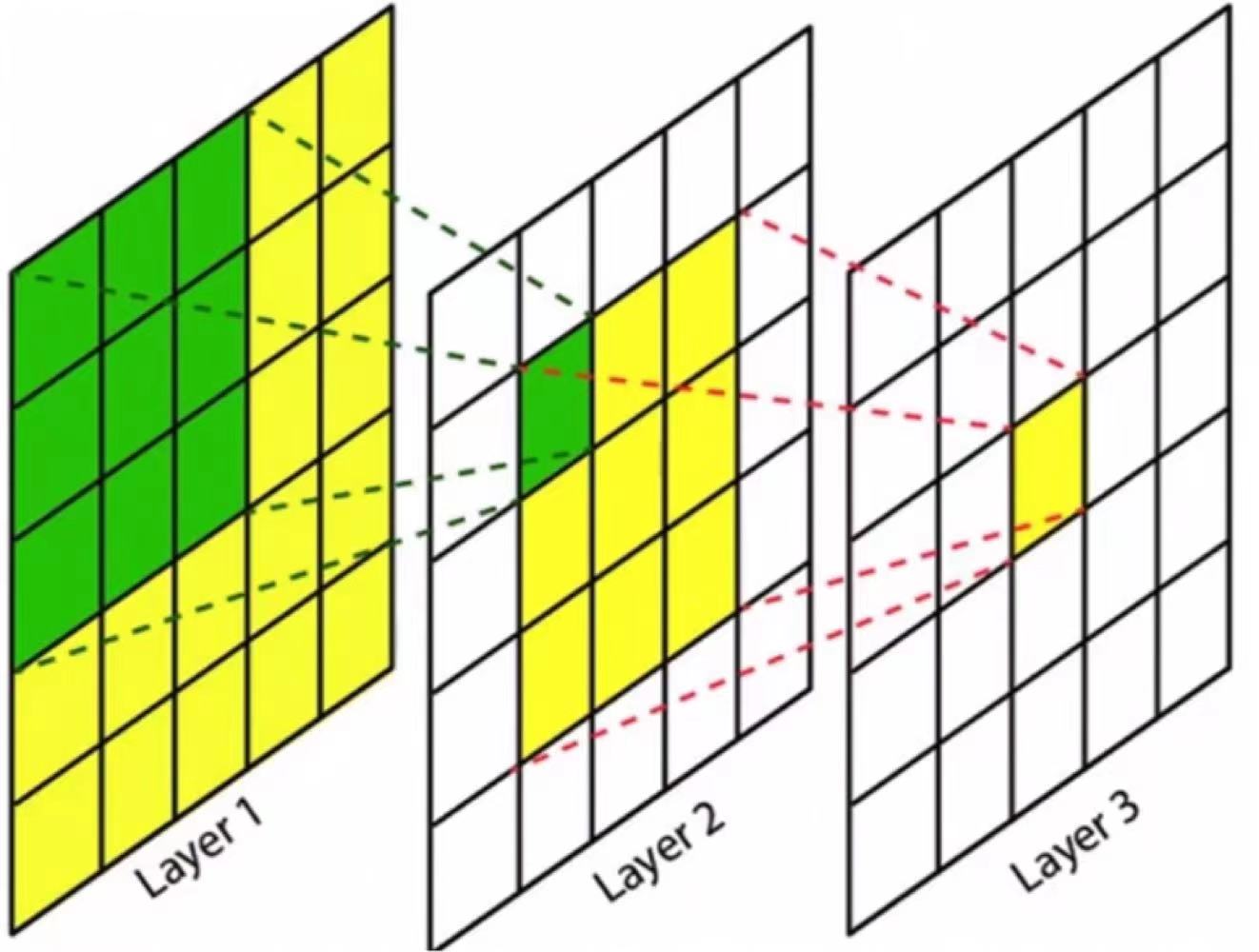
在卷积神经网络中，决定某一层输出结果中一个元素所对应的输入层的区域大小（注意是对应输入层，而不是前一层），被称作感受野。通常来说，大感受野的效果要比小感受野的效果更好。由公式可见，stride越大，感受野越大。但是过大的stride会使feature map保留的信息变少。因此，在减少stride的情况下，如何增大感受野或使其保持不变，称为分割任务中的一大问题。

如下图所示，layer2的感受野相对于输入层layer1为3×3；layer3的感受野相对于输入层layer1为5×5。

3.图片大小不变，padding多少？

这里有一个问题：假设输入图像的分辨率为H×W，卷积核为k×k，stride为1，问若要保持卷积前后分辨率大小不变，padding应该设为多少？

先给出答案：padding = （k-1）// 2

那这个答案是怎么来的呢？

我们知道卷积后图片分辨率大小的计算公式

我们使，则得出

4.空洞率对应的卷积核尺寸及其感受野大小

感受野及卷积核的计算公式如下所示：

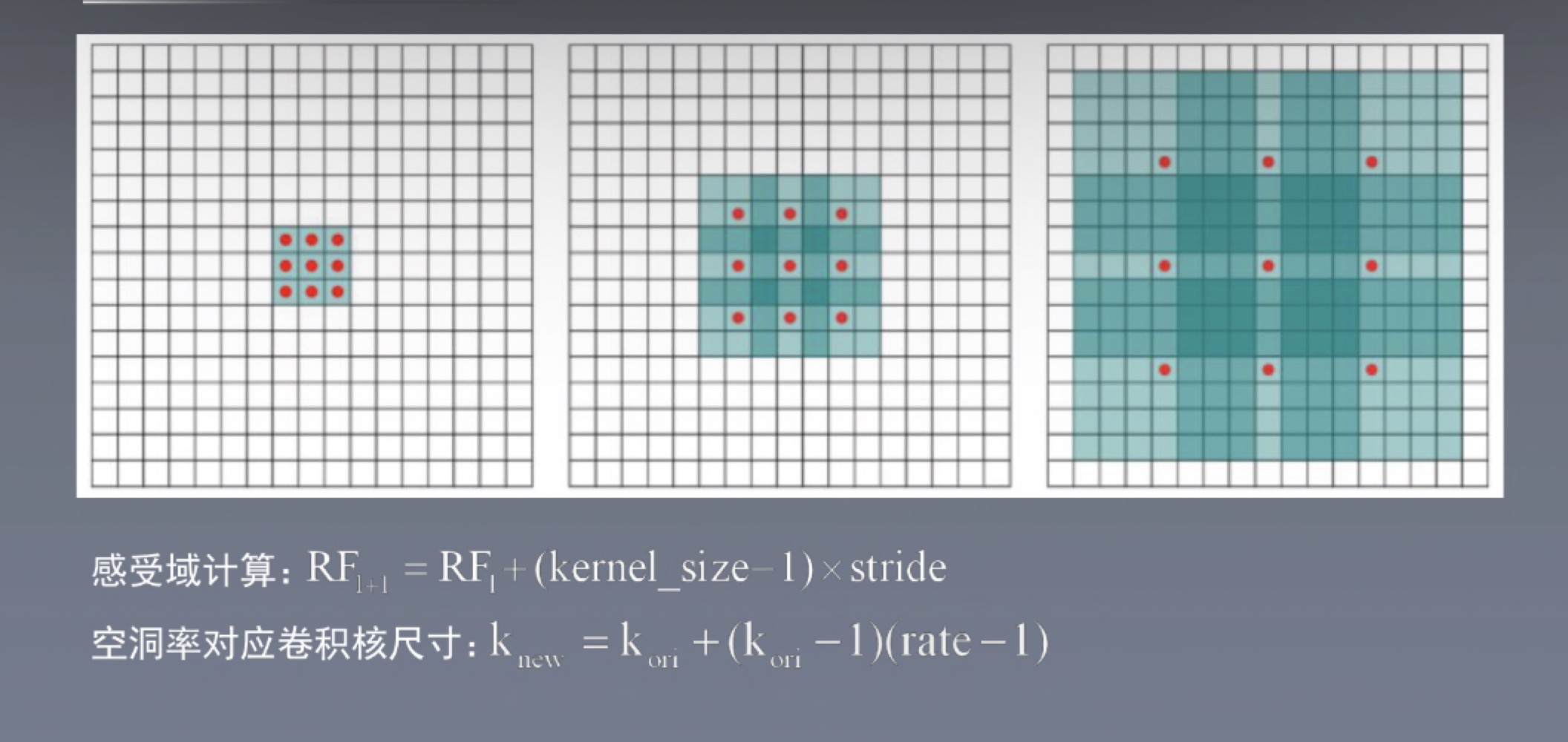
我们将上图三个空洞率分别1,2,4的卷积核大小及感受野大小计算一下（绿色部分为感受野大小，红点为卷积核大小）：

左图（rate = 1）：

• rate = 1的卷积核即为标准卷积，卷积核尺寸为3×3，感受域为3×3

中图（rate = 2）：

• 卷积核大小为：
• 感受野大小为：

右图（rate = 4）：

• 卷积核大小为：
• 感受野大小为：

5.空洞卷积后图片大小变化

标准卷积图片分辨率计算公式：

而空洞卷积只需要将K替换为

所以空洞卷积图片分辨率计算公式：