【题解】P2685 [TJOI2012]桥（最短路，dijkstra，multiset）

最新推荐文章于 2024-07-15 22:10:26 发布

Sunflower_ac

最新推荐文章于 2024-07-15 22:10:26 发布

阅读量161

点赞数

文章标签：算法

本文链接：https://blog.csdn.net/m0_46222454/article/details/126309504

版权

【题解】P2685 [TJOI2012]桥

挺妙的一道题。这里提供一种不用线段树的做法。

题目链接

P2685 [TJOI2012]桥 - 洛谷

题意概述

给定一张 \(n\) 个点 \(m\) 条边的无向图。求把这张图上任意一条边断掉后，形成的新的从 \(1\) 到 \(n\) 的最短路最大是多少，并输出满足最大值的方案数。

思路分析

首先，只有断掉最短路上的边时，才会对最后的最短路长度有影响；如果炸的不是最短路上的边，就对最短路长度没有影响。

那么我们分类讨论：

若原图上断掉最短路上的边后形成的新的最短路的最大值仍然与原最短路长度相同，那么说明这张图上断掉任意一条边都可以(不一定是最短路上边)，那么方案数就是边数 \(m\)；
若原图上断掉最短路上的边后形成的新的最短路的最大值大于原最短路长度，那么就只能断掉原最短路上符合要求的边；
稍微思考可知，断掉最短路上的边后形成的新的最短路的最大值不可能小于原最短路长度。

那么我们现在只需要计算在断掉最短路上的任意一条边后形成的新的最短路最大值是多少。

首先考虑一个结论：

假设原图最短路上有 \(s\) 个点，最短路径为 \(1-v_1-v_2-v_3-\cdots-v_s\)，那么在最短路上炸掉一条边 \(v_i \rightarrow v_{i+1}\) 之后，所形成的新的最短路一定是 \(1-v_1-v_2-\cdots -v_j-一些非最短路上的边-v_k-\cdots -v_s(j\le i,k \ge i+1)\)。

换句话说，在最短路上删掉一条边 \((u,v)\) 后，我们怎么走才能让路径继续最短呢？一定是从起点沿着原来的最短路走到 \(u\) 及 \(u\) 之前的某个点，偏离最短路，走不在原来最短路上的边，到达 \(v\) 及 \(v\) 之后的某个点，再沿着原来的最短路走完。

这里有点抽象我们画个图理解一下。

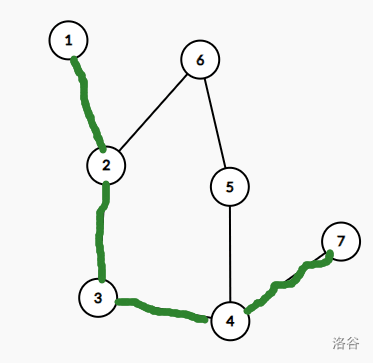
(此图仅供理解方便，实际上不符合题意，原题是边双。)

假设原最短路是 \(1 \rightarrow 2 \rightarrow 3\rightarrow 4\rightarrow 7\) (图中标绿的路径)，若断掉边 \(3\rightarrow4\)，那么新的最短路就只能从在最短路上的 \(3\) 或者 \(3\) 之前“偏离”最短路，在 \(4\) 或者 \(4\) 之后回到最短路。

在这张图中只能是 \(1 \rightarrow 2 \rightarrow 6 \rightarrow 5\rightarrow 4 \rightarrow 7\)。

这个结论很好证明，以上图中，除了被断掉的地方其它地方必须经过最短路，这样才能保证“最短”。

这个结论告诉我们：我们在新的最短路上走时，最多只能“偏离”原最短路一次，“回到”原最短路一次。

你是否联想到什么呢？

这不就相当于，一架飞机，从起点走到终点，在中间只能起飞一次，降落一次，而我们关注的就是起飞的时机和降落的时机使得最后走的路程最小。

那么我们可以先考虑，把原最短路找出来，然后考虑对于每条非最短路上的边，如果我让飞机必须经过这条边，那它在什么时候起飞，在什么时候降落。

现在的问题就是先找到原图的最短路。

那么我们可以考虑在之前见到过的好多题用的技巧：

跑两遍 dijkstra，分别预处理出来从 \(1\) 出发到每个点 \(i\) 的最短路 \(dis1_i\) 以及从 \(n\) 出发到每个点 \(i\) 最短路 \(dis2_i\)。

然后我们利用 \(dis2\) 这个数组标记出来最短路上的所有边并对他们重新编号。

具体做法：从 \(1\) 开始，枚举当前节点 \(now\) 的每条出边 \(nxt\)，如果 \(now\) 到 \(n\) 的距离等于 \(now \rightarrow nxt\) 这条边的边权加上 \(nxt\) 到 \(n\) 的距离，那么这条边在最短路上，将它标记出来。

那么有人会问了，那如果一个图有多个最短路怎么办呢？

实际上我们只需要标记出来其中一条即可，原因如下：

\(1\) 到 \(n\) 的最短路，如果有多个，那么就是说最短路某边上两点 \((u,v)\) 之间，还有一条别的长度相等的路径，那么我们若断掉 \((u,v)\) 这条边，完全可以走另外一条路径，所以不影响。

这部分求解代码如下：

for(int now=1;now!=n;)
{
	for(Node nxt:edge[now])
	{
		if(dis2[nxt.v]+nxt.w==dis2[now])
		{
			now=nxt.v;
			book[nxt.id]++;
			break;
		}
	}
}

在标记完原最短路后，我们就可以维护两个数组 \(l\) 和 \(r\)：

\(l_u\) 表示第一个不在 \(1 \rightarrow u\) 最短路上的边的编号；

\(r_u\) 表示最后一个不在 \(u \rightarrow n\) 最短路上的边的编号。

比如对于上面那张图，我们对于边编个号：

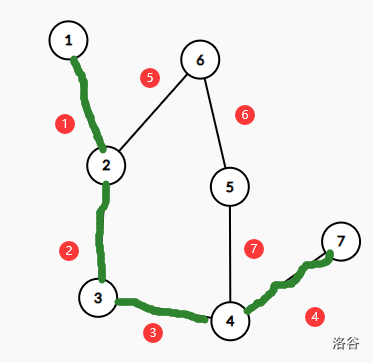
在这张图中：

\(l_2=2,r_2=1,l_6=2,r_6=3,\cdots\)

我们暂且先不管 \(l\) 和 \(r\) 是怎么求的，来考虑一下如何利用 \(l\) 和 \(r\) 求解问题。

其实这里的 \(l\) 和 \(r\) 对标的是在飞机起飞降落模型中的起飞时机和降落时机。

那么我们现在要知道的就是：对于每一条非原最短路上的边(即图中的绿边)，什么时候要通过这条边以及这条边所在最短路径的长度是多少。

以上图为例，假如我们要通过 ⑤ 号边，那么只有当 ② 或 ③ 被断开时，才能经过它。

我们发现，假如要经过一条非原最短路的边 \(u \rightarrow v\)，只有当 \(l_u\) 到 \(r_v\) 中有个桥断了，我们才会考虑走这条边，此时形成的新的最短路长度就为 \(dis1_u+w(u,v)+dis2_v\)。其中 \(w(u,v)\) 表示从 \(u\) 到 \(v\) 这条边的边权。

等等，假如 \(u=6,v=2\) 呢？那么应该是 \(l_v\) 到 \(r_u\) 喽？实际上这是另一种走向，一种从 \(2 \rightarrow 6\)，一种是 \(6 \rightarrow 2\)。

所以当 \(l_u \le r_v\) 时，我们新的最短路长度为 \(dis1_u+w(u,v)+dis2_v\)；

当 \(l_v \le r_u\) 时，新的最短路长度为 \(dis1_v+w(u,v)+dis2_u\)。

注意：这两个条件并不对立，可以并存也可以均不满足。

我们用两个 basic_string：

\(dp1_i\) 表示的是飞机在边 \(i-1\) 的终点“起飞”所能形成的路径的集合；

\(dp2_i\) 表示的是飞机在边 \(i+1\) 的起点“降落”所能形成的路径的集合。

维护每次计算的路径长度。

这部分代码如下：

for(int i=1;i<=m;i++)
{
	if(book[i])continue;
	int u=e[i].u,v=e[i].v,w=e[i].w;
    if(l[u]<=r[v])
	{
		dp1[l[u]]+=dis1[u]+w+dis2[v];
		dp2[r[v]]+=dis1[u]+w+dis2[v];
	}
	if(l[v]<=r[u])
	{
		dp1[l[v]]+=dis1[v]+w+dis2[u];
		dp2[r[u]]+=dis1[v]+w+dis2[u];
	}
}

然后我们考虑原最短路上的每一条边，每一条边被断掉后，相当于飞机从这个点前起飞，降落到这个点之后。

考虑我们 \(l\) 和 \(r\) 数组的本质：\(l_i\) 表示的是从 \(i-1\) 开始之后任意断哪一条边都行，\(r_i\) 表示的是从 \(i+1\) 往前任意断哪一条边都行，那么这两个的交集，就表示从 \(1\) 到 \(l_i+1\)，从 \(r_i+1\) 到 \(n\) 的所有的边都不能断。

可以考虑用 multiset 来维护。

我们从左到右枚举每一个最短路上的边 \(i\)，每次枚举刚开始将 \(dp1_i\) 中的所有元素加入一个 multiset 中维护，然后取最小值，就是当前在 \(i\) 之前起飞在 \(i\) 之后降落的最小距离。

需要注意的一点是，在每次枚举结束之前，需要将 \(dp2_i\) 中的元素从 multiset 中移除，为什么呢？

因为 \(dp2_i\) 表示的是在 \(i+1\) 的起点降落，也就是说一定会经过 \(i+1\) 这条边，而我们枚举的下一个是断掉 \(i+1\) 这条边，所以 \(dp2_i\) 一定是不符合下一次枚举的条件的，所以必须要移除。

这里可能有点抽象，我们再借助图理解一下：

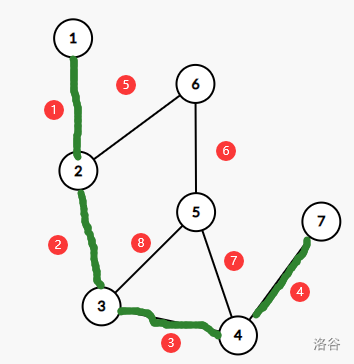
假设我们在上面那张图的 \(3\) 和 \(5\) 之间再连一条边，编号为 ⑧，那么对于路径 \(1 \rightarrow 2 \rightarrow 6 \rightarrow 5 \rightarrow 3 \rightarrow 4 \rightarrow 7\)，我们会在枚举边 ② 时加入到 multiset 中，由于它在 \(3\) 号节点就回到了原最短路上，所以我们在枚举边 ③ 时就不能把它算进去，是不合法的。

最后统计一下方案数就好。

这部分代码如下：

int cnt=0;//方案数； 
for(int i=1;i<=tot;i++)
{
	for(int tt:dp1[i])ss.insert(tt);
	if(*ss.begin()>ans){ans=*ss.begin();cnt=1;}
	else if(*ss.begin()==ans)cnt++;
	for(int tt:dp2[i])ss.erase(ss.find(tt));
} 
if(ans==dis1[n])cnt=m;//这里在刚开始分析思路的时候就已经解释过了。断掉最短路上的边后不影响最短路长度。
cout<<ans<<" "<<cnt<<endl;

最后我们来考虑如何求 \(l\) 和 \(r\) 数组。

首先由于 \(l_u\) 是当前最小的不在 \(1-u\) 最短路上的编号，所以我们要将 \(l\) 数组初始化为无穷大，同理要将 \(r\) 初始化为 \(0\)。

然后对于原最短路上的每个点 \(u\)，它的 \(l\) 设为从 \(u\) 到 \(n\) 最短路径上第一条边的编号，\(r\) 设为从 \(1\) 到 \(u\) 路径上最后一条边的编号。

这个很好理解。

那么对于非原最短路上点来说，如何求出它的 \(l\) 和 \(r\) 呢？

先以 \(l\) 为例，我们可以将所有的点按照到 \(1\) 的最短路长度从小到大排序，然后枚举每一个不是最短路上的点，用它的 \(l\) 来更新与它连边的所有点的 \(l\)，这里有点类似于 dijkstra 的“松弛”操作，具体做法：设当前点为 \(now\)，与它连边的点是 \(nxt\)，若 \(now\) 在 \(1\) 到 \(nxt\) 的最短路上且 \(l_{nxt}>l_{now}\)，那么就用 \(l_{now}\) 来更新 \(l_{nxt}\)

聪明的小伙伴就会发现，这实际上也相当于也跑了一遍 dijkstra。

之所以要按照 \(dis1\) 从小到大排序，这实际上就是满足了一种拓扑排序，这块相当于是一个 DP，我们必须保证用距离 \(1\) 更近的节点的 \(l\) 去更新距离 \(1\) 更远的答案，也相当于 dijkstra 中每次从小根堆出取出堆顶。如果不排序，那么就相当于拓扑排序中，一个节点的入度没有减为 \(0\) 就入队了，这有可能导致答案错误。

而之所以必须满足 \(l_{nxt}>l_{now}\) 才能更新答案，我们继续借助上面的图理解一下。

假设 \(now=6,nxt=5\)，此时的 \(l_5=3\)，那么由于 \(l_6=2 < l_5\)，所以用 \(l_6\) 更新 \(l_5\)。这就相当于你找到了飞机起飞的更早的时间，而由于我们的 \(l\) 数组的含义是最小的不在 \(1\) 到当前节点路径上的边，所以要用 \(l_6\) 更新 \(l_5\)，就是这个意思。

求 \(r\) 与求 \(l\) 同理，这里不再赘述。

这部分代码如下：

for(int i=1;i<=n;i++)z[i]=i;
sort(z+1,z+n+1,cmp1);
for(int i=1;i<=n;i++)
{
	int now=z[i];
	for(Node nxt:edge[now])
	{
		if(book[nxt.id])continue;
		if(dis1[nxt.v]==dis1[now]+nxt.w&&l[nxt.v]>l[now])l[nxt.v]=l[now];
	}
}
sort(z+1,z+n+1,cmp2);
for(int i=1;i<=n;i++)
{
	int now=z[i];
	for(Node nxt:edge[now])
	{
		if(book[nxt.id])continue;
		if(dis2[nxt.v]==dis2[now]+nxt.w&&r[nxt.v]<r[now])r[nxt.v]=r[now];
	}
}

到此为止，这道题的所有思路就全部分析完了。

回过头来看这道题，实际上相当于跑了四遍 dijkstra，两遍分别用来求从 \(1\) 出发的最短路和从 \(n\) 出发的最短路，两遍用来求 \(l\) 和 \(r\)。而这四个数组，正是这道题的关键所在。

另外还有一个 multiset，这道题的所有题解都是用线段树维护了这个操作，但在这种解法中，提供了一个不用线段树只有简单的 STL 就解决问题的办法。很妙。

不得不说，这是一道最短路好题，让我更加深刻的认识到了 dijkstra 一些本质的东西，甚至也帮我理解了 DP 中的一些东西，同时让我更加理解了 multiset 的用法，受益匪浅。

代码实现

//luoguP2685
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<set>
#define int long long
using namespace std;
const int maxn=1e5+10;
int dis1[maxn],dis2[maxn],vis[maxn],vis2[maxn];
int l[maxn],r[maxn],z[maxn],book[maxn<<1];
int n,m;
int ans;

struct Node{
    int v,w,id;
    bool operator<(const Node &t)const
    {
    	return w>t.w;
	}
};

struct nod{int u,v,w;}e[maxn<<1];

basic_string<Node>edge[maxn];
basic_string<int>dp1[maxn],dp2[maxn];
multiset<int>ss;

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

void dijkstra1()
{
	priority_queue<Node>q;
	for(int i=1;i<=n;i++)dis1[i]=(1ll<<31)-1;
	dis1[1]=0;int tt=0;
	q.push(Node{1ll,dis1[1],tt});
	while(!q.empty())
	{
		Node now=q.top();
		q.pop();
		if(vis[now.v])continue;
		vis[now.v]++;
		for(Node y:edge[now.v])
		{
			if(dis1[y.v]>dis1[now.v]+y.w)
			{
				dis1[y.v]=dis1[now.v]+y.w;
				q.push(Node{y.v,dis1[y.v],tt});
			}
		}
	}
}

void dijkstra2()
{
	priority_queue<Node>q;
	for(int i=1;i<=n;i++)dis2[i]=(1ll<<31)-1;
	int s=n;
	dis2[n]=0;int tt=0;
	q.push(Node{s,dis2[s],tt});
	while(!q.empty())
	{
		Node now=q.top();
		q.pop();
		if(vis2[now.v])continue;
		vis2[now.v]++;
		for(Node y:edge[now.v])
		{
			if(dis2[y.v]>dis2[now.v]+y.w)
			{
				dis2[y.v]=dis2[now.v]+y.w;
				q.push(Node{y.v,dis2[y.v],tt});
			}
		}
	}
}

int cmp1(int a,int b){return dis1[a]<dis1[b];}
int cmp2(int a,int b){return dis2[a]<dis2[b];}

signed main()
{
	n=read();m=read();
	for(int i=1;i<=m;i++)
	{
		int s,t,c;
		s=read();t=read();c=read();
		e[i].u=s;e[i].v=t;e[i].w=c;
		edge[s]+=Node{t,c,i};
		edge[t]+=Node{s,c,i};
	}
	//正反跑两遍 dij。预处理出来所有点到 1 和 n 的最短路。 
	dijkstra1();
	dijkstra2();
	//初始化 l 和 r。并标记所有当前最短路上的点。 
	memset(l,0x3f3f3f,sizeof(l)); 
	l[1]=1;
	int tot=0;
	for(int now=1;now!=n;)
	{
		for(Node nxt:edge[now])
		{
			if(dis2[nxt.v]+nxt.w==dis2[now])
			{
				now=nxt.v;
				book[nxt.id]++;
				break;
			}
		}
		r[now]=++tot;
		l[now]=tot+1;
	}
	//求每一个 l 和 r。 
	for(int i=1;i<=n;i++)z[i]=i;
	sort(z+1,z+n+1,cmp1);
	for(int i=1;i<=n;i++)
	{
		int now=z[i];
		for(Node nxt:edge[now])
		{
			if(book[nxt.id])continue;
			if(dis1[nxt.v]==dis1[now]+nxt.w&&l[nxt.v]>l[now])l[nxt.v]=l[now];
		}
	}
	sort(z+1,z+n+1,cmp2);
	for(int i=1;i<=n;i++)
	{
		int now=z[i];
		for(Node nxt:edge[now])
		{
			if(book[nxt.id])continue;
			if(dis2[nxt.v]==dis2[now]+nxt.w&&r[nxt.v]<r[now])r[nxt.v]=r[now];
		}
	}
	//求出对于每一条非原最短路边，哪一条最短路边删掉之后这条边才有用。
	for(int i=1;i<=m;i++)
	{
		if(book[i])continue;
		int u=e[i].u,v=e[i].v,w=e[i].w;
		if(l[u]<=r[v])
		{
			dp1[l[u]]+=dis1[u]+w+dis2[v];
			dp2[r[v]]+=dis1[u]+w+dis2[v];
		}
		if(l[v]<=r[u])
		{
			dp1[l[v]]+=dis1[v]+w+dis2[u];
			dp2[r[u]]+=dis1[v]+w+dis2[u];
		}
	 } 
	//求出删掉每一条原最短路边后对应的答案。
	int cnt=0;//方案数； 
	for(int i=1;i<=tot;i++)
	{
		for(int tt:dp1[i])ss.insert(tt);
		if(*ss.begin()>ans){ans=*ss.begin();cnt=1;}
		else if(*ss.begin()==ans)cnt++;
		for(int tt:dp2[i])ss.erase(ss.find(tt));
	 } 
	if(ans==dis1[n])cnt=m;
	cout<<ans<<" "<<cnt<<endl;
	return 0;
}

Sunflower_ac

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【题解】P2685 [TJOI2012]桥（最短路，dijkstra，multiset）

【题解】P2685 [TJOI2012]桥挺妙的一道题。这里提供一种不用线段树的做法。题目链接P2685 [TJOI2012]桥 - 洛谷题意概述给定一张 \(n\) 个点 \(m\) 条边的无向图。求把这张图上任意一条边断掉后，形成的新的从 \(1\) 到 \(n\) 的最短路最大是多少，并输出满足最大值的方案数。思路分析首先，只有断掉最短路上的边时，才会对最后的最短路长度有影响...
复制链接

扫一扫