因子图基础知识学习（isam）

m0_46254725

已于 2023-09-13 22:22:59 修改

阅读量2.1k

点赞数 18

分类专栏：因子图文章标签：学习算法

于 2023-09-13 11:11:40 首次发布

本文链接：https://blog.csdn.net/m0_46254725/article/details/132848059

版权

因子图专栏收录该内容

3 篇文章 0 订阅

订阅专栏

文章目录

因子图求解中转换

笔记来源：深蓝学院，董靖公开课 www.shenlanxueyuan.com/open/course/28

因子图求解中转换

1、非线性最小二乘共性问题

因子图的优化目标是图中所有状态参数变量，使得所有观测因子的连乘结果最大，每个因子认为服从高斯分布。问题描述如下：
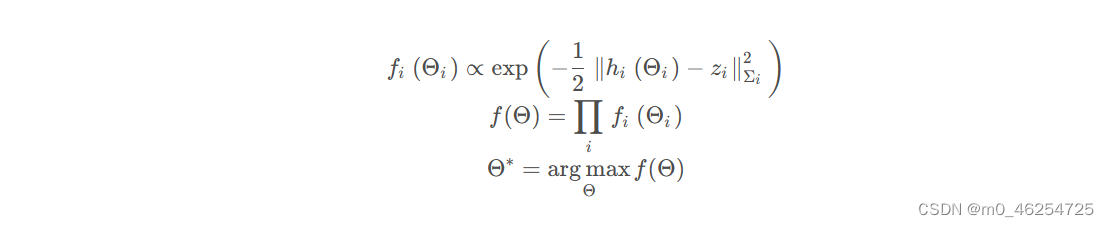
在这里插入图片描述
将问题的目标函数在初始的参数位置进行线性化得到如下表达式：

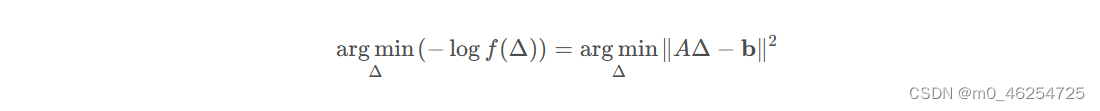
这样就将非线性最小二乘问题转化成了线性最小二乘问题，注意到其中的：

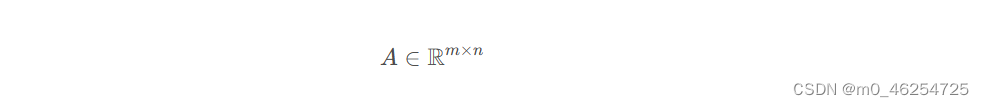
m为测量行 n为变量数，对于因子图问题每多一个新的状态量一定会多至少一个因子，因此m总是大于n的。A是长条形的，因此对A进行QR分解得到:
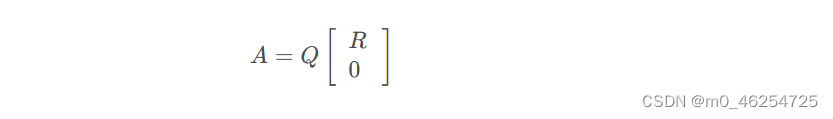
在这里插入图片描述
最小二乘问题化简成：

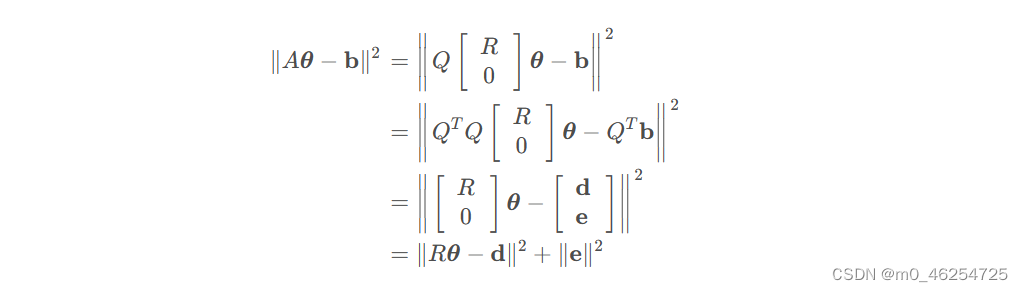
后半部分为常数部分，前半部分为二次型，最小值为零，因此最小二乘问题被转换成上式前半部分的线性方程组的解。
增量式因子图构建与问题求解

2、因子图→

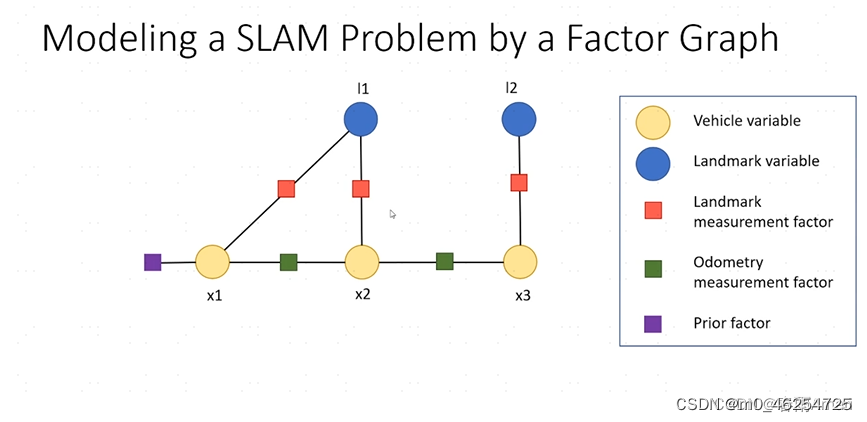
在这里插入图片描述
圈：表示状态量
方块：表示观测量，也就是因子
先验因子：

对于上面的因子图，我们用下面的式子来描述：
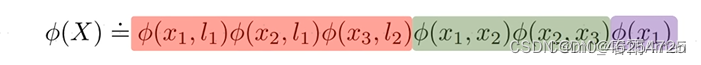
在这里插入图片描述
其中红色的部分表示观测因子，绿色为里程计因子，紫色为先验因子。那我们要解决的问题是什么呢，就是寻找一个最优的X，使得这些因子图的乘积最大化。

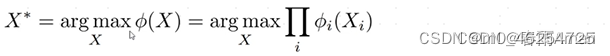
因子图中每个因子的定义：在因子图中通常每个因子都是通过指数函数的形式来定义的，这是因为我们得到的观测量是有不确定性的，而且现实中这种不确定性通常服从高斯分布：（因为每个因子描述的是观测值，大部分符合高斯分布，这里使用指数形式）
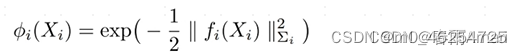
在这里插入图片描述
其中f(x)表示误差函数，误差越小，f(x)越小，指数函数越大，X*越大

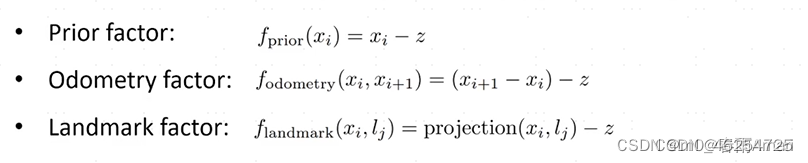
3、→非线性最小二乘问题

目标：求解这个最优化问题，
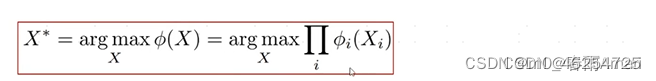
在这里插入图片描述
对于目标函数的右边取负对数，可将

最大化X*=最大化因子的乘积问题→转化成一个非线性最小二乘问题：

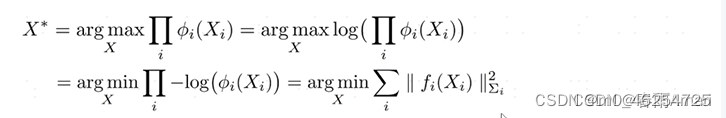
在这里插入图片描述

4、→线性最小二乘问题

使用高斯牛顿迭代法求解

首先给定X一个初始值（通常在slam问题中这个初始值我们使用上一时刻得到的最有状态估计X），在给定这个变量的基础上再去求一个修改量，最后在用这个初始值加上这个修改量得到新的状态X，重复迭代这个过程，直到收敛。其流程如下图所示：
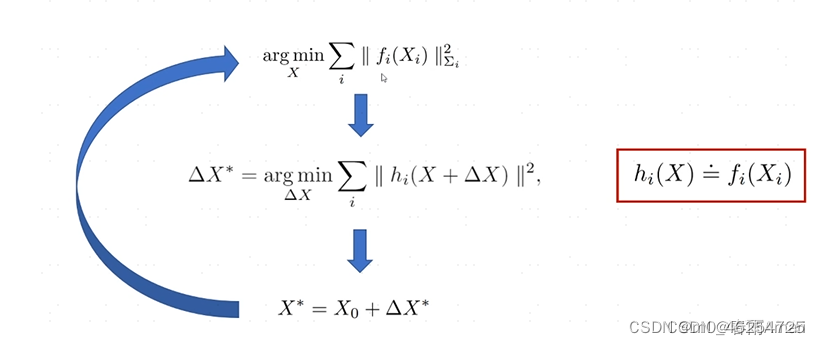
在这里插入图片描述
每一步迭代求解增量的过程，通过线性化的步骤
做一阶泰勒展开：
对于上图中的非线性最小二乘问题，对中间的式子做一阶泰勒展开，就可以将其转化为线性最小二乘问题：

现在的问题就转化成了如何求解这个线性最小二乘问题。

5、求解线性最小二乘问题

可以直接求解，也可以normal equation，常见的是normal equation
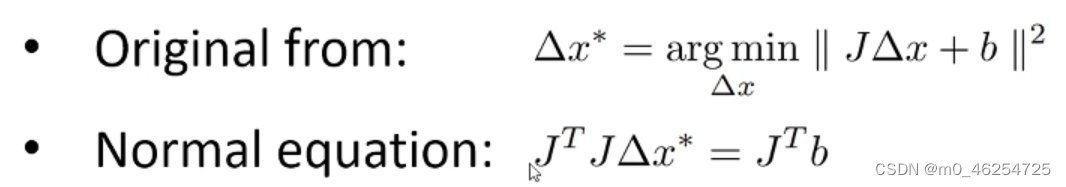
在这里插入图片描述

直接求解线性二乘法，一般通过QR分解
在这里插入图片描述
现实生活中QR分解会慢一点，所以会倾向于选择cholesky分解来做，但cholesky分解缺点是数值稳定性差一点。一般根据系统性质来选择

5、因子图求解过程

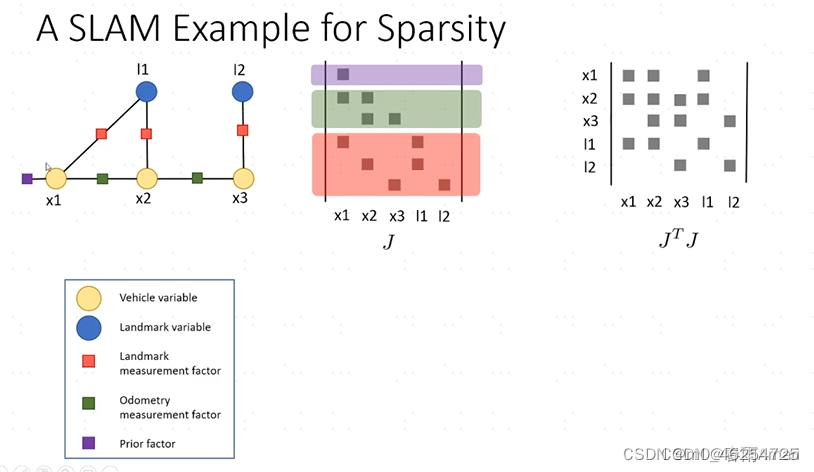
在这里插入图片描述

上图中的雅可比矩阵的每一行对应一个因子，右边的矩阵是一个信息矩阵，在现实中生成的因子图所获得的雅可比矩阵是稀疏矩阵（因为每一个观测量，相关的系统状态量很少），
这是一个很好的性质，非常有利于线性系统的求解。
一个大的SLAM矩阵稀疏性展示：
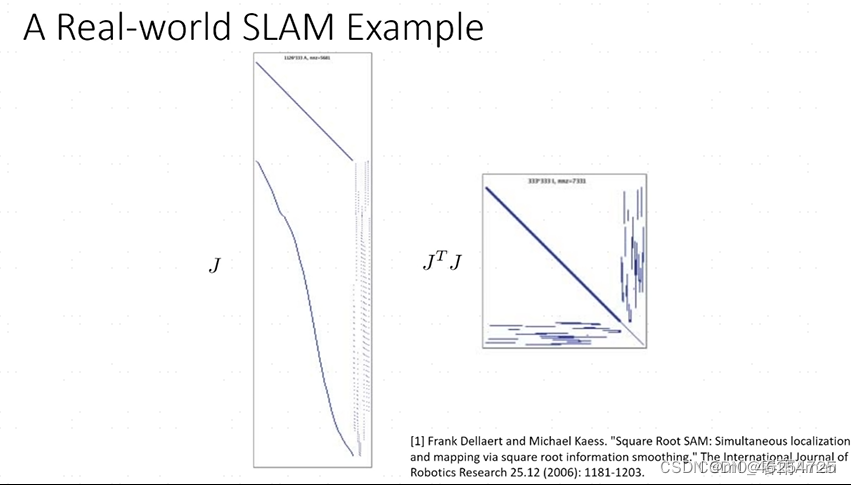
在这里插入图片描述

求解顺序

但是这个矩阵的稀疏性和变量的order有关，order不一样的话，矩阵的稀疏性体现也不一样，会出现下图所示的情况：
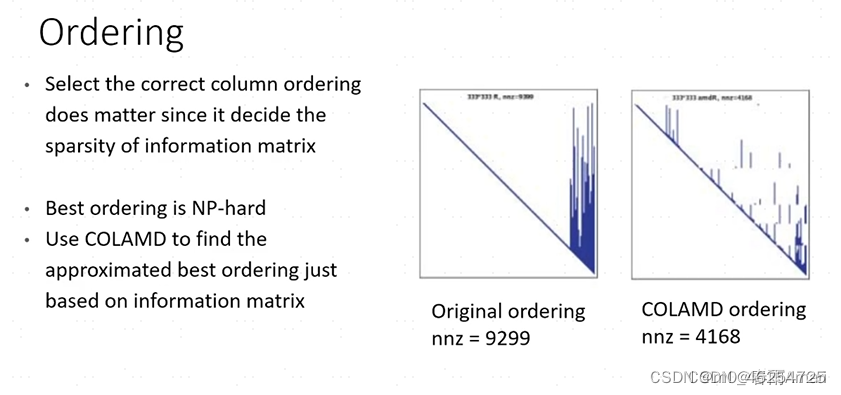
在这里插入图片描述

这种情况下不利于线性系统的求解，所以通常需要一些算法来对信息矩阵进行重排序来维持其好的稀疏性，目前较为成熟的算法为COLAMD。通过上面的描述我们知道了对于一个确定的因子图如何求解。但是常见的问题（比如SLAM问题）生成的因子图是增量的，并且在机器人运行的过程中，因子图只是又很小一部分的改变，如果我们从头对因子图进行分解来求解的话，不利于系统的实时性，那么如何解决这个问题呢？下面介绍论文isam中是怎么做的。.

5、增量推理一般分为isam1，isam2

5.1 isam增量QR分解

对给定的J进行QR分解如下：
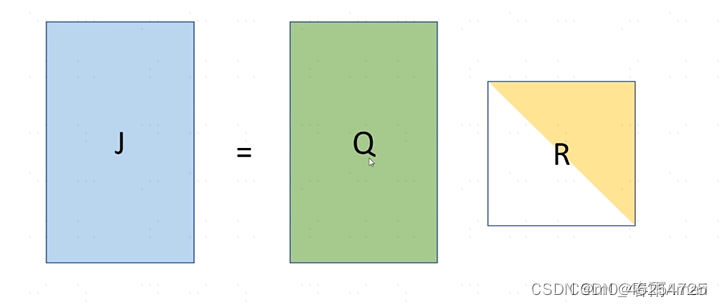
在这里插入图片描述
Q为正交矩阵，R为上三角矩阵。
想对J加入几行，一行对应一个因子。这几行的意义就是，当因子图中加入了新的节点和因子时在信息矩阵中的表现就是多了几行，问题就是怎么不在重新分解的基础上能得到新的R。
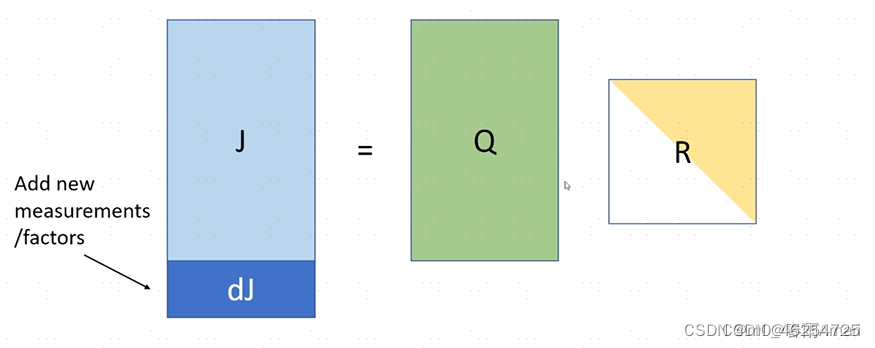
在这里插入图片描述

论文中给出的方法：
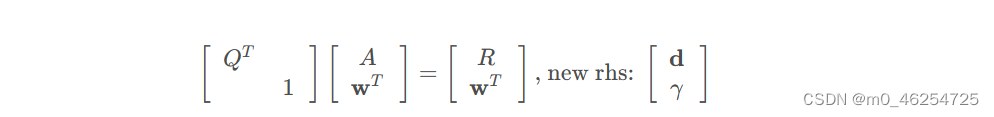
在这里插入图片描述
当获得了新的测量行时雅克比矩阵A下方多了一行新测量因子线性化项（行），该线性化项（行）列数可以比A多，用0补齐A右侧即可，且是稀疏的，因为仅有特定的参数状态（列）与该因子有关，当新的增量雅克比矩阵左乘原正交矩阵时（相差的行列用单位矩阵补齐，此时仍是正交的）就可以得到R矩阵的增量表达，增量方式与A相同，注意此时新增的行依然是稀疏的。
在R下面加了一行（非零元素）变成如下：

将增量QR分解问题，转为增量三角化R的问题，转化为如何将新的R通过正交阵变为三角阵（isam使用了Givens旋转的方法）

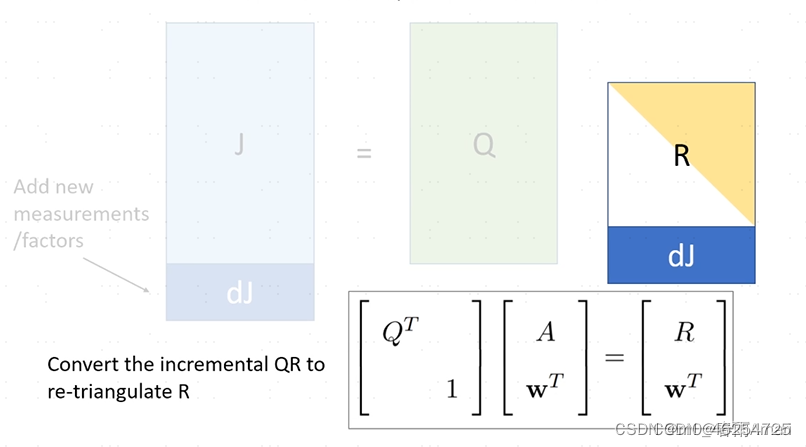
在这里插入图片描述
（A为图中的J）

5.1.1 Givens旋转

通过givens rotation可以将R变成一个新的上三角矩阵：(只需要对R矩阵进行Givens旋转变换就可以将下面的非零项消除，得到新的R矩阵:)
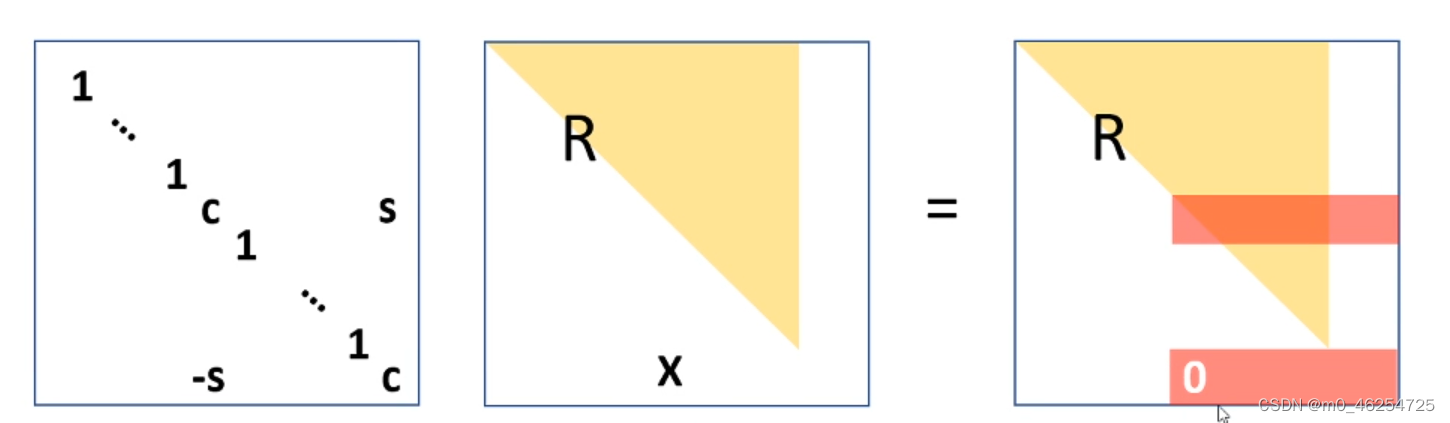
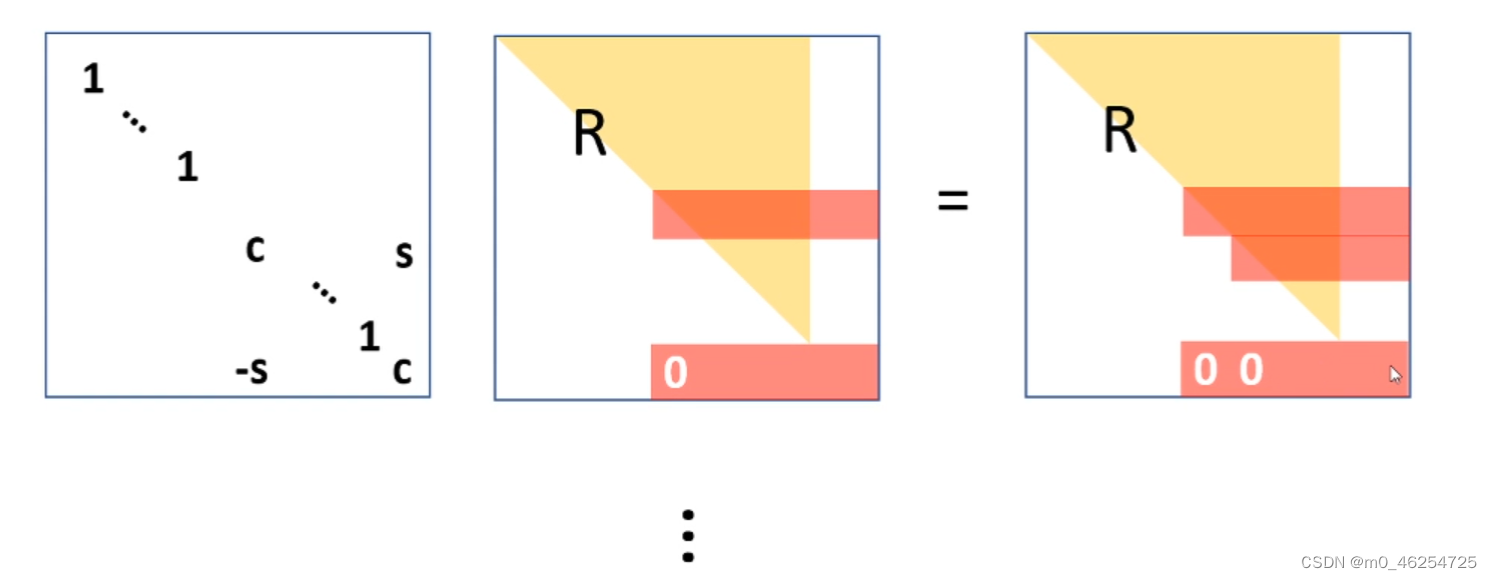
在这里插入图片描述

但得到了密集的三角矩阵。

这样就完成了一次增量更新，我们注意到使用iSAM在这种情况下可以只对新增的测量因子线性化，也不需要对雅可比矩阵A重新QR分解，就得到了我们想要的结果，这一过程像滤波算法一样简单，但却可以得到批量优化一样好的全局最优效果。这就是iSAM的闪光点。

6、isam缺点

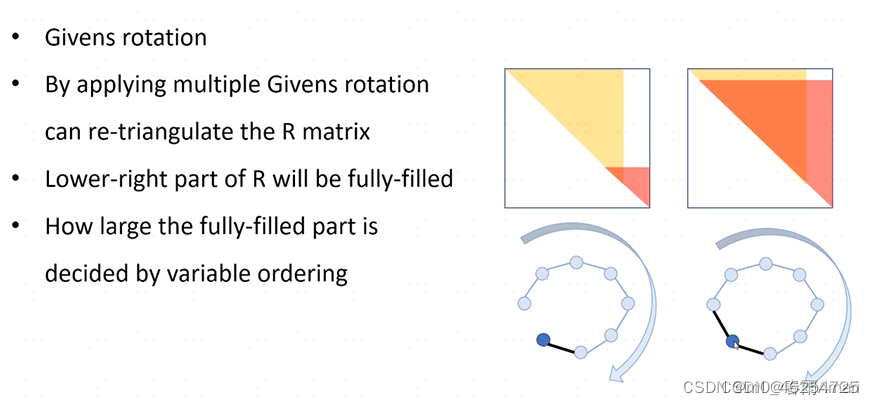
得到如此好的结果是基于R矩阵是稀疏的前提条件。Givens旋转是在n维空间中旋定两组正交基张成的空间中旋转。
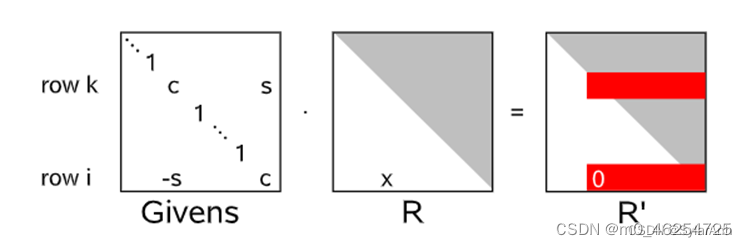
在这里插入图片描述
也就是说在消去R底部对应行的过程中，上面的某一行也在发生着改变，稀疏性会逐渐的遭到破坏如下图所示

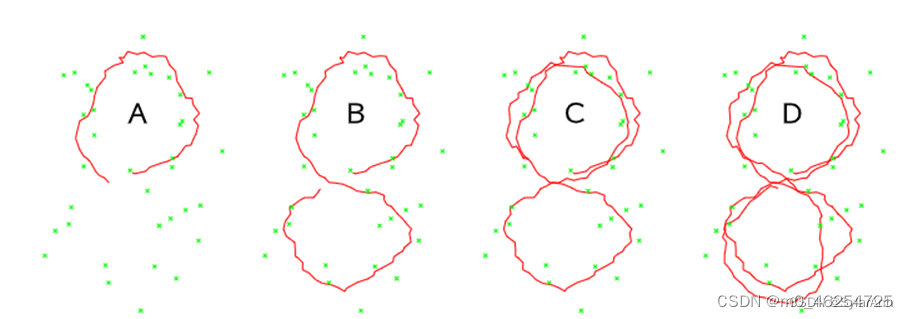
但是随着因子的增加，也会带来一个问题，就是如果我新加的因子只影响上一时刻的因子的时候，这个矩阵依然是有很好的稀疏性，但是如果新加入的因子是回环，那么givens rotation将影响之前的所有节点，使R矩阵变得稠密（许多非零元素），如下图所
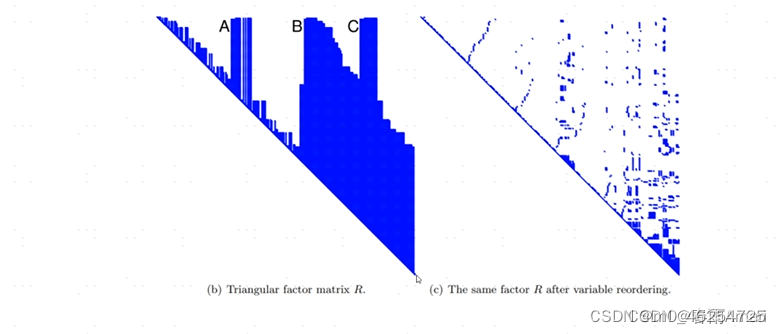
在这里插入图片描述
现实中做一个增量位姿图优化，得到的R矩阵如下面的左图所示，导致三角阵越来越大，右图是重排序后的R

这时候就体现出了isam1的问题，在经过以一定的时间后就需要对元素进行重新排序，将稠密矩阵变得稀疏，恢复1矩阵的稀疏性：
在这里插入图片描述

isam1讨论的所有增量QR分解都是求解线性系统的方法。
增量求解因子图实际上用的是迭代法，迭代中的每一步用线性的方法。实际上做的是增量每一步线性化，在每一步求解。但在做线性增量QR分解时，线性化点一直没有变。
除了重排序，线性化点还需要定期做线性化

因此iSAM抛出问题：
如何减少重排序的次数，如何降低新增状态量，对R矩阵稀疏性的破坏程度。
如何解决定期做线性化

参考：
https://blog.csdn.net/weixin_45112559/article/details/126146289？ydreferer=aHR0cHM6Ly9jbi5iaW5nLmNvbS8%3D
https://blog.csdn.net/qq_35158703/article/details/126953856
论文名：iSAM: Incremental Smoothing and Mapping
作者Michael Kaess, Student Member, IEEE, Ananth Ranganathan, Student Member, IEEE,and Frank Dellaert, Member, IEEE，2008