数二高数笔记

1、大纲

2.常用的等价无穷小

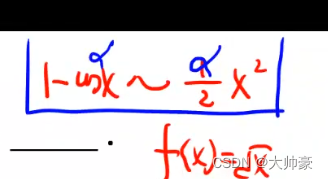
3、常用结论

4、利用等价无穷小替换极限

5、利用有理运算法则求极限

6、型常用理论

7、泰勒公式求极限

8、讨论间断点例题

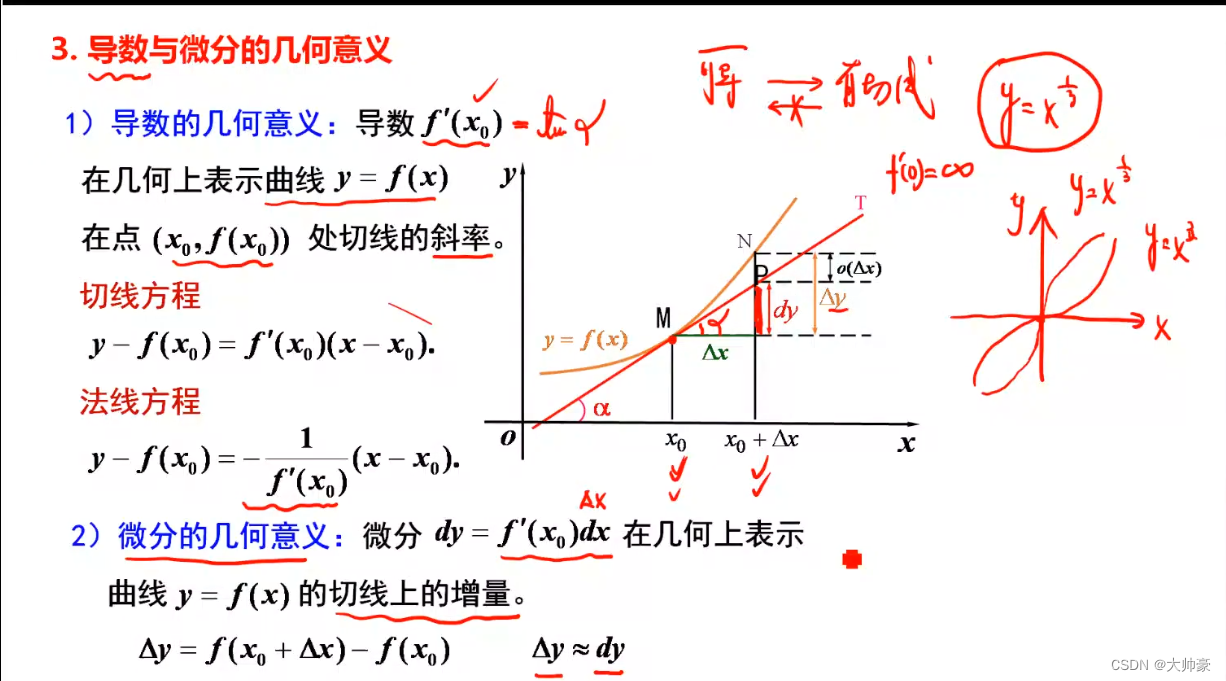
9、导数与微分的几何意义

10、导数公式及求导法则

11、高阶导数

12、斜渐近线、曲率、曲率半径

13、求斜渐近线的另一种方式

14、零点定理、罗尔定理例题

15、原函数存在定理

16、不定积分基本公式

17、部分积分法

18、三种积不出的函数

19、三角有理式积分

20、简单无理函数积分

21、求原函数举例

22、定积分性质

23、积分上限的函数

24、求定积分举例

25、变上限积分例题

26、收敛//发散    比较法

27、积分在几何上的运用

28、切线方程的写法、形心

 29、线性微分方程的解的结构

30、一阶微分方程

31、可降阶的微分方程

32、多元函数的连续性

33、高阶偏导数

34、全微分

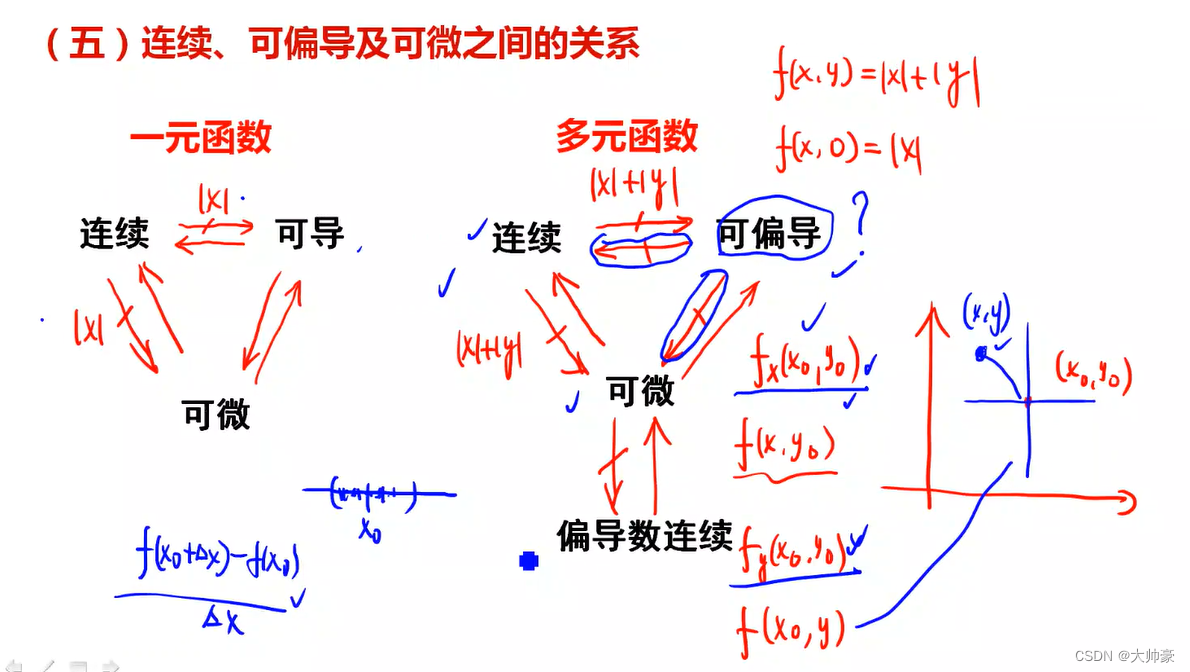
34、连续、可偏导、可微联系

35、复合函数、隐函数微分法

36、求极值

37、二重积分

38、原函数与导数的奇偶性、周期性关系

39、有界性

40、分左右极限求极限

41、局部保号性、有界性

42、无穷小的性质、无穷大

43、基本极限求极限

44、无穷 - 无穷类型求极限

45、无穷 / 无穷类型求极限

46、0 / 0类型求极限

47、1 无穷次方型求极限

48、0*无穷型求极限

49、其他类型求极限

50、n项和的数列求极限

51、何时用夹逼、何时用定积分

52、n项连乘的数列求极限

53、递推求极限

54、判断原函数在某点是否可导的充要条件

55、f(x) 与 |f(x)| 的可导、连续关系

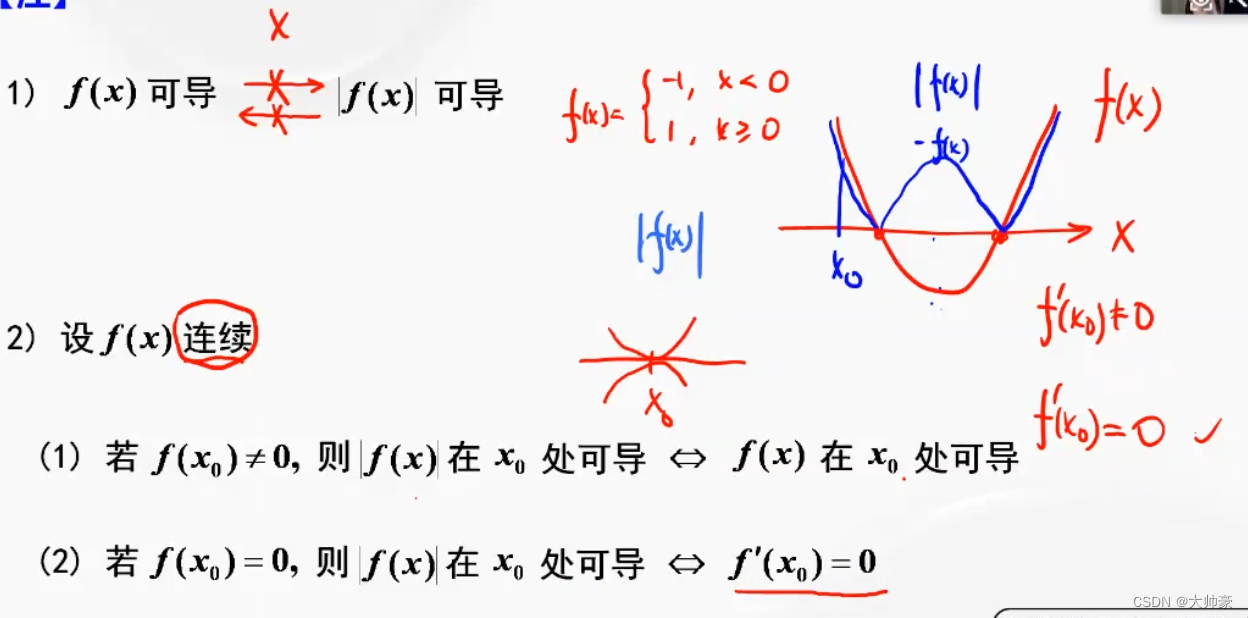
56、极值的充分条件

57、方程根的存在性及其个数    证明方法

58、微分中值定理有关证明题

59、构造辅助函数

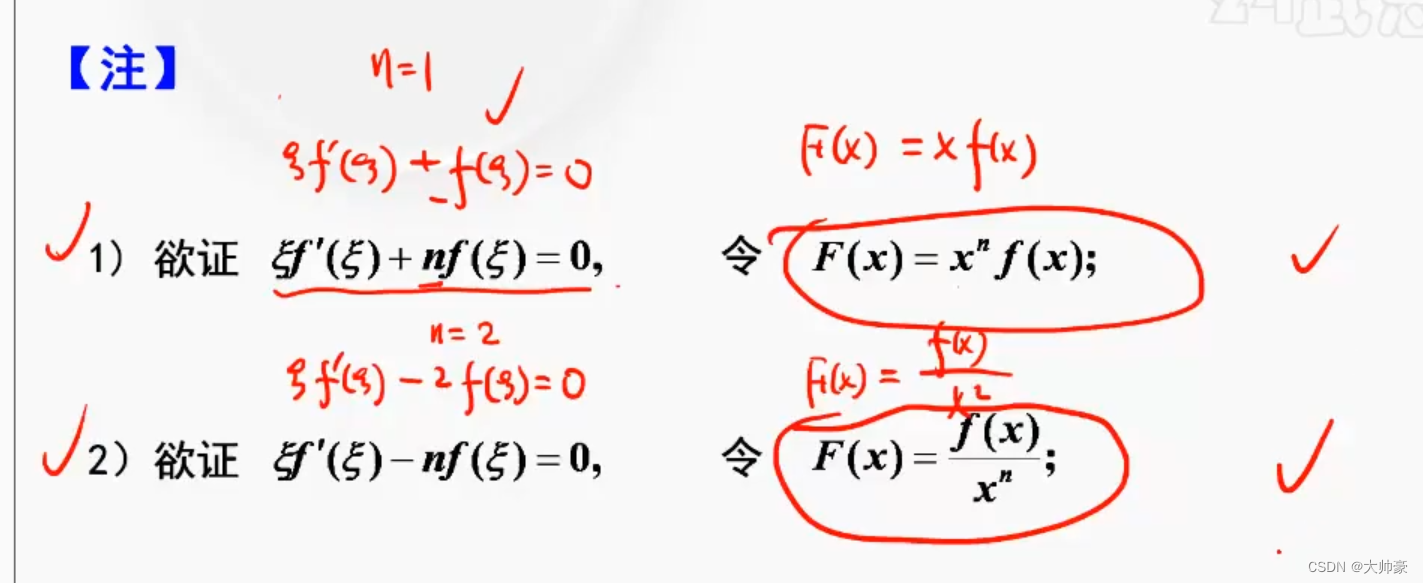
60、证明存在两点

61、证明存在一个中值点

62、三种主要的积分法

63、定积分的存在性质

64、变上限积分函数及应用

65、F(x) -- f(x) -- f(x)导数关系

66、多元函数求极值

67、多元函数连续性质

68、全微分

错题

1、定积分的变量代换

2、不定积分的公式

3、全微分的定义题

4、保号性

5、单调有界

6、f(x)连续，导数大与0相关结论

7、不等式证收敛

8、变限积分求极限

9、数列求极限用到洛必达时需转换成函数求极限

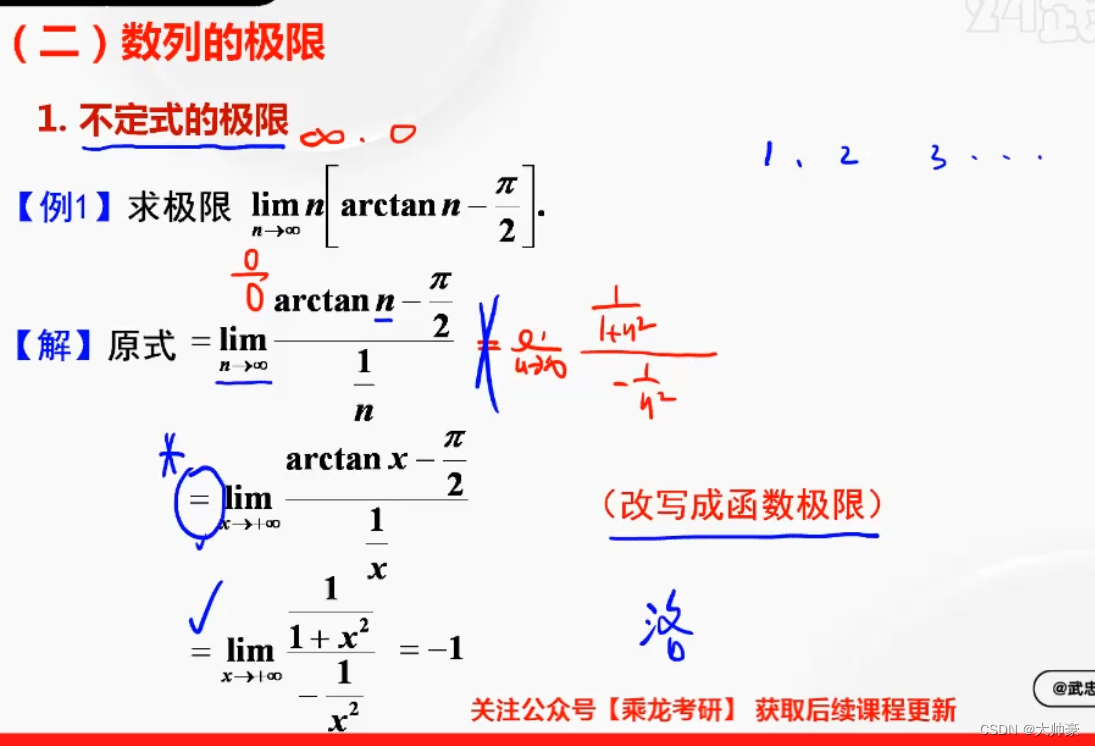
10、判断变限积分大小相关结论

11、导数定义求极限

12、导数的可积、连续与其原函数的关系

13、定积分的计算

14、区间不变

15、变上限积分证明题

16、通过极限求原函数（导数定义）

17、微分方程证明题