通信原理04：数字信号基带传输

m0_46521579

已于 2022-09-20 20:22:22 修改

阅读量3.4k

点赞数 4

分类专栏：通信原理文章标签：学习

于 2022-09-19 00:20:46 首次发布

本文链接：https://blog.csdn.net/m0_46521579/article/details/126924401

版权

通信原理专栏收录该内容

9 篇文章

订阅专栏

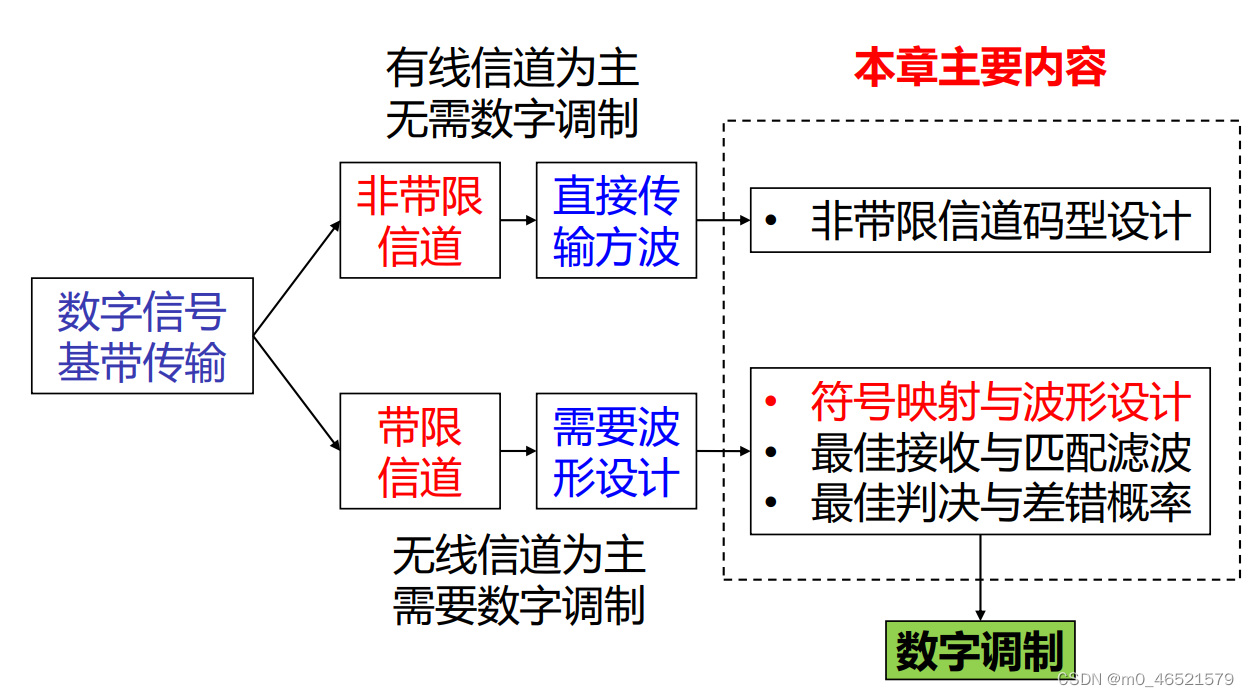
一、线路码型

1. 码型设计基本原则

码型设计是数字信息的电脉冲表示，使数字信息变换为适合于给定信道传输特性的频谱结构。

码型设计的基本原则：

（1）对于传输频带低端受限的信道，一般来讲线路传输码型的频谱中应不含直流分量；

（2）码型变换（或码型编译码）过程应对任何信源具有透明性，即与信源的统计特性无关；

（3）便于从基带信号中提取位定时信息；

（4）便于实时监测传输系统信号传输质量，即能检测出基带信号码流中错误的信号状态；

（5）误码增值愈少愈好（无误码扩散）；

（6）当采用分组形式的传递码型时（如5B6B、4B3T 码等），在接收端不但要从基带信号中提取位定时信息，而且要恢复出分组同步信息，以便将收到的信号正确地划分成固定长度的码组（帧同步/分组同步）；

（7）尽量减少基带信号频谱中的高频分量；

（8）编译码设备应尽量简单。

2. 二元码

$a = \frac{T}{2}$ ，主瓣： $|f| \leq \frac{1}{2a} = \frac{1}{T}$

mBnB码：将m bit的信息用n个二元码表示

编码效率： $\eta = \frac{m \log_{2} 2 }{n \log_{2} 2} = \frac{m}{n}$

数字双相码：1B2B码， $\eta = 50%$

3. 三元码

在三元码数字基带信号中，信号幅度的取值有三个：+1、0、-1

（1）传号交替反转码（AMI）

非零正负交替，无直流分量，不易提取定时信息

（2）HDB3

1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0

1 0 0 0 V 0 1 1 B 0 0 V B 0 0 V 1 0 0 0 V 1 0 0

+1 0 0 0 V 0 -1 +1 -1 0 0 V +1 0 0 V -1 0 0 0 V +1 0 0

+1 0 0 0 +1 0 -1 +1 -1 0 0 -1 +1 0 0 +1 -1 0 0 0 -1 +1 0 0

mBnT码：将m bit的信息用n个三元码表示

编码效率： $\eta = \frac{m \log_{2} 2}{n \log_2 3}$

HDB3：1B1T码

4. 多元码

二、符号映射与波形成形

1. 比特、符号和波形

比特：信息单位， $\{0,1\}$

符号：物理概念，离散时间，离散幅度。比特在现实世界中传输需要映射为物理量，如电压 $\{+A,-A\}$ 。给定一个符号集合 $\{ a_1,a_2,a_3,\dots,a_M \}$ ，其可以承载的比特数量为 $n = \log_2 M$ 。传输一个符号所需的时间为 $T_s$ ，则符号速率为 $R_s = \frac{1}{T_s}$ ，比特速率为 $R_b = R_s \log_2 M$ 。

波形：将离散的符号映射为时间和幅度均连续的模拟信号。

$g(t)$ 是成形脉冲，是将离散的符号映射为通信波形的纽带。无线通信要求传输信号的频域带宽有限，因此要求 $g(t)$ 为带限信号。

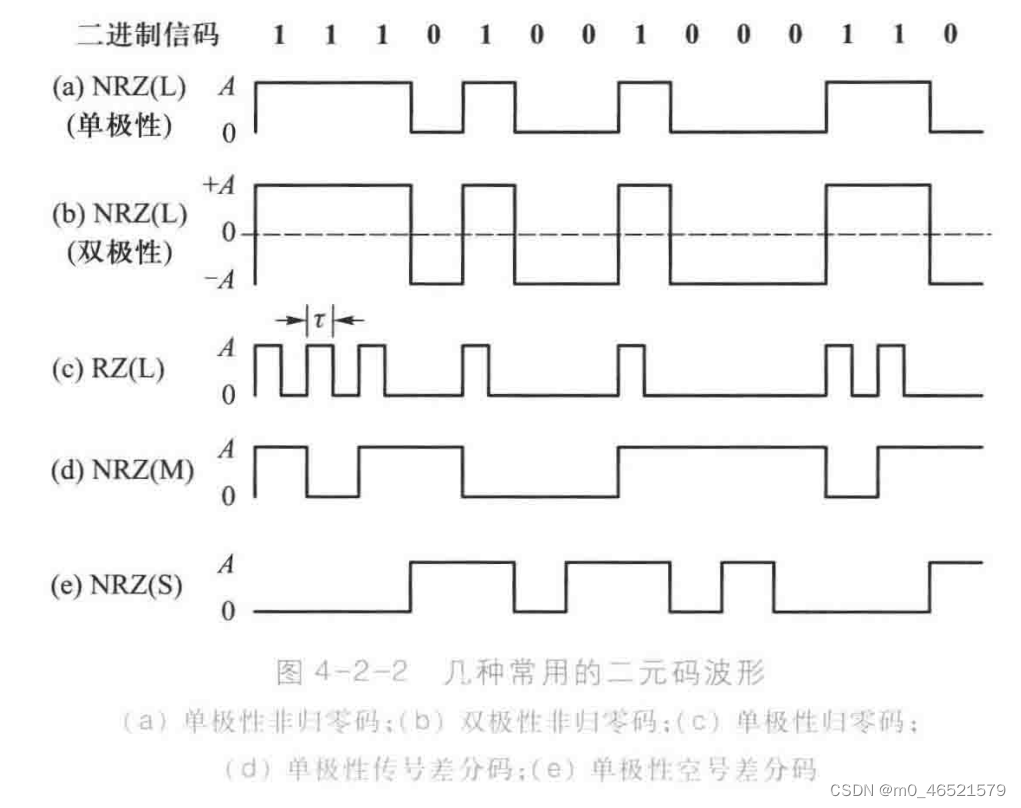
2. 奈奎斯特第一准则（采样点无失真准则）

采样点无失真： $a(nT_s) = a_n$

对于 $t = nT_s$ ，

$a(t) \cdot \sum_{n=-\infty}^{\infty} \delta(t-nT_s) = \sum_{n=-\infty}^{\infty} a(nT_s) \delta(t-nT_s)$

整理得

$\sum_{k=-\infty}^{\infty} a_k g(t-kT_s) \cdot \sum_{n=-\infty}^{\infty} \delta(t-nT_s) = \sum_{n=-\infty}^{\infty} a_n \delta(t-nT_s)$

$g(t) \otimes \sum_{k=-\infty}^{\infty} a_k \delta(t-kT_s) \cdot \sum_{n=-\infty}^{\infty} \delta(t-nT_s) = \sum_{n=-\infty}^{\infty} a_n \delta(t-nT_s)$

$F\left[ \sum_{n=-\infty}^{\infty} a_n \delta(t-nT_s) \right ] = \int_{-\infty}^{\infty} e^{-jwt}\left( \sum_{n=-\infty}^{\infty} a_n \delta(t-nT_s) \right ) dt \\= \int_{-\infty}^{\infty} \sum_{n=-\infty}^{\infty} a_n e^{-jwnT_s}\delta(t-nT_s) dt \\= \sum_{n=-\infty}^{\infty} a_n e^{-jwnT_s} \int_{-\infty}^{\infty} \delta(t-nT_s) dt\\=\sum_{n=-\infty}^{\infty} a_n e^{-jwnT_s}$

$G(w) \sum_{k=-\infty}^{\infty} a_k e^{-jwkT_s} \otimes \frac{1}{2\pi} \frac{2\pi}{T_s} \sum_{n=-\infty}^{\infty} \delta(w-nw_s) = \sum_{n=-\infty}^{\infty} a_n e^{-jwnT_s}$

$G(w) \otimes \frac{1}{T_s} \sum_{n=-\infty}^{\infty} \delta(w-nw_s) = 1$

$\sum_{n=-\infty}^{\infty} G(w-nw_s) = T_s$

将波形传递函数频域响应𝐺(𝜔)实部和虚部均以2𝜋/𝑇𝑠为单位进行分段；
将各分段都沿着𝜔轴平移到[− 𝜋/𝑇𝑠 , 𝜋/𝑇𝑠 ]之间，并将它们叠加起来；
实部叠加结果为固定值（常数），虚部叠加结果为0。

3. 符号速率与频谱效率

符号速率 $R_s$ ：单位时间内传输的符号数量，signal/s = Baud

比特速率 $R_b$ ：单位时间内传输的比特数量，bit/s

$R_b = R_s \log_2 M$

频谱效率： $\eta = \frac{R_b}{ W }$ ，单位频谱上所承载的通信速率

由奈奎斯特第一准则可知： $2W \geq R_s$ ，W单位为Hz

$\eta = \frac{R_s \log_2 M}{ W } \leq \frac{2W \log_2 M}{W} = 2\log_2 M$

4. 升余弦成形滤波器

下降沿起始于 $\frac{R_s}{2}(1-\alpha) = \frac{(1-\alpha)}{2T_s}$ ，终止于 $\frac{R_s}{2}(1+\alpha) = \frac{(1+\alpha)}{2T_s}$

整个下降沿关于 $f=\frac{R_s}{2}, H = \frac{T_s}{2}$ 中心对称。

带宽： $W = \frac{R_s}{2} (1+\alpha)$

频谱效率： $\eta = \frac{R_s}{W} = \frac{2}{1+\alpha}$

5. 通信波形的功率谱

$a(t) = \sum_{k=-\infty}^{+\infty} a_k \cdot g(t-kT_s)$

推导过程略

$P_a(f) = \frac{\sigma_a^2}{T_s} |G(f)|^2 + \frac{m_a^2}{T_s^2} \sum_{k=-\infty}^{+\infty} \left|G\left( \frac{n}{T_s} \right) \right|^2 \delta(f-nT_s)$

其中， $m_a$ 为符号均值， $\sigma_a^2$ 为符号方差。

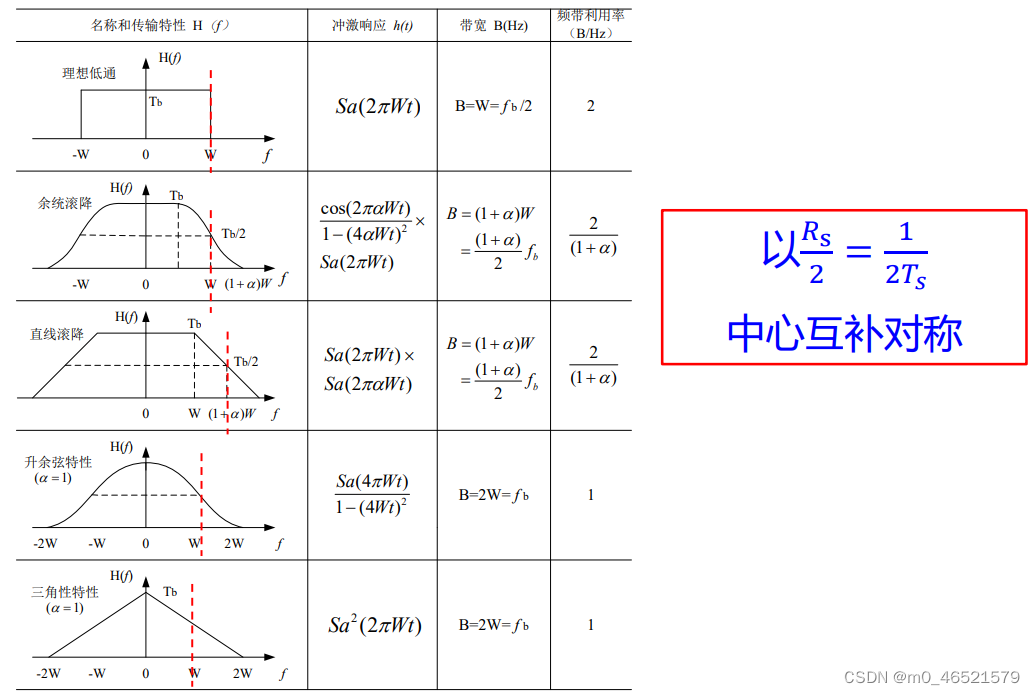
三、最佳接收与匹配滤波

实际信道存在噪声，因此接收机前端一般存在滤波器滤去噪声。

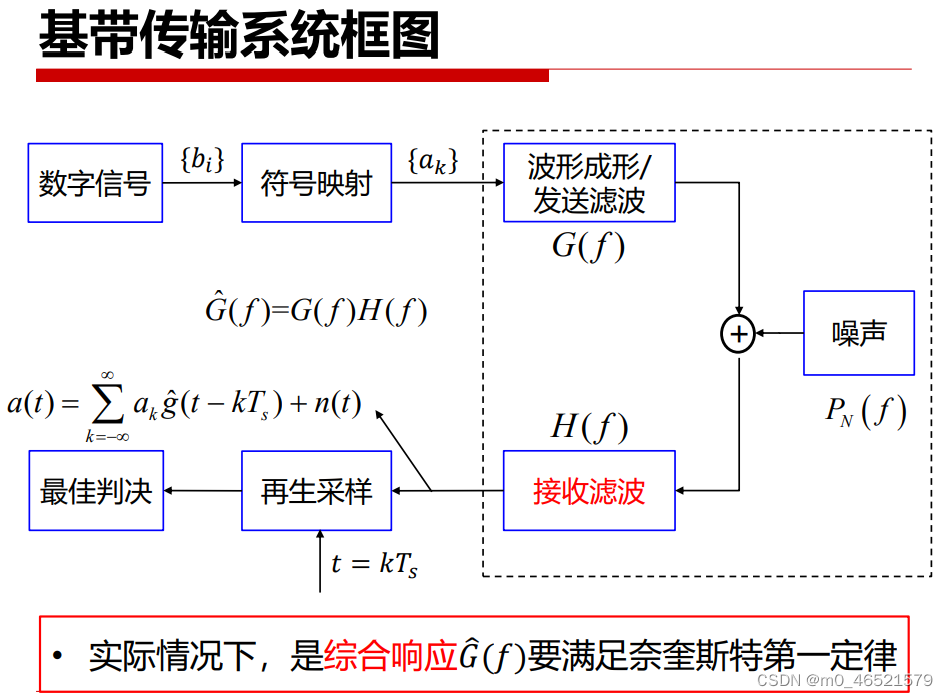
1. 信噪比最大化

$Y(t) = a \cdot g(t) +N(t)$

$\hat{a} = \int_{-\infty}^{+\infty} Y(t)h(t) dt = a\int_{-\infty}^{\infty} g(t)h(t) dt + \int_{-\infty}^{\infty} N(t) h(t) dt$

$N = E\left[ \left( \int_{-\infty}^{\infty} N(t) h(t) dt \right )^2 \right ] \\= E\left[ \int_{-\infty}^{\infty} N(t) h(t) dt \int_{-\infty}^{\infty} N(\tau) h(\tau) d\tau \right ] \\= E\left[ \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} N(t) h(t)N(\tau) h(\tau) d\tau dt \right ] \\= E\left[ \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} N(t) h(t)N(\tau) h(\tau) d\tau dt \right ] \\= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} E\left[ N(t)N(\tau) \right ] h(t)h(\tau) d\tau dt \\= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \frac{n_0}{2}\delta(t-\tau) h(t)h(\tau) d\tau dt \\= \frac{n_0}{2} \int_{-\infty}^{\infty} h(t) \left( \int_{-\infty}^{\infty} \delta(t-\tau) h(\tau) d\tau \right ) dt \\= \frac{n_0}{2} \int_{-\infty}^{\infty} h(t) \cdot (h(t) \otimes \delta(t) )dt \\= \frac{n_0}{2} \int_{-\infty}^{\infty} h^2(t) dt$
$S = \left[ a\int_{-\infty}^{\infty} g(t)h(t) dt \right ]^2 = a^2 \left[ \int_{-\infty}^{\infty} g(t)h(t) dt \right ]^2 \\ \leq a^2 \int_{-\infty}^{\infty} g^2(t) dt \int_{-\infty}^{\infty} h^2(t) dt$

当且仅当 $h(t) = g(t)$ 时等号成立

$SNR = \frac{S}{N} = \frac{a^2 \left[ \int_{-\infty}^{\infty} g(t)h(t) dt \right ]^2}{\frac{n_0}{2} \int_{-\infty}^{\infty} h^2(t) dt} \leq \frac{a^2 \int_{-\infty}^{\infty} g^2(t) dt \int_{-\infty}^{\infty} h^2(t) dt }{\frac{n_0}{2} \int_{-\infty}^{\infty} h^2(t) dt} = \frac{a^2}{n_0 /2} \int_{-\infty}^{\infty} g^2(t) dt$

当且仅当 $h(t) = g(t)$ 时等号成立。

即，当 $h(t) = g(t)$ 时，再生判决输出信噪比最大。

$\hat{a} = \int_{-\infty}^{\infty} Y(t) g(t) dt$

$\hat{a} = \int_{-\infty}^{\infty} Y(t) h_m(t_0 -t) dt$

令 $g(t) = h_m(t_0 - t)$ ，等价于 $h_m(t) = g(t_0 - t)$

2. 匹配滤波器的信噪比增益

匹配滤波器输入信噪比：

$S_{\rm in} = E_s R_s = R_s a^2 \int_{-\infty}^{\infty} g^2(t) dt$

$N_{\rm in} = \frac{n_0}{2} \cdot 2W = n_0 W$
$SNR_{\rm in} = \frac{S_{\rm in}}{N_{\rm in}} = \frac{R_s a^2 }{n_0 W} \int_{-\infty}^{\infty} g^2(t) dt$

匹配滤波器输出信噪比：

$SNR_{\rm out} = \frac{a^2}{n_0 /2} \int_{-\infty}^{\infty} g^2(t) dt$

匹配滤波器信噪比增益：

$G = \frac{SNR_{\rm out}}{SNR_{\rm in}} = \frac{\frac{a^2}{n_0 /2} \int_{-\infty}^{\infty} g^2(t) dt}{ \frac{R_s a^2 }{n_0 W} \int_{-\infty}^{\infty} g^2(t) dt } = \frac{2W}{R_s} = \frac{2}{\eta}$

匹配滤波的输出信噪比与频谱效率或滚降系数均无关。

3. 根升余弦波形成形函数

4. 等效基带模型

四、最佳判决与差错概率

1. 最佳判决的若干准则

2. M元ASK星座

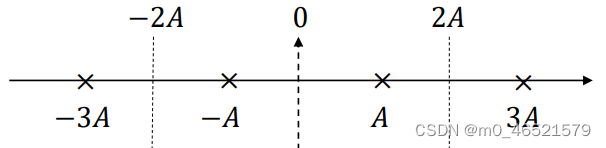
$E_s = \frac{2\sum_{k=0}^{\frac{M-2}{2}}(2k+1)^2A^2}{M} \\= \frac{2A^2}{M} \sum_{k=0}^{\frac{M}{2} -1} (2k+1)^2 \\= \frac{2A^2}{M} \left[ 4\frac{(\frac{M}{2}-1) \frac{M}{2} (M-2+1)}{6} +4 \frac{\frac{M}{2}(\frac{M}{2} -1)}{2} + \frac{M}{2} \right ] \\= A^2 \left[ 2 \frac{(\frac{M}{2}-1) (M-2+1)}{3} + 2(\frac{M}{2} -1) + 1 \right ] \\= \frac{M^2-1}{3} A^2$

$A = \sqrt{\frac{3E_s}{M^2-1}}$

3. 数字基带传输的差错分析方法

双极性ASK星座点：

$A =\{ -(M-1)A,\dots,-3A,-A,A,3A,\dots,(M-1)A \}$

判决门限：

$-(M-2)A,\dots,-2A,0,2A,\dots,(M-2)A$

以星座点 $-(M-1)A$ 为例，当 $n>A$ 时，产生误判，则条件差错的概率为

$\int_{A}^{+\infty} \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{x^2}{2\sigma^2}} dx |_{\sigma^2 = \frac{n_0}{2}} \\= \int_{A}^{+\infty} \frac{1}{\sqrt{n_0\pi}} e^{-\frac{x^2}{n_0}} dx \\= \int_{\frac{A}{\sqrt{n_0/2}}}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{z^2}{2}} dz\\= Q\left( \frac{A}{\sqrt{n_0/2}} \right )$

以星座点 $A$ 为例，当 $|n|>A$ 时，会产生误判，则条件差错的概率为
$\int_{-\infty}^{-A} + \int_{A}^{+\infty} \frac{1}{\sqrt{n_0\pi}} e^{-\frac{x^2}{n_0}} dx \\= 2 \int_{\frac{A}{\sqrt{n_0/2}}}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{z^2}{2}} dz\\= 2 Q\left( \frac{A}{\sqrt{n_0/2}} \right )$

无符号率：

$p_s = \frac{1}{M} \left[ (M-2) 2 Q\left( \frac{A}{\sqrt{n_0/2}} \right ) + 2 Q\left( \frac{A}{\sqrt{n_0/2}} \right ) \right ] = \frac{2(M-1)}{M} Q\left( \frac{A}{\sqrt{n_0/2}} \right )$

有之前计算可知： $E_s = \frac{M^2 -1}{3}A^2$

整理可得：

$p_s = \frac{2(M-1)}{M} Q\left( \sqrt{\frac{3E_s}{M^2 -1}} \frac{1}{\sqrt{n_0/2}} \right ) = \frac{2(M-1)}{M} Q\left( \sqrt{\frac{6}{M^2 -1} \frac{E_s}{n_0}} \right )$