SPSS相关性分析

一、pearson

适应于：

* 适用于定距、定比类型的变量。检测用t统计量：其中统计量t服从自由度（n-2）的分布【变量就是n，加入有10个变量，自由度就是10-2=8】

* 变量必须是成对的数据

* 两个变量为线性关系

* 变量属于正态分布

1 .温度与湿度正相关

先在变量视图表格里面输入数据

在输入数据视图表格

两个表格输入结束后，点击 分析–>相关–>双变量

选项——选择平均值和标准差、叉积偏差和协方差（为了后面表格更丰富而已）——继续

皮尔逊——双尾检验——确定

分析结果如图，温度与湿度相关系数为0.961，说明存在显著的正向线性相关性。

2、销售额和价格负相关

例题：探究某种商品的销售额是否与价格有关

销售额	价格
2.00	46.00
3.00	42.00
4.00	41.00

清除掉数据视图就可以，然后加入新的数据

分析——相关——双变量——把销售额和价格放在右边的变量框里

选项——选择平均值和标准差、叉积偏差和协方差（为了后面表格更丰富而已）——继续

皮尔逊——双尾检验——确定

由图可知，皮尔逊为-0.930，属于高度负相关

通过双尾检验，如果大于0.05，表示存在偶然性误差，不通过检验

二、卡方检验

适应于：定类与定类；定类与定序

1、性别与吸烟的关系类型1

1.2分别代表男生和女生，1.0代表吸烟与不吸烟

性别	吸烟
1	1
1	1
2	0
2	0

输入数据视图

输入变量视图

找到 分析——描述统计——交叉表

把性别和吸烟分别放在行与列中，然后选择卡方，选择Phi和克莱姆V（这里可以任意选择，无非就是多了几组数据集），选择继续，选择确定

显著性检验是0.079，大于0.05，所以吸烟与性别不存在关系。（小于0.05，表示有关系；大于0.05表示没有关系)

2、性别与吸烟的关系类型2

与第一个不同的是，第二种用频数来区分

	吸烟（人数）	不吸烟（人数）
男性	15	5
女性	3	17

输入数据视图

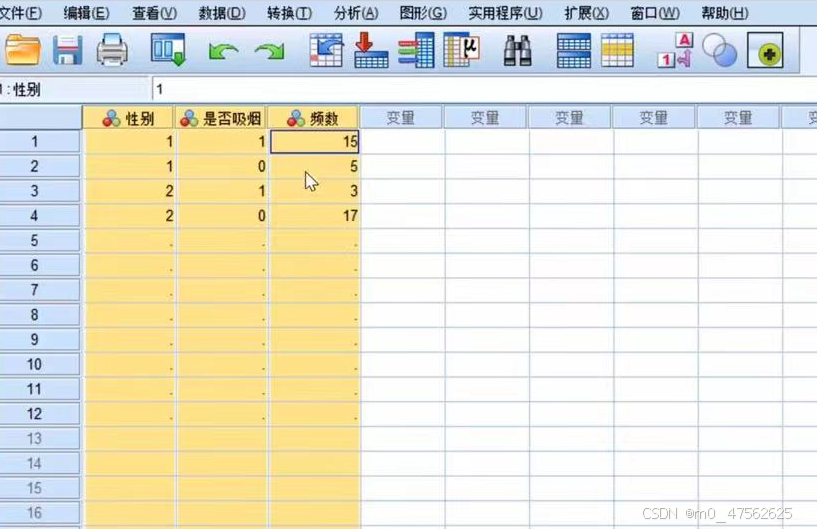
数据——个案加权

选中个案加权系数，把频数拉过来，点击确定

后面在做分析——描述统计——交叉表等步骤，与上面的步骤一样。可以看到显著性检验的数值为0.000，所以吸烟与性别高度相关。

三、Eta系数检测

适用于

定类与定距，定类与定序

1、例题1：探究某种药物用量程度是否与疼痛感有关

服用药物5毫克用1表示，10毫克用2表示

（疼痛感定距变量，药量只有两种为定类变量，也可以为定序变量）

药量	疼痛感
1	9
1	5
2	15
2	22

先输入变量视图数据，在输入数据视图数据

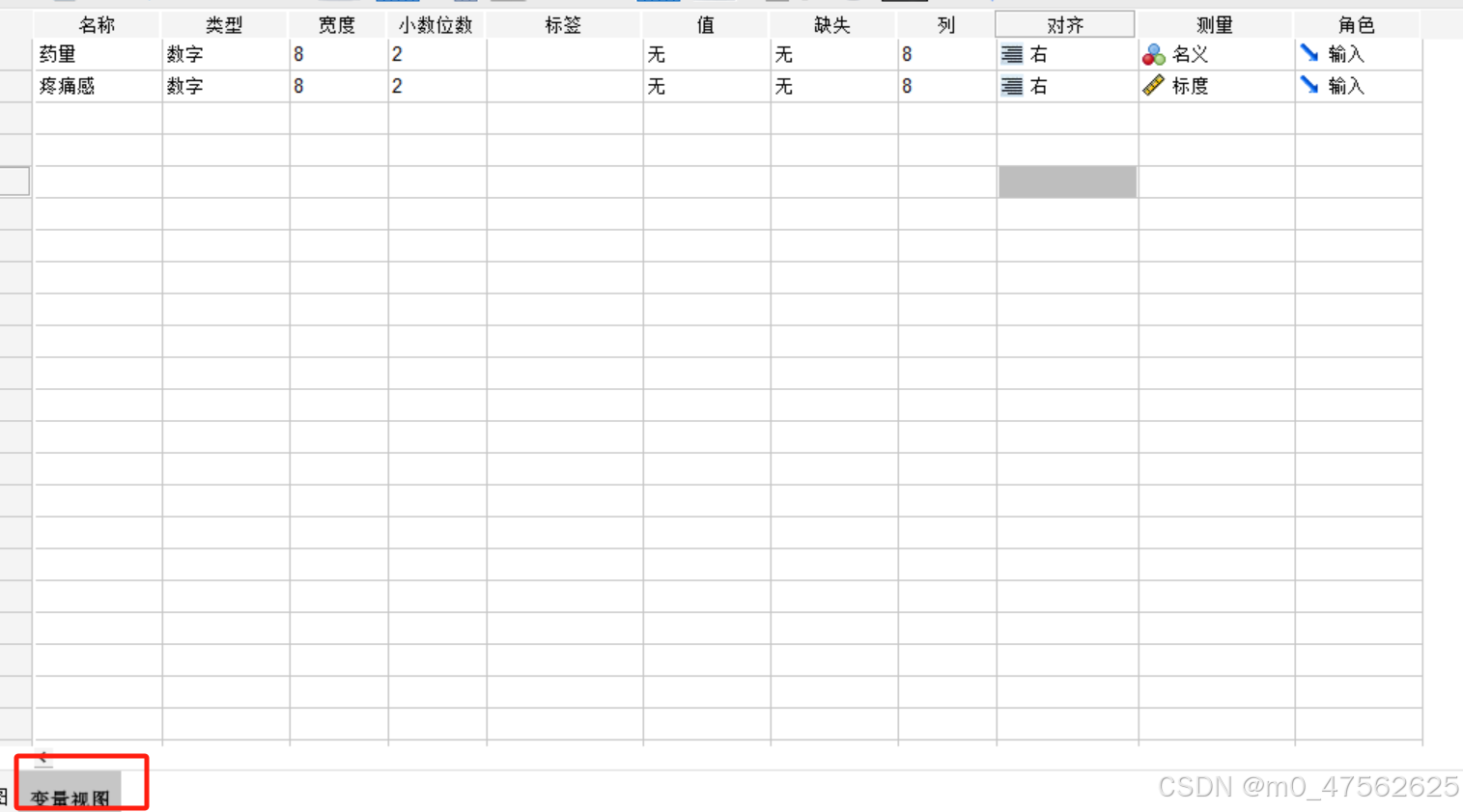
分析——描述统计——交叉表

一般行表示因变量，列表示自变量，所以把疼痛感放进行，药量放进列

统计——相关性——继续——确定

phi大于0.5，就是相关。phi为0.910，所以为高度相关

同时，皮尔逊R为0.675，phi大于皮尔逊意味着不是严格的线性关系，而是非线性关系

四、Spearman与Kendall检验

适用于

定序与定序

定序与定距

1、例题1：用的销售额与价格的数据进行的Spearman分析

输入数据视图、变量视图的数据

分析——相关——双变量——选择斯皮尔曼

数据可得到，负相关

2、销售额与价格的Kendall分析

其他步骤都一样

分析——相关——双变量——勾选Kendall

五、偏相关分析

控制变量，研究其他两个变量的关系

 1、土壤侵蚀量、降雨强度、降雨量

两个数据表

分析——相关——偏相关

土壤侵蚀量、降雨量 放在变量——降雨强度 放在控制

选项——选中平均值和标准差、零阶相关性——继续

双尾——确定

在控制变量的情况下，土壤侵蚀量与降雨量的关系更密切了