【SVM】简单介绍（一）

1、结构风险最小化

我们想要在未知的数据上得到低的错误率，这叫做structural risk minimization;相对的，训练误差叫做empirical risk minimization

要是我们能有这样一个式子就好了：
$$\text{ Test error rate }<=\text{ train error rate }+f(N,h,p)$$
其中，
$\mathrm{N}=$ size of training set,
$\mathrm{h}=$ measure of the model complexity,
$p=$ the probability that this bound fails

我们需要一个$p$来限制最差的测试集的情况。然后我们就能通过选择模型复杂度$h$来最小化测试误差率的上界。

2、VC维（Vapnik-Chervonenkis dimension）

VC维就是衡量模型复杂度的一个重要概念

选择$n$个样本点，我们随机的给它们分配标签，如果我们的模型都能将它们分开，则样本的VC维$>=n$,我们不断地增大$n$，直到模型不能分开为止。模型能分开的最大的$n$值就是模型的VC维。

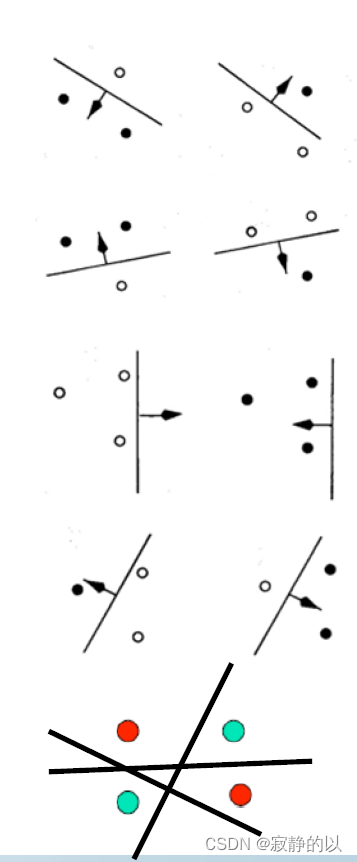
考虑一条二维空间的一条直线的复杂度。如上图所示，对于三个数据点，无论我们如何分配标签，直线都能很好的将样本正确分类。但是对于四个数据点，直线无法处理异或问题。因此，二维空间中一条直线的VC维是3.

二维空间中的超平面的VC维是3。更一般的，k维空间的超平面的VC维是k+1。

超平面的VC维与参数的数目相等。但这只是个巧合，事实上，模型的参数和模型的复杂度并没有必然的联系。例如，一个正弦曲线的VC维是正无穷大，但是它的参数只有3个。
$$f(x)=a\sin (bx+c)$$

最近邻分类器的VC维是无穷大的，因为无论你有多少数据点，你都能在训练集上得到完美的分类器。而当$\text{ 1-NN }\to \text{ K-NN }$,相当于减小了VC维。

一般来说，VC维越高，模型的分类能力更强，更flexible。但是VC维更多的是作为一个概念，实际上很难去计算一个模型的VC维。

---

---

回到刚才，经过前人推导，我们得到了一个测试集误差的上界如下：
$$E_{\text{test }}\le E_{\text{train }}+{\left(\frac{h+h\log (2N/h)-\log (p/4)}{N}\right)}^{\frac{1}{2}}$$
$\mathrm{N}=$ size of training set
$h=VC$ dimension of the model class
$p=$ upper bound on probability that this bound fails

从上式看，$$\text{ Good generalization }\to \text{ large }N\text{ and small }h$$
这是符合我们的直觉的。上面这个式子的推导很复杂，但是在实际中也没啥用，因为它给的上界太松了，一个很松的上界又有什么意义呢。

3、Hard-Margin SVM

对于上面这个两类分类问题，我们用直线进行分类，会发现有好多种分类方法。而SVM所选择的那条直线，是将Margin 最大化的直线。

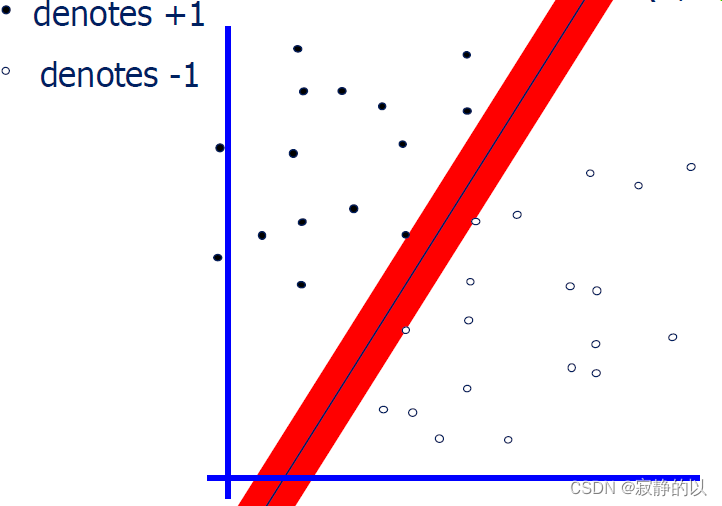
为什么要最大化Margin?

1. 直觉上感觉这最安全
2. 实际工作中确实不错
3. 当数据有小波动时错分的概率小一些
4. 模型只与support vector有关
   
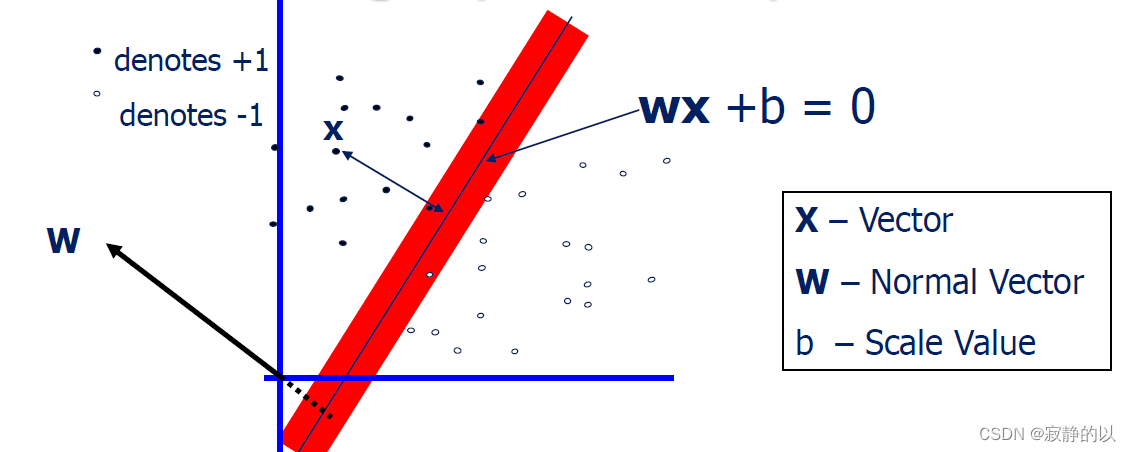
   点到直线的距离：
   $$d(\mathbf{x})=\frac{|\mathbf{x}\cdot \mathbf{w}+b|}{\sqrt{\Vert \mathbf{w}{\Vert }_2^2}}=\frac{|\mathbf{x}\cdot \mathbf{w}+b|}{\sqrt{{\sum }_{i=1}^d{w}_i^2}}$$
   定义Margin:
   $$\mathrm{margin}\equiv \underset{\mathbf{x}\in D}{\mathrm{argmin}}d(\mathbf{x})=\underset{\mathbf{x}\in D}{\mathrm{argmin}}\frac{|\mathbf{x}\cdot \mathbf{w}+b|}{\sqrt{{\sum }_{i=1}^d{w}_i^2}}$$
   所以我们就要考虑如何来最大化这个Margin了。

那么我们的问题就可以建模为：
$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmax}}\mathrm{margin}(\mathbf{w},b,D)\\ & =\underset{\mathbf{w},b}{\mathrm{argmax}}\underset{{\mathbf{x}}_i\in D}{\mathrm{argmin}}d\left({\mathbf{x}}_i\right)\\ & =\underset{\mathbf{w},b}{\mathrm{argmax}}\underset{{\mathbf{x}}_i\in D}{\mathrm{argmin}}\frac{\left|b+{\mathbf{x}}_i\cdot \mathbf{w}\right|}{\sqrt{{\sum }_{i=1}^d{w}_i^2}}\end{array}$$
如果只是这样的话，肯定是不行的，想像一下，一条直线离两类都非常远，也是符合上式的，因此需要附加条件，也就是直线能正确分类。
$$\begin{array}{c}\mathbf{W}{\mathbf{X}}_{\mathbf{i}}+b\ge 0\text{ iff }{y}_i=1\\ \mathbf{W}{\mathbf{X}}_{\mathbf{i}}+b\le 0\text{ iff }{y}_i=-1\\ y_i\left(\mathbf{W}{\mathbf{X}}_{\mathbf{i}}+b\right)\ge 0\end{array}$$
也就是
$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmax}}\underset{{\mathbf{x}}_i\in D}{\mathrm{argmin}}\frac{\left|b+{\mathbf{x}}_i\cdot \mathbf{w}\right|}{\sqrt{{\sum }_{i=1}^d{w}_i^2}}\\ & \text{ subject to }\forall {\mathbf{x}}_i\in D:y_i\left({\mathbf{x}}_i\cdot \mathbf{w}+b\right)\ge 0\end{array}$$
这边对一个限制条件进行强化，假设
$$\forall {\mathbf{x}}_i\in D:\left|b+{\mathbf{x}}_i\cdot \mathbf{w}\right|\ge 1$$
因为咱们是对w进行优化，所以本质上其实是一样的，就是一个缩放的问题。

那么对里层的优化，有：
$$\underset{{\mathbf{x}}_i\in D}{\mathrm{argmin}}\frac{\left|b+{\mathbf{x}}_i\cdot \mathbf{w}\right|}{\sqrt{{\sum }_{i=1}^d{w}_i^2}}\ge \underset{{\mathbf{x}}_i\in D}{\mathrm{argmin}}\frac{1}{\sqrt{{\sum }_{i=1}^d{w}_i^2}}=\frac{1}{\sqrt{{\sum }_{i=1}^d{w}_i^2}}$$

对于外层优化，只需最大化里层的下界就行，于是问题化为：
$$\begin{array}{rl}& \underset{\mathbf{w},b}{\mathrm{argmin}}\sum _{i=1}^d{w}_i^2\\ & \text{ subject to }\forall {\mathbf{x}}_i\in D:y_i\left({\mathbf{x}}_i\cdot \mathbf{w}+b\right)\ge 1\end{array}$$