A.1 高斯随机变量
A.1.1 标量实高斯随机变量
为一般高斯随机变量,
为标准高斯随机变量。则有:
- 标准高斯随机变量w的拖尾,定义为Q函数:
, 拖尾按指数律快速衰减
- 关系:
- 重要属性:线性变换不变性
A.1.2 实高斯随机矢量
- 标准高斯随机矢量的概率密度函数:
为原点到 w 的欧氏距离。
性质:(1)w经过正交变换O后,所得Ow也是标准高斯的。
(2)标准高斯随机矢量的概率密度函数具有各向同性。
(3)模的平方服从指数分布。
推论:(1)w在任何规范正交基下都服从相同的分布。
(2)从几何上看,w的分布对于旋转和反射具有不变性。
(3)标准高斯随机矢量在正交方向上的投影是相互独立的。
- 高斯随机矢量:
性质:(1)高斯随机矢量的任意线性变换也是高斯的。
(2)仅用协方差矩阵就可以表征
的密度。
当K为对角矩阵,即分量随机 变量互不相关时,高斯随机矢量由独立的高斯随机变量组成,称为白高斯随机矢量;当K为单位阵,为标准高斯随机矢量。
(3)一般而言,高斯随机矢量可以用均值和协方差矩阵K完全表征。
A.1.3 复高斯随机矢量
- 标量标准复随机变量
的实部和虚部为互相独立的、服从相同分布的N(0,1/2)的随机变量。
其实部、虚部均为实高斯随机矢量。复矢量
的均值、协方差矩阵、伪协方差矩阵包含相同的信息。
,
,
- 统计量由以下5个实参数确定:实部均值、方差;虚部均值、方差;实部虚部相关性。
- n维复高斯随机矢量
的实部和虚部可以构成2n维实高斯随机矢量。
- 循环对称性:
,若
与
具有相同的分布,则
为循环对称的。
- 循环对称高斯随机变量的性质:
(1) ,
,
确定循环对称复高斯随机矢量的全部统计量。因此,示为
;
(2)循环对称复高斯随机矢量的实部和虚部必须是独立同分布的零均值随机变量。
(3)PDF:。
(4)相位在[0,2π]上服从均匀分布;与模无关;模 服从瑞利分布,PDF:
; 模的平方
服从指数分布。
- 标准循环对称高斯随机矢量:
- 结论:AWGN:各向同性
A.2 高斯噪声环境下的检测
A.2.1 标量检测
最大似然接收机:发射uA和uB的概率相等时,若
则选择uA;否则选择uB。上式可简化为.即选择最邻近的信号。
A.2.2 矢量空间中的检测
接收矢量: ,
.
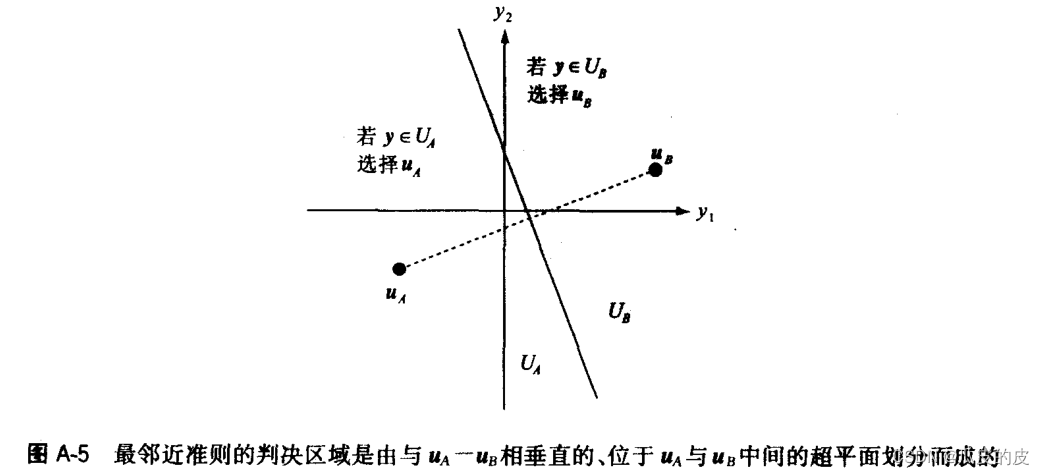
最邻近准则: 时输出uA.
- 从几何角度看,判决区域就是与矢量
垂直的超平面。当接收矢量位于与发射矢量相反的超平面一侧时,就会出现错误。
错误概率:, 其中
为矢量uA、uB到判决边界的距离。
- 将矢量检测转化为标量检测:
构造发射矢量 , 发送的信息为标量x,以等概率取±1/2。
发射码元x仅位于特定方向 上。
接收矢量在与v正交的方向上的分量为纯噪声,在v方向上的投影提供了检测所需的全部信息。
检测标量 ,由该式的第一个分量
, 即可对发射码元x进行判决。其中 ,
。
被称为接收矢量
的充分统计量,是接收信号在信号方向
上的投影,这一运算叫做匹配滤波器,即接收机中的线性滤波器与发射信号的方向“相匹配”。
差错概率 ,仅与两个星座点之间的有效距离
有关。
- 由二进制推广到M进制:M个发射矢量,矢量
在由
,…,
张成的子空间上的投影就是解决检测问题的充分统计量。
A.2.3 复矢量空间中的检测
标准加性复高斯噪声下, . 发射码元
以相等的概率取复矢量
与
之一。
.
类似地,令 ,发射矢量位于某一实维的子空间内。
接收矢量的复标量充分统计量
可以从的实部进一步提取充分统计量:
差错概率
- 共线信号下:例如发射PAM星座
发射信号 ,…,
共线,即对于某固定矢量
,
,
为复值且以相等的概率取每个星座点,则
在
方向上的投影
为充分统计量。注意,仅当星座点
为实数时,
才是充分统计量。
A.3 高斯噪声环境下的估计
A.3.1 标量估计
- 最小均方误差法估计x:
,
, x为零均值的实信号。
均方误差最小的估计值即经典的条件均值: 且
满足正交性:误差与观测时间无关
,故线性估计具有
的形式,最佳系数
可理解为用发射信号能量占接收能量的比例对y进行加权。
A.3.2 矢量估计
- 转化为标量估计:在
,
的条件下,由充分统计量
估计x
x的最佳线性估计为
等价于 ,
,
- MMSE外,还可以用SNR评价线性估计器。
当 (构成匹配滤波器)时等号成立。
结论:匹配滤波器会在任意线性滤波器的输出端得到最大的信噪比
A.3.3 复矢量空间中的均方估计
推广A.3.2的表达式,得到x的最佳线性估计为
,























 2316
2316











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








