informer之Proof of Lemma 1（引理1证明）M(q_i, K)

我们用详细的数学推导和结论证明了该不等式的正确性，我们将其分为两个部分进行讨论：不等式的左部分和右部分。

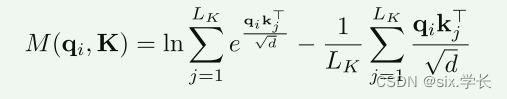
证明不等式：

$\ln LK\le M(q_i,K)\le {\max }_j\left\{\frac{q_i{k}_j^T}{\sqrt{d}}\right\}-\frac{1}{LK}{\sum }_{j=1}^{LK}\left\{\frac{q_i{k}_j^T}{\sqrt{d}}\right\}+\ln LK$

其中，$M(q_i,K)$定义为：

$M(q_i,K)=\ln \left({\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)\right)-\frac{1}{LK}{\sum }_{j=1}^{LK}\left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)$

左部分的解释

首先，我们看不等式的左部分。对于每一个查询向量$q_i$，第一个项$M(q_i,K)$是一个对数和指数函数，计算固定查询$q_i$和所有键的内积。我们定义：
$f_i(K)=\ln {\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)$

根据Log-sum-exp网络的相关理论（Calafiore, Gaubert和Possieri 2018）以及进一步的分析，函数$f_i(K)$是一个凸函数。此外，$f_i(K)$加上线性组合$k_j$使得$M(q_i,K)$成为固定查询情况下的凸函数。

然后，我们对单个向量$k_j$求导数：
$\frac{\partial M(q_i,K)}{\partial k_j}=\frac{\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)}{{\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)}\cdot \frac{q_i}{\sqrt{d}}-\frac{1}{LK}\cdot \frac{q_i}{\sqrt{d}}$

我们再将其整理为：
$\frac{\partial M(q_i,K)}{\partial k_j}=\left(\frac{\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)}{{\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)}-\frac{1}{LK}\right)\cdot \frac{q_i}{\sqrt{d}}$

最小值条件

为了找到该函数的最小值，我们需要让所有的导数为零，也就是令梯度为零：即：
$\frac{\partial M(q_i,K)}{\partial k_j}=0$

这要求：
$\frac{\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)}{{\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)}=\frac{1}{LK}$

这意味着：
$\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)=\frac{{\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)}{LK}$

对数化后，我们有：
$\frac{q_i{k}_j^T}{\sqrt{d}}=\ln \left(\frac{{\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)}{LK}\right)$

进一步化简：
$q_i{k}_j^T+\ln LK=\ln {\sum }_{j=1}^{LK}\exp \left(q_i{k}_j^T\right)$

由于所有的$k_j$对应的值是相同的，我们得到：
$k_1=k_2=\cdots =k_{LK}$

此时，最小值为：
$M(q_i,K)=\ln LK$

自然地，这需要$k_1=k_2=\cdots =k_{LK}$，我们有测量的最小值为$\ln LK$，即：
$M(q_i,K)\ge \ln LK$

证明不等式的右半部分

我们要证明不等式的右半部分，使用如下定义的$M(q_i,K)$：

$M(q_i,K)=\ln \left({\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)\right)-\frac{1}{LK}{\sum }_{j=1}^{LK}\left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)$

右半部分的证明步骤

根据图中的方法，我们逐步进行证明：

1. 定义最大内积：
   $\alpha ={\max }_j\left\{\frac{q_i{k}_j^T}{\sqrt{d}}\right\}$

2. 上界估计：
   ${\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)\le {\sum }_{j=1}^{LK}\exp (\alpha )=LK\cdot \exp (\alpha )$

3. 对数运算：
   $\ln \left({\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)\right)\le \ln \left(LK\cdot \exp (\alpha )\right)=\ln LK+\alpha$

4. 结合$M(q_i,K)$的定义：

   我们有：
   $M(q_i,K)=\ln \left({\sum }_{j=1}^{LK}\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)\right)-\frac{1}{LK}{\sum }_{j=1}^{LK}\left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)$

   使用第3步的结果：
   $M(q_i,K)\le \ln LK+\alpha -\frac{1}{LK}{\sum }_{j=1}^{LK}\left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)$

   由于$\alpha$是定义的最大值：
   $\alpha ={\max }_j\left\{\frac{q_i{k}_j^T}{\sqrt{d}}\right\}$

5. 最终表达式：
   将$\alpha$替换回表达式中，得到：
   $M(q_i,K)\le \ln LK+{\max }_j\left\{\frac{q_i{k}_j^T}{\sqrt{d}}\right\}-\frac{1}{LK}{\sum }_{j=1}^{LK}\left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)$

最终结论

综上所述，我们已经证明了不等式的右半部分：
$M(q_i,K)\le {\max }_j\left\{\frac{q_i{k}_j^T}{\sqrt{d}}\right\}-\frac{1}{LK}{\sum }_{j=1}^{LK}\left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)+\ln LK$

因此，引理1的右半部分不等式得证。

举例说明

假设有一个查询向量$q_i$和一个键集合 K = { k 1 , k 2 , … , k L K } K = \{k_1, k_2, \ldots, k_{LK}\} K={k1​,k2​,…,kLK​}。假设$d=1$并且每个键向量$k_j$都是相同的向量$k$。此时，$q_i$和每个键的内积相同，即$q_i{k}^T$。根据以上推导：

• 对于左部分，因为所有$k_j$都相同，所以$\exp \left(\frac{q_i{k}_j^T}{\sqrt{d}}\right)$的和为$LK\cdot \exp \left(\frac{q_i{k}^T}{\sqrt{d}}\right)$，对数之后得到$\ln LK+\frac{q_i{k}^T}{\sqrt{d}}$。
• 对于右部分，选择最大的内积（其实就是$q_i{k}^T$），所以不等式右侧为$\ln LK+\max \left\{\frac{q_i{k}_j^T}{\sqrt{d}}\right\}$，因为所有的内积都相同，所以最大值也是$\frac{q_i{k}^T}{\sqrt{d}}$。

这样，通过具体的例子说明，不等式的左右两部分在不同情况下如何达到平衡，从而证明了不等式的正确性。