机器学习之覆盖算法

总述

覆盖算法的核心：找到一条规则，覆盖尽可能多的正例，排斥尽可能多的反例。主要介绍三种方法：（1）AQ15（洪家荣改进的）；（2）AE（洪家荣）；（3）FCV
后续有许多对覆盖算法的改进，主要目的是找到更简洁的规则，满足正例，排斥反例，以减小计算量
**NOTICE：使用数量最少的规则，覆盖所有正例，排斥所有反例，是NP问题。**

一、AQ15

1. 公式

针对每个正例ei，规则为：eiV¬NE 即：eiV¬（e1-˅…˅ek-）≡ ei V（¬e1-˄…˄¬ek-），通过逻辑运算，最后得到的结论，即覆盖正例ei，排斥所有的反例，即NE。

2. 举例（计算第一个正例的规则）

根据第一个正例得到的规则如下：👇

这条规则满足第一个正例，排斥所有的反例，具有泛化能力，但计算量很大，因此后续需要优化。

2. 扩张矩阵算法AE

3. FCV算法

PE‘= PE； NE’= NE
step1： 建立PE的评价矩阵PEM和NE的评价矩阵NEM；
step2：For( i =0; i< N; i++)
            For(j=0; j<F; j++) 
                求PEM[i,j]/NEM[i,j]最小值；
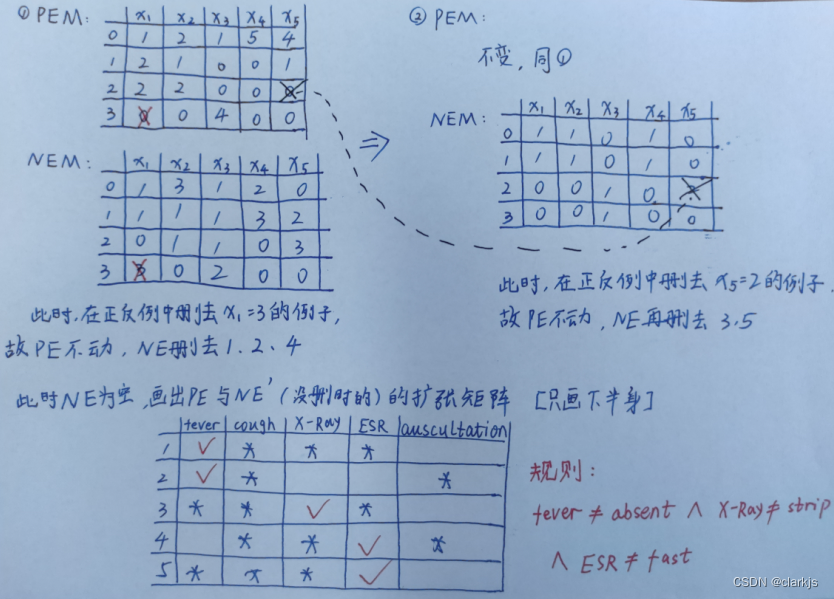
Step3：在PE和NE中删除第j个属性的取值为i的例子；
Step4：如果NE不空，重复Step1；否则建立PE在NE'的扩张矩阵EM，寻找一个公共路径，即覆盖规则；
PE‘=PE’-PE； PE=PE‘；  NE=NE’；
重复上面步骤，直到PE’为空，即得到覆盖正例集PE，排斥反例集NE的所有覆盖规则

将属性的每个取值数值化，0，1，2自己编，如下👇：


然后，分别构造正例集的评价矩阵和反例集的评价矩阵。按顺序执行上面的步骤，本例题的步骤如下（自己写的，不一定对奥，欢迎大噶指出错误一起讨论~）：👇