【机器学习微积分】01 见微知著：导数与微分

1.函数的连续性

1.1.函数在单点处的连续性

从这一讲开始，我们正式进入到微积分的部分中来。我们首先从函数的连续性开始讨论，然后逐步过渡到切线和导数的概念。

函数 f ( x ) f(x) f(x)在具体的取值点 c c c点是否连续，我们针对性的来看下面三幅图中的具体情形：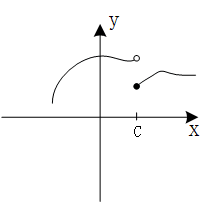

在这幅图中，我们发现在点 c c c处，函数的左极限和右极限不相等，即 l i m x → c − f ( x ) ≠ l i m x → c + f ( x ) lim_{x\rightarrow c^{-}}f(x) \neq lim_{x\rightarrow c^{+}}f(x) limx→c−​f(x)​=limx→c+​f(x)，因此 l i m x → c f ( x ) lim_{x\rightarrow c}f(x) limx→c​f(x)不存在， c c c点处函数的极限不存在，因此函数 f ( x ) f(x) f(x)在点 c c c处不连续。

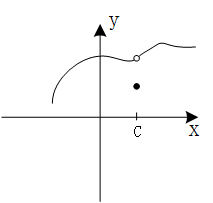
这幅图中情况似乎要稍微好点儿，我们发现 l i m x → c − f ( x ) = l i m x → c + f ( x ) lim_{x\rightarrow c^{-}}f(x)=lim_{x\rightarrow c^{+}}f(x) limx→c−​f(x)=limx→c+​f(x)，函数 f ( x ) f(x) f(x)在 c c c点处的极限是存在的，但是从图中可以看出，函数的极限值和 c c c点处函数的实际取值不相等，即： l i m x → c f ( x ) ≠ f ( c ) lim_{x\rightarrow c}f(x) \neq f(c) limx→c​f(x)​=f(c)，因此函数 f ( x ) f(x) f(x)在点 c c c处仍然不连续。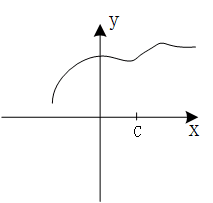

这幅图中以上出现的两个问题都不存在了，我们看到：一方面函数 f ( x ) f(x) f(x)的极限是存在的，而另一方面 l i m x → c f ( x ) = f ( c ) lim_{x\rightarrow c}f(x)=f(c) limx→c​f(x)=f(c)，点 c c c处的极限和函数的取值又是相等的，因此在这幅图中，函数 f ( x ) f(x) f(x)在点 c c c处是连续的。

那么，依照严格的定义，对于一个定义在包含点 c c c的区间上的函数 f ( x ) f(x) f(x)，如果 l i m x → c f ( x ) = f ( c ) lim_{x\rightarrow c}f(x)=f(c) limx→c​f(x)=f(c)成立，则称函数 f f f在点 c c c处连续。

1.2.函数在区间上的连续性

进一步扩展到区间上，如果函数 f ( x ) f(x) f(x)在开区间上的任意一点连续，那么这个函数 f ( x ) f(x) f(x)就在整个这个开区间上连续。

如果谈到闭区间 [ a , b ] [a,b] [a,b]上的连续性问题，那么就需要着重单独讨论区间的左右两个端点：我们首先从右侧逼近左侧端点 a a a，如果 l i m x → a + f ( x ) = f ( a ) lim_{x\rightarrow a^{+}}f(x) =f(a) limx→a+​f(x)=f(a)成立，则称函数 f ( x ) f(x) f(x)在端点 a a a上右连续，我们再从左侧逼近右侧端点 b b b，即 l i m x → b − f ( x ) = f ( b ) lim_{x\rightarrow b^{-}}f(x) =f(b) limx→b−​f(x)=f(b)成立，则称函数 f ( x ) f(x) f(x)在端点 b b b上右连续。

那么，如果函数在开区间 ( a , b ) (a,b) (a,b)上连续，且在左侧端点 a a a上右连续，在右侧端点 b b b上左连续，此时此刻，我们就能够说函数 f ( x ) f(x) f(x)在闭区间 [ a , b ] [a,b] [a,b]上是连续的。

2.关于切线

切线是一个大家都非常熟悉的概念，什么是切线？有一种说法是一条曲线的切线只与这条曲线有一个交点。这个概念有很大的局限性，他只对圆环类的曲线有效，而对例如下面的这条曲线，描述显然就不适用了：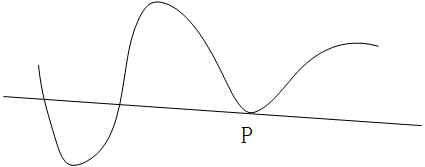

实际上，在上面这幅图中，直线显然是曲线在 P P P点处的切线，但是更明显的是，这条直线与曲线的交点数不止一个。那么我们应该怎样更准确的描述切线呢ÿ