固体物理 2022.10.4

凉月松心

已于 2022-10-04 09:50:33 修改

阅读量692

点赞数

分类专栏：固体物理文章标签：制造

于 2022-10-04 08:50:06 首次发布

本文链接：https://blog.csdn.net/m0_52555753/article/details/127158817

版权

固体物理专栏收录该内容

25 篇文章 8 订阅

订阅专栏

作业回顾：

1.详细步骤

2.物理列式计算

重点研究纵波，横波看作另一个晶向上的纵波，这样子可以简化我们的计算（重点研究沿着单原子链的方向）

通过泰勒展开，我们可以得到

这个关系就像一个回复力的形式

这是在a附近的一个微分量，所以前面的系数是一个常数

我们按照顺序来写， $\small \beta_2-\beta_1=-\beta(u_n-u_{n-1})+\beta(u_{n+1}-u_n)=-\beta(u_{n+1}+u_{n-1}-2u_n)$

然后就可以得到合力

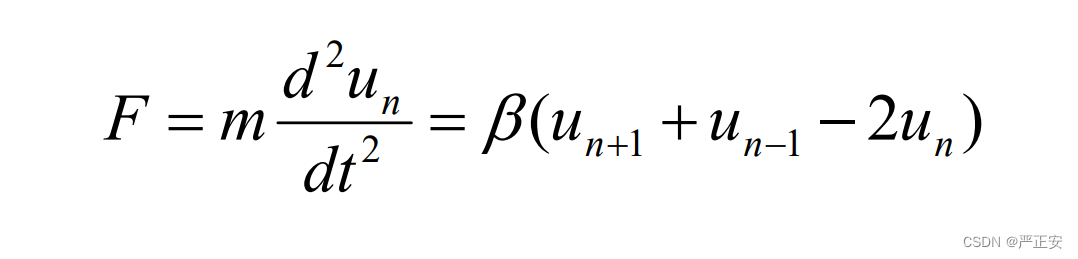
m是原子质量，对势能的二次微分量就是加速度

有了力学方程，我们就可以进行求解了

对于偏微分方程的求解，一个很重要的问题是我们如何确定边界条件？

《数学物理方法》介绍的是各种微分方程的求解方法

一个是求解的方式，另一个是如何进行边界条件界定，在这道题里面我们要引入一个思想：我们在考虑单原子链上的原子的时候，我们认为是相同的，没有特殊的Atom，在第七讲中，我们讲势能计算的时候，我们其实也遇到过边界的问题，边界的Atom和中心的Atom没有本质的区别，从纳米材料的角度来说，表面的原子数量比较多，然后就有很多奇特的物理化学性能，还有其他很多的光学性质，电学性质，在Atom数量比较大的时候，边界的占比就会减少，此时我们不是在纳米尺度，更多Atom是包括在中间的，我们在这个里面，用到的是一个周期性的边界条件，对于一维单原子链来书

我们可以有很多个Atom，不管怎么画，总有两个Atom在两个端点处，我们如何处理边界的两个Atom，有n个Atom就会有n个这样的力学方程

对于边界上的Atom，照我们原来的处理思路来说，需要额外研究一个新的情况，为了让情况简化，我们用了周期性的边界条件（实际上如果是一条单原子链的话，边界的两个肯定和中心的不一样），我们这里用了波恩-冯卡曼边界条件，当Atom数量比较多的时候，我们可以用周期性条件来近似（第一个近似是最近邻近似）,第二个就是此处的周期性条件近似

如何理解周期性边界条件？

我们把边上的Atom，再往下画，画成一个圈，这个就是波恩-冯卡曼条件的精髓，把直线型画成闭环的圈型，如果用一个数学公式来理解的话， $\small X_{n+N}=X_{n}$ ,n+N号原子核n号原子保持相同的运动

用了这个近似条件之后，我们就可以忽略一维单原子链，所有的Atom如果转了N个，就会回到原先的位置

我们如果直接求解的话，将会有N个方程

二次微分方程具有一般性的求根公式， $\small u_n=Ae^{i(nka-\omega t)}$ ,这就是一个波动方程的形式 $\small e^{i(kx-\omega t)}$

k表示波向前运动的能力，x代表一维，wt是随着时间变化的一个情况

波不仅可以沿着X方向运动，有这个运动的快慢，同时随着时间也会有一个原地的一个振动，有两种引起波变化的值，一个是原地的振动，一个是向前的一个运动，都可以在我们这个公式中体现出来，整体上 $\small kx-\omega t$ 都叫做相位（phase），我们把通解代入到微分方程中

代入之前观察一下性质 $\small u_{n`}=u_n e^{ika(n`-n)}$ ，这是一个比较关键的性质

我们不用计算每一个Atom的变化，我们立足于整体，整个单原子链如何运动？

通过通用的求根公式，我们就可以把他们整个链接起来，形成一个有规律的整体

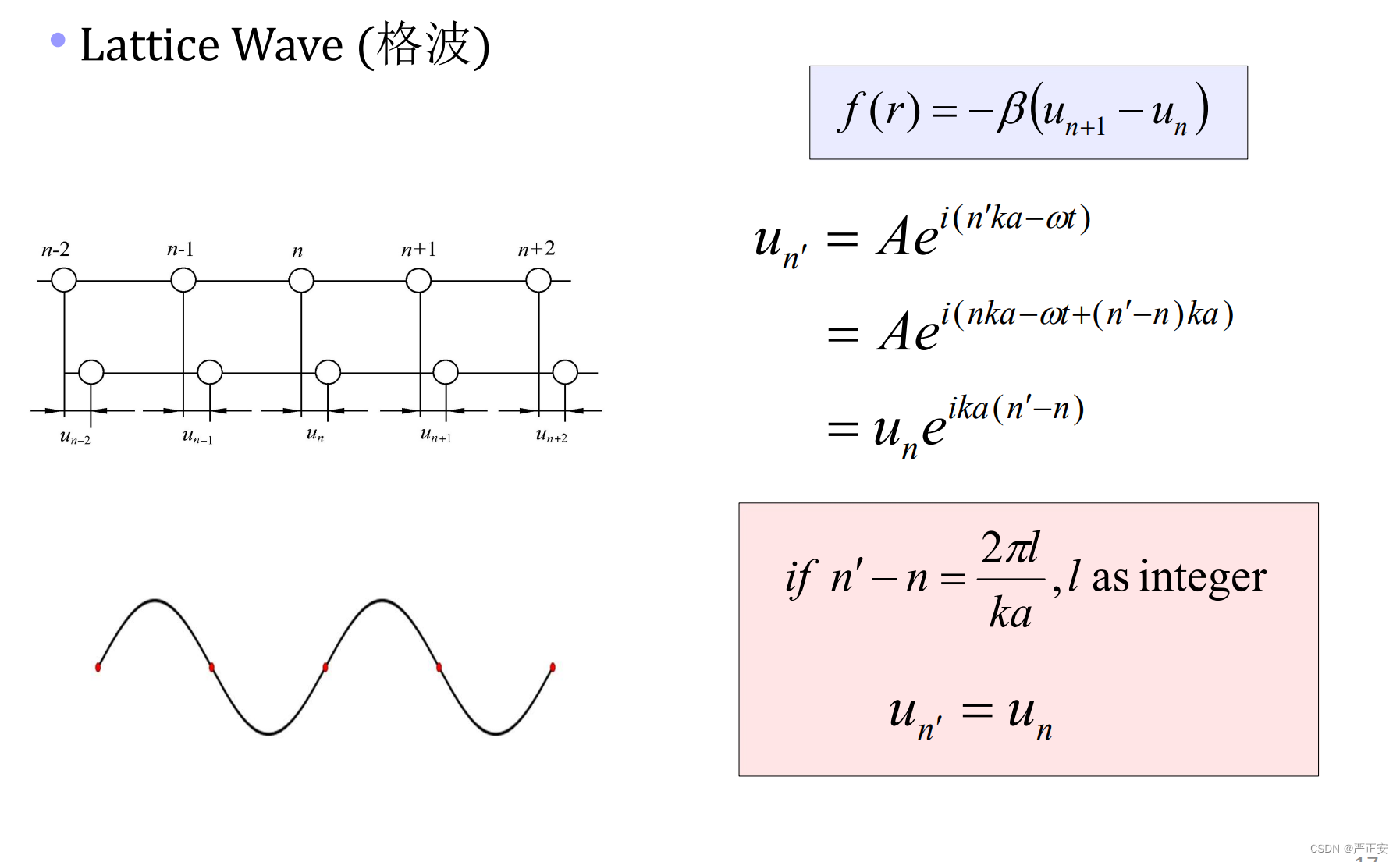
在这个链里面，存在着一些原子，他们的位移变化是相同的,比如上面有N个Atom，如果满足上面的关系的话 $\small (n`-n)ka=2 \pi l$

除了相同之外，我们还可以得到相反，如果是奇数倍的话

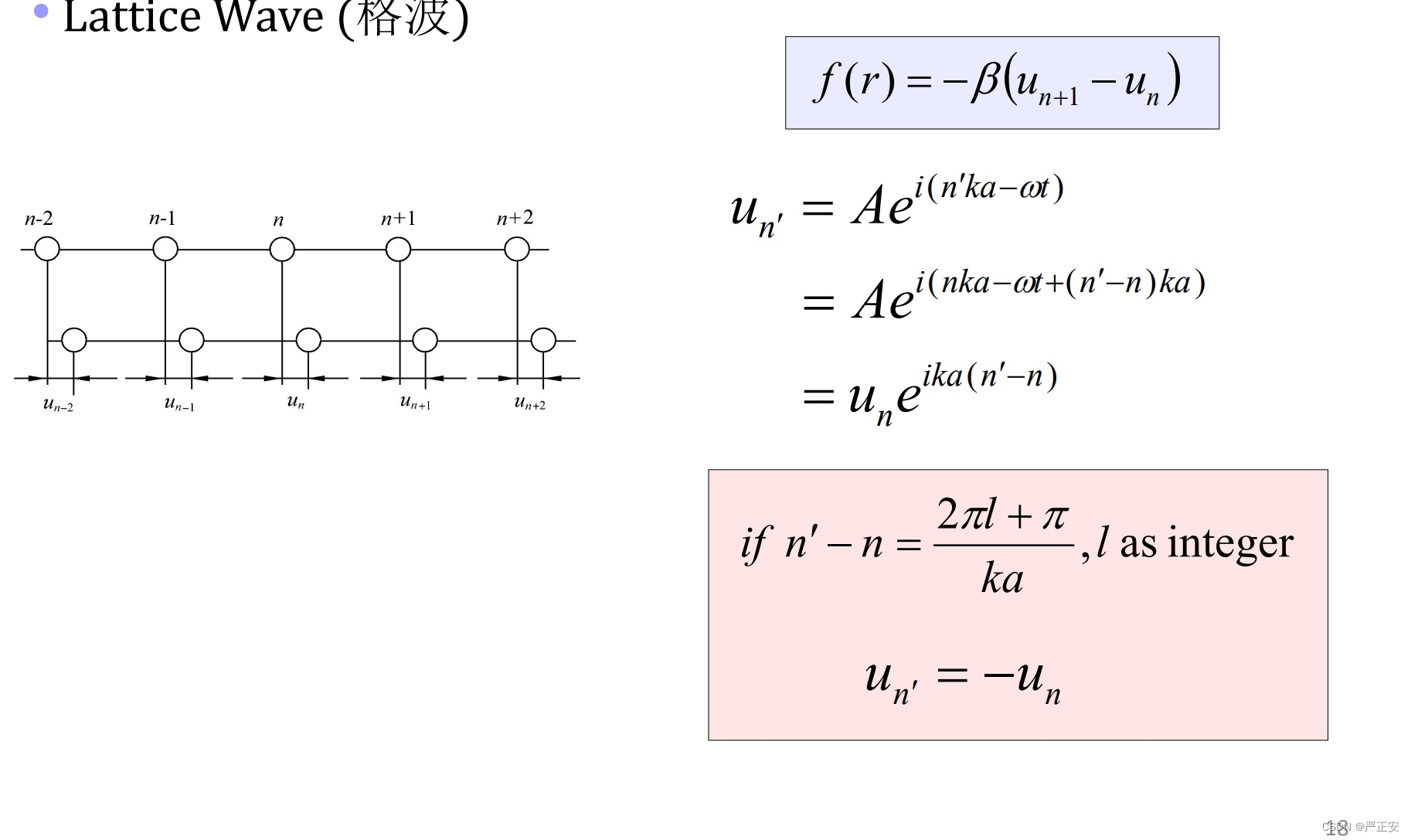
可以看出来不同的Atom的位移之间，有一种从小到大，再从大到小的一种位移关系，就形成了一种类似波动的形式（位移在不同atom上形成一种波动形式，我们所说的格波，就描述的是这么一个形式）

Lattice Wave 形容的是位移在不同原子之间的一个关系，形成了一种类似波动的关系，每一个Atom的大小，都跟它们之间的距离有关系，这样的话就把所有的Atom链接起来了，这号原子的位移，要受到所有其他Atom对它的影响，只能符合这么i一个倍数关系

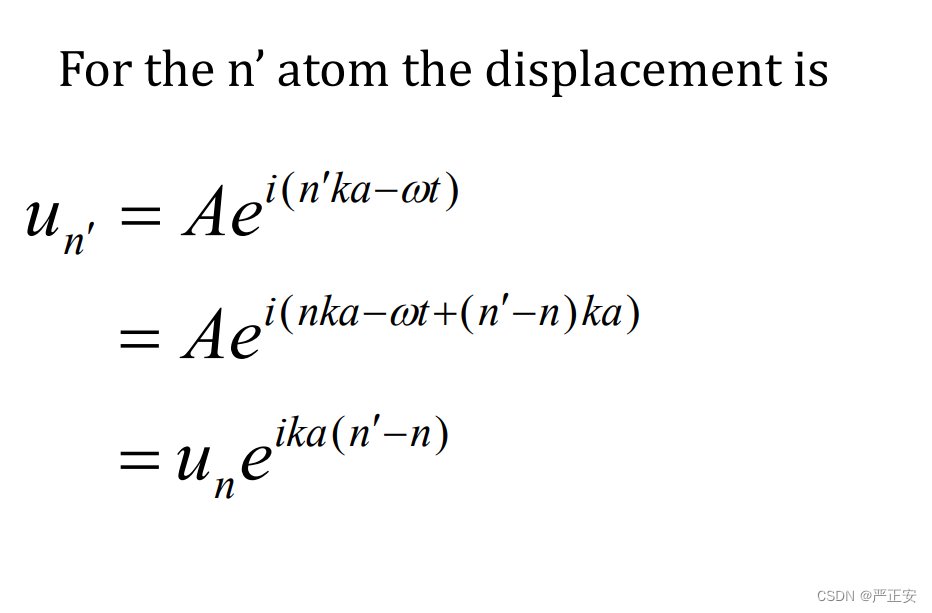
这种波称为Lattice Wave，不是独立存在的，没有那么自由，受到周围原子的影响

位移呈现一种周期性变化，这种运动形式称为格波

K可以认为是格波的波矢，显示的是格波向前运动的能力，过了一会，可能就会翻转过来，呈现出一种运动的状态，这种翻转的速度，可以认为是由K来决定的

则有点像，我们看体育比赛的时候的观众所呈现出的波浪的欢呼

这是关于通解的一些性质，有了这些性质，就可以更好的去定义格波

因为我们知道每个原子之间振幅的联系，公式左边是对时间进行微分，时间微分他会出来一个平方的形式，代入可以知道，左右两边都有一个 $\small u_n$ 然后就可以消去，得到我们课件中的这个公式 $\small \omega^{2}=\frac{2\beta}{m}[1-cos(ka)]$ (Sin项，利用欧拉公式，自然而然就消掉了)

这样的话，我们就得到了 $\small \omega ^{2}$ 和K之间的关系，这里面的关系就是w和k之间的关系

$\small \omega ~ k$ 之间的关系，我们称之为色散关系(dispersion)

我们在固体物理里面，会有很多色散关系，每一种色散关系，都是 $\small \omega ~ k$ 之间的关系，凡是有波的时候，都可能有色散关系（一维单原子链的振动，可以认为是机械波）

我们后面还会学到电磁波，在固体中电磁波的色散关系，以及核外电子的色散关系，能带关系

它代表的含义是，不同频率的波传播的速度和能力是不一样的

$\small \omega$ 是波的频率， $\small k$ 是波矢，代表了波向前传播的能力

一般情况下，振动比较慢的波，传的比较远，我们知道有短波电台和长波电台

一般短波电台传的不是特别好，需要在短的范围内进行使用，长波电台可能几千公里之外，还可以听到（长波传的比较远）短波和长波就是形容频率的，长波频率小，短波频率大，穿的近就是k比较大，传的远就是k比较小，他们之间满足一定的关系

色散关系会贯穿所有波，不管是声波，电磁波，还是核外电子的概率波，都有色散关系

我们对色散关系进行简单的化简，用二倍角公式进行化简

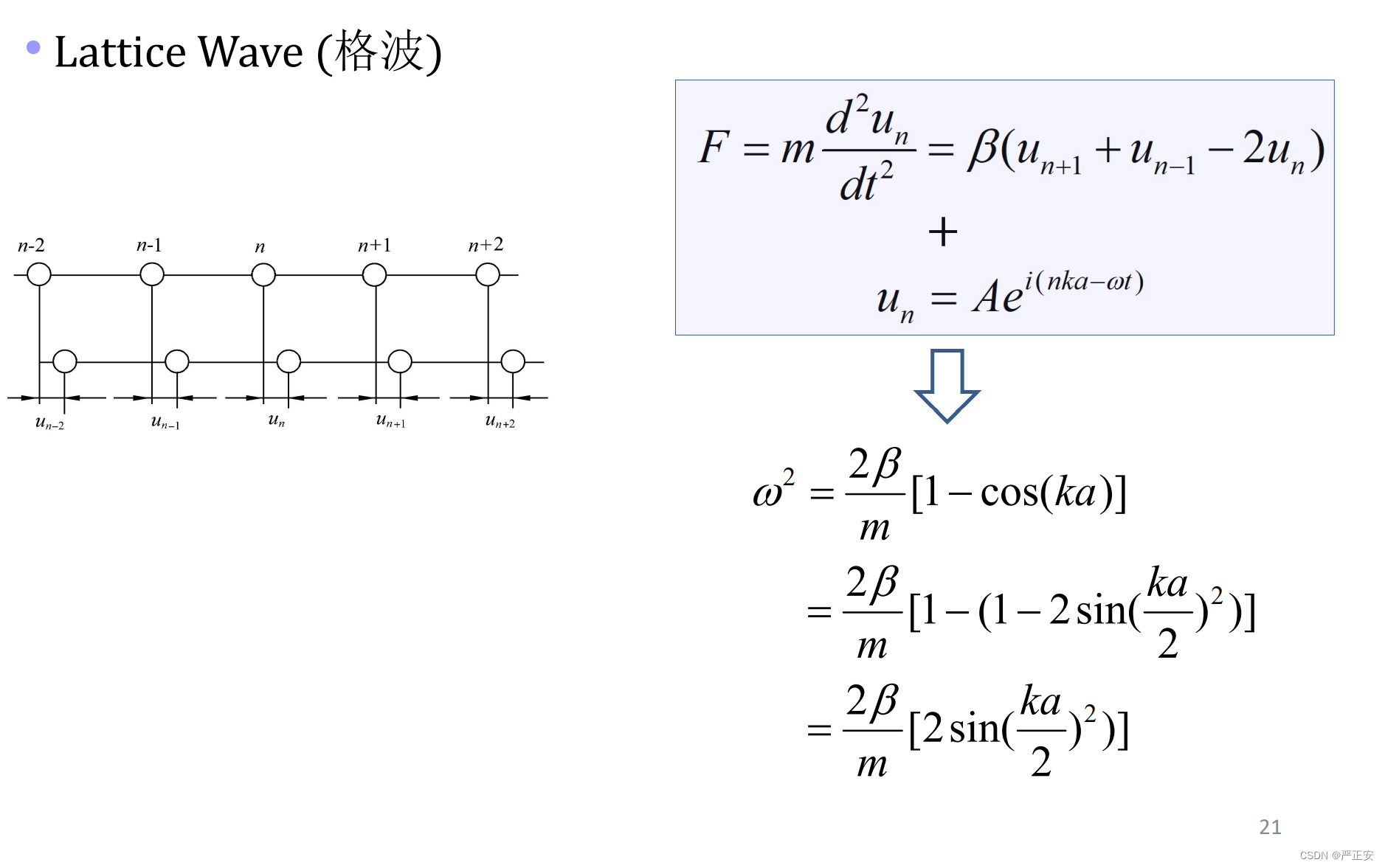
这样的话，便于我们开方

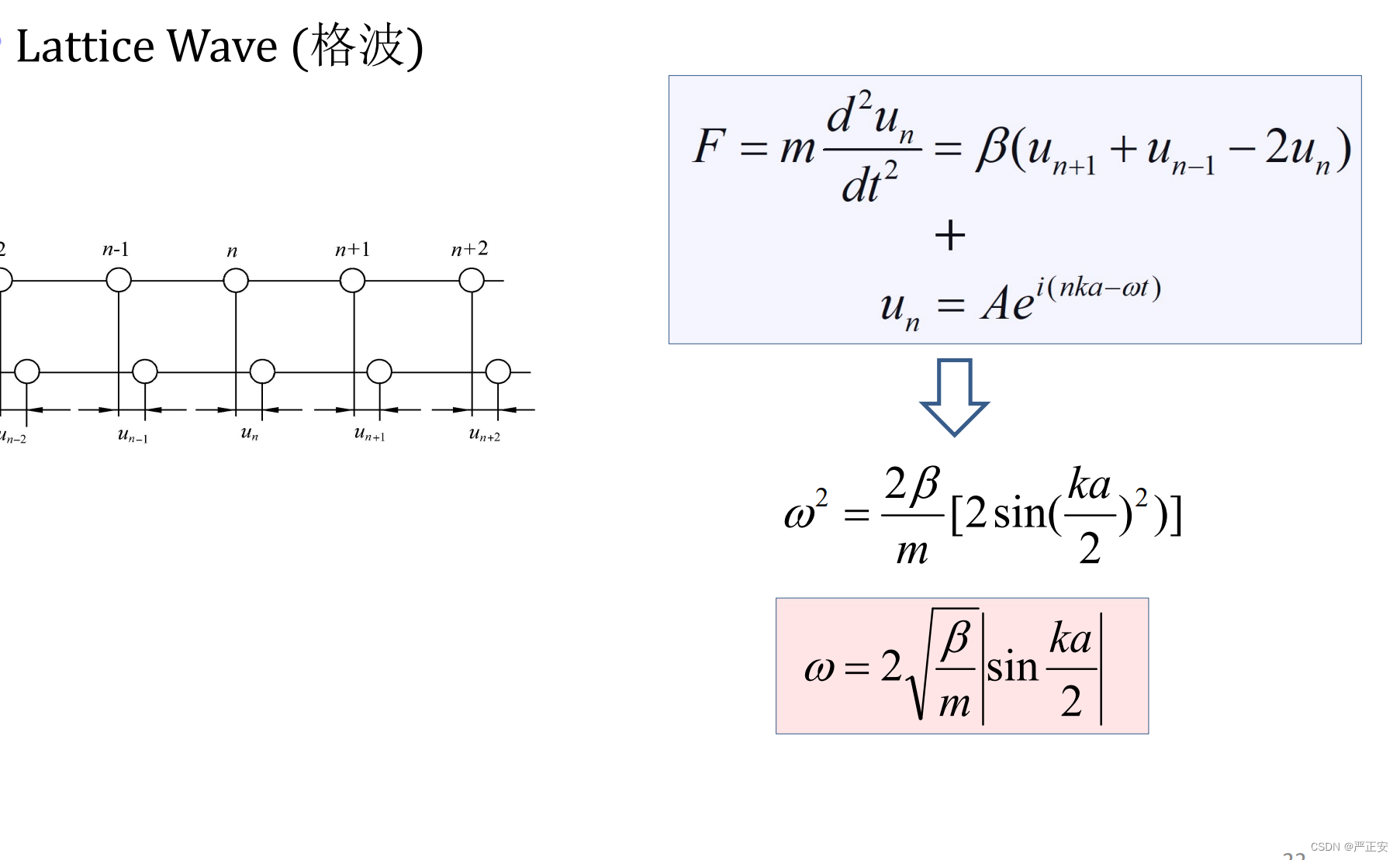
在实际的应用中 $\small \omega$ 是不存在负的值的，数学中才可能看到负的频率

这样的话，就是 $\small k=\frac{2\pi}{a}$ ,就是我们倒格空间的lattice contant（倒格空间的基矢），周期对于K来讲，是倒格空间的基矢大小，这是一个非常有意思的现象，到最后会发现，单原子链的振动，摆动是有周期的，K是有周期的，K是倒格空间的基矢大小

我们把图画出来

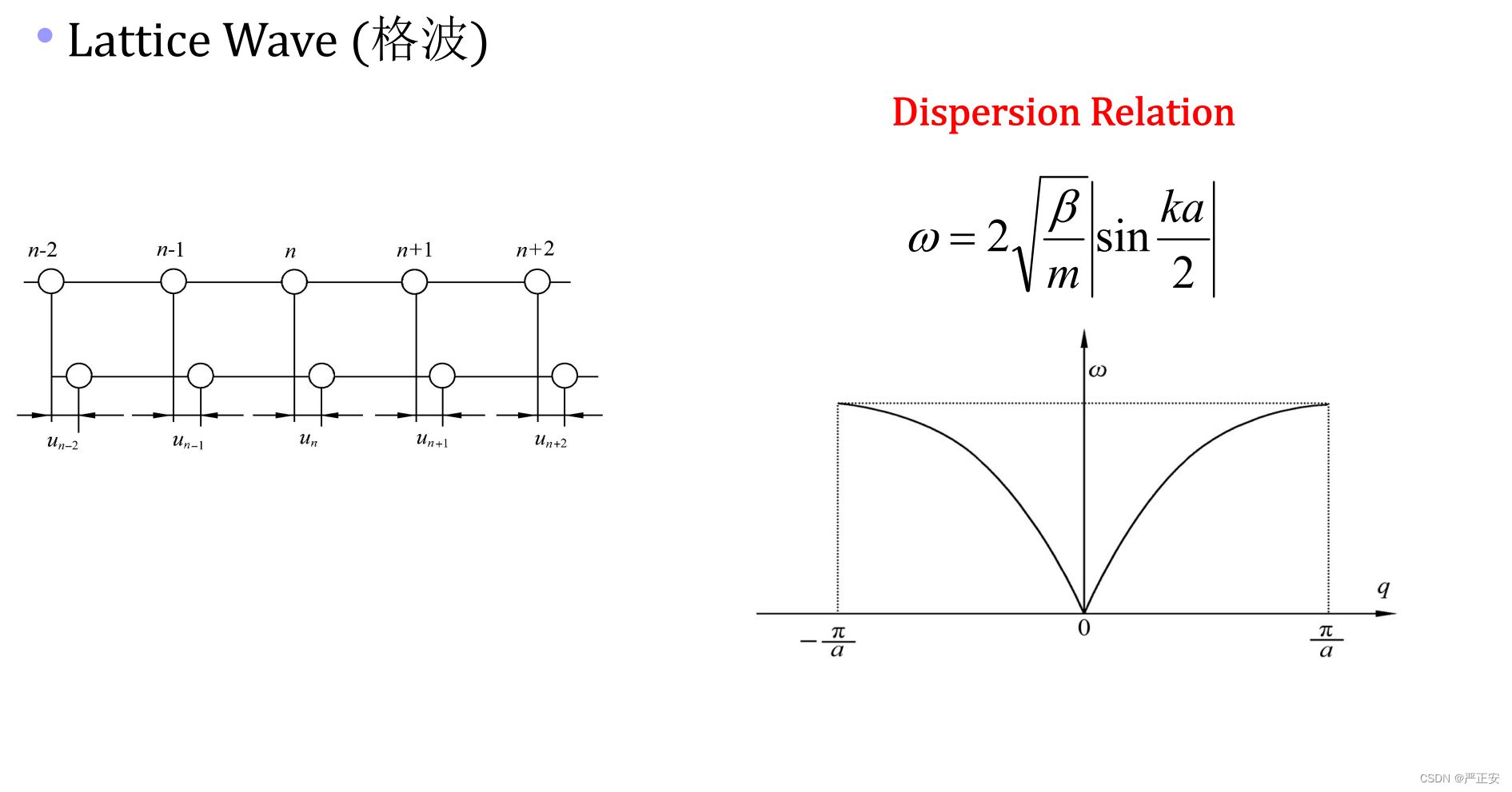
这个是我们最后得到的w k的关系图，绝对值之后，我们把下面这一只反过来，在这个里面，我们已经知道K是有周期性的， $\small \frac{2 \pi}{a}$ ，这样的话就可以定在一个周期里面，关于K=0对称，这样一个最简单的一个周期

这里面需要注意的是，实际在应用中，也没有这么绝对的定义

对K的取值范围，这是书上严格的定义，这是我们关于画出色散关系的第一个周期

第一个周期，我们称之为第一布里渊区（画色散关系的第一个区间）

其实还可以画第二个，再往外画，就到第二布里渊区了

我们在这个里面，色散关系比较简单，所以只画第一布里渊区就可以了，半导体物理中能带关系也就是w和k之间的关系，因为w可以化作能量的形式 $\small h\omega=E$ ,能带关系本质上还是w-k关系，对于电子的色散关系，只是把w换成了能量（第一布里渊区的图，需要大家会画）有些书里面也把这个k定义为q， $\small k->q$