AI画画近期貌似挺火的,也出了不少有趣的作品,甚至闹出了一些轰动的趣事。对此我也惊讶现在的科技都这么发达了么,岂不是可以满足我各种奇奇怪怪的想法[doge]?当然做学问嘛,我们也要知其然并知其所以然,因此我也是怀着好奇的心看了一些有关Diffusion model的论文,以及一些博客视频等,在此汇总一下,并说一下自己的看法。
其实扩散模型(diffusion model)很早之前就有人提出来过,但是开始变得火热还是起源2020年,尤其是DDPM(Denoising Diffusion Probabilistic Models)的提出,更是掀起了热潮。本文将对DDPM这篇论文进行粗略的解读,并对其中的一些公式推导进行演算,可能有不对的地方,希望大家见谅。
要想了解扩散模型,我们得先对生成模型有个感性的认识。对于一个生成模型来说,我们希望给定它样本,让它知道这些样本大致是什么分布,这里记作
,然后自己产出的一个分布
去无限的接近
,这样我们就可以通过不断的采样来获得样本中的见过的样本,以及没见过的样本。这可能有点抽象,这里举一个简单的例子:假如现在我们有这样几个矩形的样本(如下图所示),这六个矩形构成了一整个样本X,每一个就是
。

为了简化表示这几个矩形,我们采用它们的左上角坐标、长、宽来表示每一个样本x,即,这样我们只要知道左侧的这个四维向量就能知道这个矩形大致长什么样了。并且我们观察给我们的样本X,发现正方形出现的概率是很大的(下面四个都是),这说明样本中,长宽相等出现的概率是最大的!这样我们采用极大似然法对样本矩形的长宽(不考虑坐标了)进行一个概率分布拟合,就大致得出下图这样的概率分布
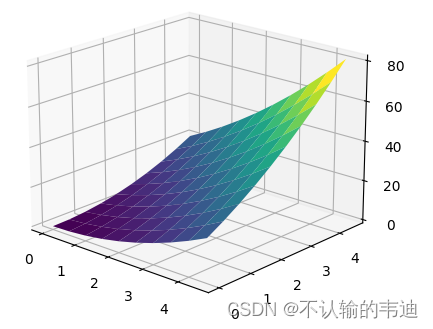
从图上我们大致可以看到从左下到右上的值是很高的,这对应了长宽相等出现的概率很高的这个样本得出的知识;也就是说,我们完全可以推断,这个概率分布与真实的概率分布相差不大,因此我们可以在这个分布上任意采样(比方得到长3宽3、长2宽3...),这样我们就可以得到和给定样本不一样的矩形。
从上面的例子我们可以发现两点有趣的地方:1、我们将图像(矩形)这个高维的东西转成了只有四维的向量,但是这个是比较简单的例子,如果是一张风景画,我们还怎么将其变成低维的向量呢?2、我们得出的概率分布太粗略了,感觉是接近,但也只是感觉,有什么办法比较我们推理得到的概率分布与真实的概率分布是否接近呢?对于这两个问题,倒不是扩散模型的重点,有兴趣的朋友可以看看VAE的知识。无论如何,我们至少对生成模型有了一个比较感性的认识,就是让模型学习样本然后自己diy一个不存在的新东西。
去噪的扩散概率模型(Denoising Diffusion Probabilistic Models)
本文要讲的DDPM倒还没有具备生成新东西的能力,它与AutoEncoder一样,将原样本变成一个完全看不出与原样本有任何联系的东西,然后再把这个没有任何联系的东西在还原成原样本。但与AutoEncoder不同的是,diffusion model不是将高维图像编码成一个低维的向量,而是将原始图片不断进行加噪加噪加噪,让它最终变成一个全是噪声的图片。这显然与自编码器一样变态,好好的图片把它折腾成这亚子;但是difussion model却比AutoEncoder要好的是,它是在像素级上进行操作,因此会保留很大的信息;而自编码器将图片编码成低维难免会损失很大的信息,因此像VAE这样的模型,生成的图片质量不是很清晰。
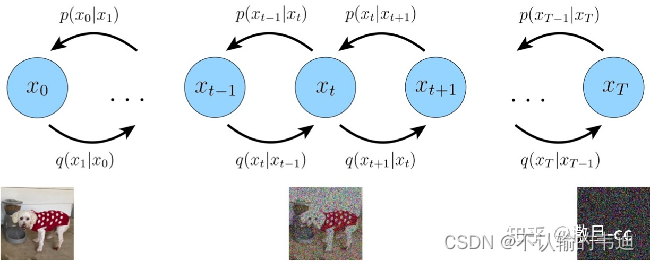
(这里放上知乎大佬的图,DDPM的流程大致如图所示)
既然DDPM与自编码器有点类似,那么它就会包括两个过程:1、将原图变成一个莫名其妙的东西(扩散过程)。2、将这个莫名其妙的东西在还原一下(逆扩散过程)。
DDPM扩散过程
已知一个样本服从分布
,在任意时刻
,我们往这个样本添加噪声,这个噪声服从一个与当前样本
以及一个常数
有关的高斯分布,即
。那么在
时刻应该有如下等式:
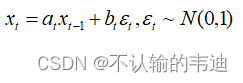
上式给的有点突然,这里详细说明一下。首先先给一个采样的tips:
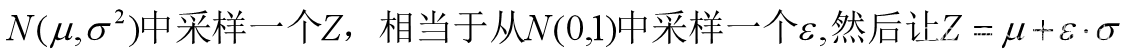
假设时刻的噪声服从这样的高斯分布
,显然这个符合上面的条件,那么这个噪声采样于这个分布,根据上述的tips就有
,稍加变形就是上面的等式。这样我们就得到了在扩散过程中,后一个样本
与前一个样本
关系的显式表达。注意到扩散过程是一个加噪的过程,因此后面样本的信息量将少于前面一个样本,因此式子中的
是一个不断衰减的数,而
我们暂且不关心。并且这是一个马尔科夫链过程,下一个时刻只受到这一时刻影响。我们将上式不断地展开就能得到

这就给出了每一个时刻的样本与原始样本
之间的关系,并且注意到红框内的式子,每一项都是独立的高斯分布,根据高斯分布的可加性,我们有红框内服从
,因此再次使用我们的tips,就可以把上式化简为:
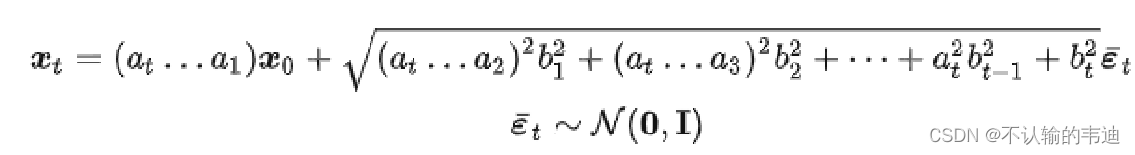
但是这个式子又臭又长,我们能不能简化它呢?我们注意到将前面的系数与根号内的式子做一个运算:

如果我们人为设定 那么上面这么长的式子直接就化简为1!这是一个非常好的事情,因为我们知道了
和
都是绝对值小于1的,并且
与
的关系可以化简为:
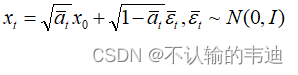
其中。要知道,每一个
都是我们人为设定的衰减的常数,因此,我们可以任意地获得
时刻的样本。
DDPM逆扩散过程
上面的扩散过程刻画了样本的变化的过程,其中我们知道了只需设定一组衰减的(0,1)范围内的数a,就可以任意得到t时刻的样本。我们将上文的一个公式进行变化(注意和
的区别):

样本到
的关系公式其实刻画了一个这样的采样过程:
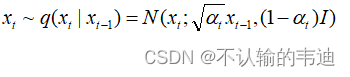
既然扩散过程是从一个已知参数的高斯分布中采样的过程,那么很合理地我们假设逆扩散过程也是一个从高斯分布中采样的过程,即

注意由于逆扩散过程是很困难的,找不到任何好的办法,因此我们采用神经网络去拟合,因此公式中的其实就是神经网络的参数。那么和扩散过程一样,我们根据马尔科夫链将上式改写成:
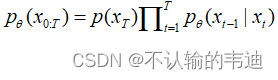
此时我们仅知道(其实就是全是高斯噪声的噪声图片),直接求
是很困难的,因此我们退而求其次,去计算
(因为根据马尔科夫链,这个和上面那个其实是差不多的),也就是给定
和
,去求
的概率;并且在扩散过程中我们知道
,再次根据我们的tips,可以有
这样就有(此时):
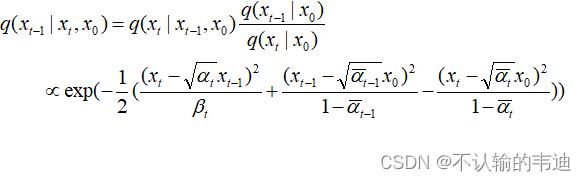
这很像一个高斯分布的表达式,为此我们将凑出来这样的表达式,并且知道了
和
分别可以表示成:

甚至可以根据上文和
之间的关系,将
再次简化为如上式那样。到这里我们也就知道了逆扩散过程大致应该也是一个从一个高斯分布中采样的过程,然后我们就可以设计神经网络了。但介于我能理解有限,大家可以去看这个和这个的对后续处理的讲解,上面的一些推导也是大致来源于他们。
我理解不是很透彻,上面的公式可能存在一些错误,望大佬们批评指正!





















 1322
1322











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








