区别：p 范数、椭圆范数、m1 范数、Frobenius 范数、 m∞ 范数、矩阵1范数、矩阵2范数、矩阵∞ 范数、矩阵M范数、矩阵G范数

勤劳的进取家

已于 2025-04-01 10:11:20 修改

阅读量5k

点赞数 15

分类专栏：矩阵分析文章标签：算法机器学习人工智能

于 2024-10-23 14:35:26 首次发布

本文链接：https://blog.csdn.net/m0_53605808/article/details/143183467

版权

矩阵分析专栏收录该内容

35 篇文章

订阅专栏

1. 范数 (Norm)

定义：范数是定义在向量空间中的一种函数，用于测量向量的大小或长度。对于向量 x，范数表示为 ∥x∥。

性质：

非负性：∥x∥≥0，且 ∥x∥=0 当且仅当 x=0。
齐次性：∥αx∥=∣α∣∥x∥ 对任意标量 α成立。
三角不等式：∥x+y∥≤∥x∥+∥y∥。

分类：属于向量范数。

2. p 范数 (p-Norm)

定义：对于向量 $x = (x_1, x_2, \ldots, x_n)$ ，p 范数定义为：

$\|x\|_p = \left( \sum_{i=1}^{n} |x_i|^p \right)^{1/p}$

常用的 p 值包括 1、2 和 ∞。

性质：

p≥1：满足范数的所有性质。
p=1：曼哈顿范数（L1 范数），表示为 $\|x\|_1 = \sum |x_i|$ 。
p=2：欧几里得范数（L2 范数），表示为 $\|x\|_2 = \sqrt{\sum x_i^2}$ 。
p→∞：最大范数，表示为 $\|x\|_\infty = \max |x_i|$ 。

分类：属于向量范数。

3. 椭圆范数 (Elliptic Norm)

定义：椭圆范数是定义在向量空间中的一种范数，通常与椭圆体的几何性质相关。例如，在某些变换下形成椭圆形的单位球。

性质：

特定形式：通常表示为 $\|x\| = \sqrt{x^T A x}$ ，其中 A 是正定矩阵。
几何意义：椭圆范数的单位球在几何上表示为一个椭圆。

分类：属于向量范数。

4.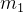 $m_1$ 范数 (Matrix 1-Norm)

定义：对于矩阵 A， $M_1$ 范数定义为矩阵所有的元素的绝对值之和：

$\|A\|_{m_1} = \sum_{i=1}^{m} \sum_{j=1}^{n} |a_{ij}|$

性质：

非负性： $\|A\|_{M_1} \geq 0$ 。
齐次性： $\|\alpha A\|_{M_1} = |\alpha| \|A\|_{M_1}$ 。
三角不等式： $\|A + B\|_{M_1} \leq \|A\|_{M_1} + \|B\|_{M_1}$ 。

分类：属于矩阵范数。

5. Frobenius 范数 (F-Norm)

定义：Frobenius 范数用于矩阵，定义为：

$\|A\|_F = \sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n} |a_{ij}|^2} = \sqrt{\text{tr}(A^* A)}$

其中 $a_{ij}$ 是矩阵 A 的元素，tr 表示迹（对角元素之和）。

性质：具有酉不变性。

分类：属于矩阵范数。

6. $m_\infty$ 范数 (Matrix Infinity-Norm)

定义：对于方阵 A， $m_\infty$ 范数无穷范数定义为各行元素绝对值之和的最大值：

$\|A\|_\infty = \max_{1\le i\le m} \sum_{j=1}^n |a_{ij}|.$

性质：

非负性和齐次性与范数相同。
满足三角不等式。
兼容性：与向量范数的性质类似，满足三角不等式。

分类：属于矩阵范数。

7. 矩阵 1 范数 (Matrix 1-Norm)

定义：矩阵 A 的 1 范数是所有列元素绝对值和的最大值：

$\|A\|_1 = \max_{1 \leq j \leq n} \sum_{i=1}^{m} |a_{ij}|$

这里 $a_{ij}$ 是矩阵 A 的元素。

性质：

非负性： $\|A\|_1 \geq 0$ 。
齐次性：对于标量 α ，有 $|\alpha A\|_1 = |\alpha| \|A\|_1$ 。
三角不等式： $\|A + B\|_1 \leq \|A\|_1 + \|B\|_1$ 。
与向量范数的关系：矩阵 1 范数等于对应的向量 1 范数的最大值。
矩阵 1 范数：最大列和，关注矩阵的列结构。

分类：属于矩阵范数。

8. 矩阵 2 范数 (Matrix 2-Norm)

定义：矩阵 A 的 2 范数（也称为谱范数）是其奇异值的最大值，或者可以通过以下方式定义：

$\|A\|_2 = \max_{\|x\|_2 = 1} \|Ax\|_2=max(\sigma_i )$

性质：

非负性： $\|A\|_2 \geq 0$ 。
齐次性：对于标量 α，有 $|\alpha A\|_2 = |\alpha| \|A\|_2$ 。
三角不等式： $\|A + B\|_2 \leq \|A\|_2 + \|B\|_2$ 。
酉不变性
等于最大的奇异值： $\|A\|_2$ 等于矩阵 A 的最大奇异值。
矩阵 2 范数：最大奇异值，关注矩阵对向量的拉伸效应。

分类：属于矩阵范数。

9. 矩阵无穷范数 (Matrix Infinity-Norm)

定义：矩阵 A 的无穷范数是所有行元素绝对值和的最大值：

$\|A\|_\infty = \max_{1 \leq i \leq m} \sum_{j=1}^{n} |a_{ij}|$

性质：

非负性： $\|A\|_\infty \geq 0$ 。
齐次性：对于标量 α，有 $\|\alpha A\|_\infty = |\alpha| \|A\|_\infty$ 。
三角不等式： $\|A + B\|_\infty \leq \|A\|_\infty + \|B\|_\infty$ 。
与向量范数的关系：矩阵无穷范数等于对应的向量无穷范数的最大值。
矩阵无穷范数：最大行和，关注矩阵的行结构。

分类：属于矩阵范数。

10. 矩阵M范数 (Max Norm)

定义：矩阵 A 的M范数是矩阵中绝对值最大的元素，定义为：

$\|A\|_{\text{M}} = \max({ m, n} )max|a_{ij}|$

性质：

非负性： $\|A\|_{\text{M}} \geq 0$ 。
齐次性：对于标量 α ，有 $\|\alpha A\|_{\text{M}} = |\alpha| \|A\|_{\text{M}}$ 。
三角不等式： $\|A + B\|_{\text{M}} \leq \|A\|_{\text{M}} + \|B\|_{\text{M}}$ 。

分类：属于矩阵范数。

11. 矩阵G范数 (Geometric Mean Norm)

定义：矩阵的几何平均范数是通过矩阵中元素的几何平均值来定义，通常定义为：

$\|A\|_{\text{G}} = \sqrt{mn}\max|a_{ij}|$

其中 $|a_{ij}|$ 是矩阵 A 的元素，m 是行数，n 是列数。

性质：

非负性： $\|A\|_{\text{G}} \geq 0$ ，且仅当所有元素为零时为零。
齐次性：对于标量 α，有 $\|\alpha A\|_{\text{G}} = |\alpha| \|A\|_{\text{G}}$ 。
三角不等式： $\|A + B\|_{\text{G}} \leq \|A\|_{\text{G}} + \|B\|_{\text{G}}$ 。

分类：属于矩阵范数。

区别：p 范数、椭圆范数、m1​ 范数、Frobenius 范数、 m∞ 范数、矩阵1范数、矩阵2范数、 矩阵∞ 范数、矩阵M范数、矩阵G范数

1. 范数 (Norm)

2. p 范数 (p-Norm)

3. 椭圆范数 (Elliptic Norm)

4. 范数 (Matrix 1-Norm)

5. Frobenius 范数 (F-Norm)

6. 范数 (Matrix Infinity-Norm)

7. 矩阵 1 范数 (Matrix 1-Norm)

8. 矩阵 2 范数 (Matrix 2-Norm)

9. 矩阵无穷范数 (Matrix Infinity-Norm)

10. 矩阵M范数 (Max Norm)

11. 矩阵G范数 (Geometric Mean Norm)

区别：p 范数、椭圆范数、m1 范数、Frobenius 范数、 m∞ 范数、矩阵1范数、矩阵2范数、矩阵∞ 范数、矩阵M范数、矩阵G范数

4. $m_1$ 范数 (Matrix 1-Norm)

6. $m_\infty$ 范数 (Matrix Infinity-Norm)