因变量为标量,自变量为向量
参考
y
y
y 为因变量,标量;
X
=
[
x
1
,
x
2
,
…
,
x
n
]
T
X=[x_1,x_2,\dots,x_n]^T
X=[x1,x2,…,xn]T 为自变量是向量,n维。
y
=
f
(
X
)
y=f(X)
y=f(X),即!!
y
=
f
(
x
1
,
x
2
,
…
,
x
n
)
y = f(x_1,x_2,\dots,x_n)
y=f(x1,x2,…,xn)
因此可以直接求导:
∂
y
∂
X
=
(
∂
y
∂
x
1
;
∂
y
∂
x
2
;
…
;
∂
y
∂
x
n
)
\frac{\partial y}{\partial X} = (\frac{\partial y}{\partial x_1};\frac{\partial y}{\partial x_2};\dots;\frac{\partial y}{\partial x_n})
∂X∂y=(∂x1∂y;∂x2∂y;…;∂xn∂y)
求导结果为n维向量
以
y
=
a
⃗
T
x
⃗
y = \vec a ^T\vec x
y=aTx:表示y为两个向量的内积,结果为一个标量
则求
∂
y
∂
x
⃗
\frac{\partial y}{\partial \vec x}
∂x∂y,只需求出所有的
∂
y
∂
x
⃗
i
\frac{\partial y}{\partial \vec x_i}
∂xi∂y即可。
具体方法为:
将
y
y
y的表达式展开成累加和的形式,然后套用标量的求导法则即可,这一方法适用于所有多维情况的求导。
解:
y
=
a
⃗
T
x
⃗
=
∑
i
=
1
n
a
i
x
i
y = \vec a^T\vec x=\sum_{i=1}^n a_i x_i
y=aTx=i=1∑naixi
故对
∀
i
\forall i
∀i:
∂
y
∂
x
i
=
a
i
\frac{\partial y}{\partial x_i} = a_i
∂xi∂y=ai
故:
∂
y
∂
x
⃗
=
(
∂
y
∂
x
1
;
∂
y
∂
x
2
;
…
;
∂
y
∂
x
n
)
=
(
a
1
;
a
2
;
…
;
a
n
)
=
a
\begin{aligned} \frac{\partial y}{\partial \vec x}&=(\frac{\partial y}{\partial x_1};\frac{\partial y}{\partial x_2};\dots;\frac{\partial y}{\partial x_n}) \\ ~&=(a_1;a_2;\dots ;a_n) \\ ~&=a \end{aligned}
∂x∂y =(∂x1∂y;∂x2∂y;…;∂xn∂y)=(a1;a2;…;an)=a
注意:若 y = x ⃗ 点乘 x ⃗ y=\vec x 点乘 \vec x y=x点乘x, 则求导结果是 2 x ⃗ 2\vec x 2x
例子:
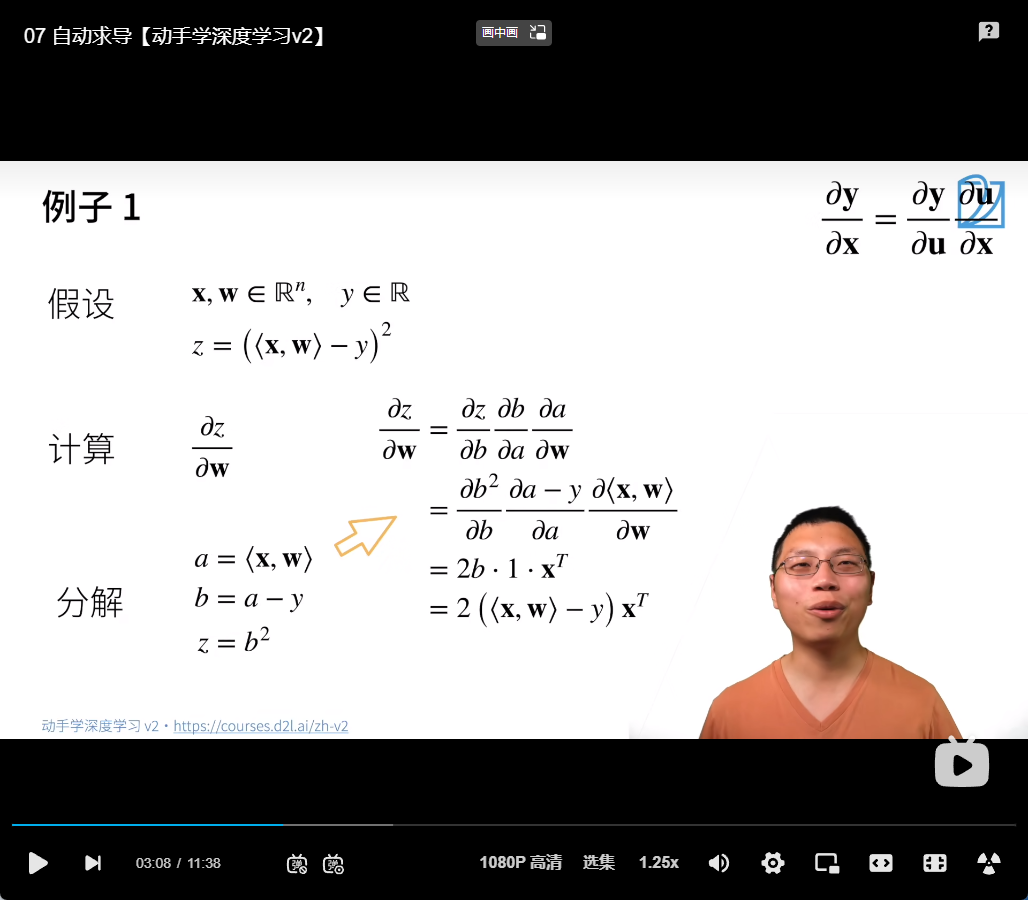
注意图中,向量
x
x
x与
w
w
w均写成了1n的形式,而不是我们通常的n1,因此最终算出来的结果里面为
x
T
x^T
xT,而不是
x
x
x
因变量、自变量均为向量
当自变量和因变量均为向量时,求导结果为一个矩阵,我们称该矩阵为雅可比矩阵(Jacobian Matrix)。

特别的,如果X为n*m的矩阵,w为m维向量,则
∂
X
∂
w
⃗
=
X
\frac{\partial X}{\partial \vec w} = X
∂w∂X=X
证明:
设
X
=
[
x
11
x
12
…
x
1
m
x
21
x
22
…
x
2
m
⋮
⋮
⋱
⋮
x
n
1
x
n
2
…
x
n
m
]
,
w
=
[
w
1
w
2
⋮
w
m
]
X = \begin{bmatrix} x_{11}&x_{12}&\dots&x_{1m}\\ x_{21}&x_{22}&\dots&x_{2m}\\ \vdots&\vdots&\ddots&\vdots\\ x_{n1}&x_{n2}&\dots&x_{nm} \end{bmatrix}, w = \begin{bmatrix} w_{1}\\ w_2\\ \vdots\\ w_m \end{bmatrix}
X=
x11x21⋮xn1x12x22⋮xn2……⋱…x1mx2m⋮xnm
,w=
w1w2⋮wm
则,
z
⃗
=
X
w
=
[
x
11
w
1
+
x
12
w
2
+
⋯
+
x
1
m
w
m
x
21
w
1
+
x
22
w
2
+
⋯
+
x
2
m
w
m
⋮
x
n
1
w
1
+
x
n
2
w
2
+
⋯
+
x
n
m
w
m
]
=
[
z
1
z
2
⋮
z
n
]
\vec z=Xw=\begin{bmatrix} x_{11}w_1+x_{12}w_2+\dots+x_{1m}w_m\\ x_{21}w_1+x_{22}w_2+\dots+x_{2m}w_m\\ \vdots\\ x_{n1}w_1+x_{n2}w_2+\dots+x_{nm}w_m \end{bmatrix}=\begin{bmatrix} z_1\\ z_2\\ \vdots\\ z_n \end{bmatrix}
z=Xw=
x11w1+x12w2+⋯+x1mwmx21w1+x22w2+⋯+x2mwm⋮xn1w1+xn2w2+⋯+xnmwm
=
z1z2⋮zn
则
∂
X
w
⃗
∂
w
⃗
=
∂
z
⃗
∂
w
⃗
=
[
∂
z
1
∂
w
1
∂
z
1
∂
w
2
…
∂
z
1
∂
w
m
∂
z
2
∂
w
1
∂
z
2
∂
w
2
…
∂
z
2
∂
w
m
⋮
⋮
⋱
⋮
∂
z
n
∂
w
1
∂
z
n
∂
w
2
…
∂
z
n
∂
w
m
]
=
[
x
11
x
12
…
x
1
m
x
21
x
22
…
x
2
m
⋮
⋮
⋱
⋮
x
n
1
x
n
2
…
x
n
m
]
=
X
\begin{aligned} \frac{\partial X\vec w}{\partial \vec w} &= \frac{\partial \vec z}{\partial \vec w}\\ &=\begin{bmatrix} \frac{\partial z_1}{\partial w_1}&\frac{\partial z_1}{\partial w_2}&\dots&\frac{\partial z_1}{\partial w_m}\\ \frac{\partial z_2}{\partial w_1}&\frac{\partial z_2}{\partial w_2}&\dots&\frac{\partial z_2}{\partial w_m}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial z_n}{\partial w_1}&\frac{\partial z_n}{\partial w_2}&\dots&\frac{\partial z_n}{\partial w_m}\\ \end{bmatrix}\\ &=\begin{bmatrix} x_{11}&x_{12}&\dots&x_{1m}\\ x_{21}&x_{22}&\dots&x_{2m}\\ \vdots&\vdots&\ddots&\vdots\\ x_{n1}&x_{n2}&\dots&x_{nm} \end{bmatrix}\\ &=X \end{aligned}
∂w∂Xw=∂w∂z=
∂w1∂z1∂w1∂z2⋮∂w1∂zn∂w2∂z1∂w2∂z2⋮∂w2∂zn……⋱…∂wm∂z1∂wm∂z2⋮∂wm∂zn
=
x11x21⋮xn1x12x22⋮xn2……⋱…x1mx2m⋮xnm
=X
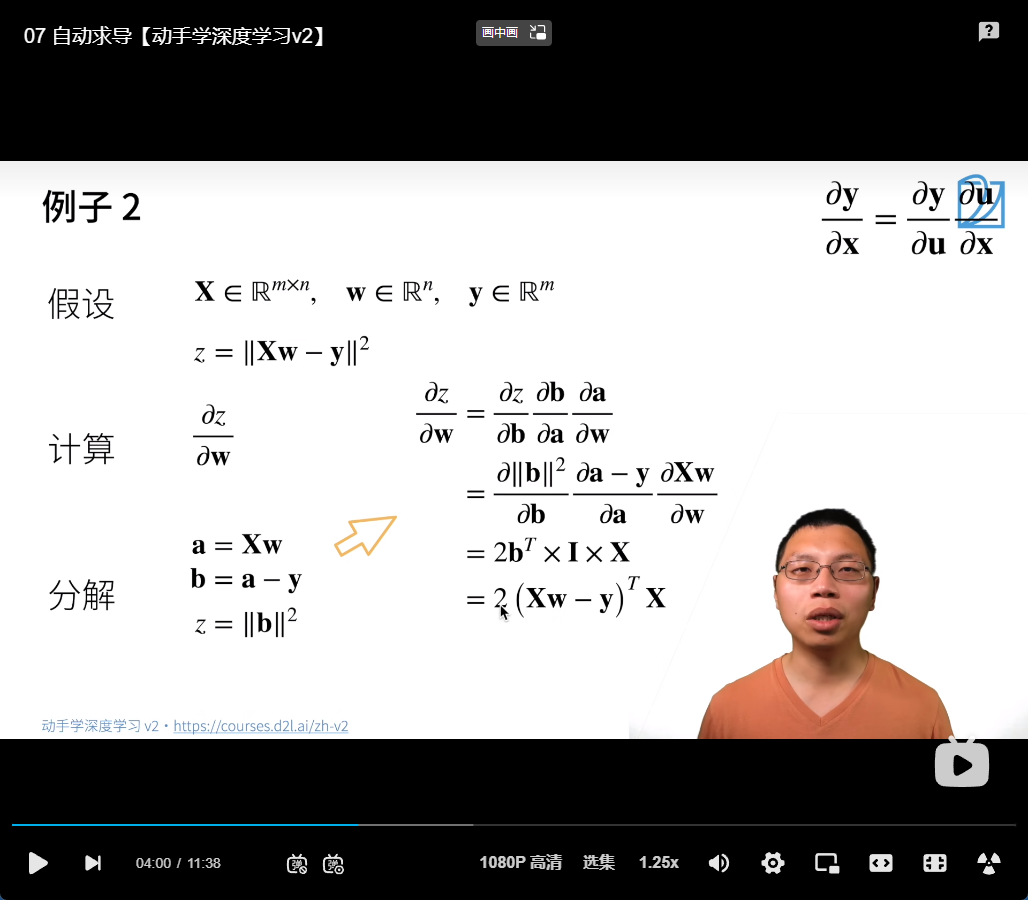
例子:























 8046
8046

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








