首先介绍什么是生成树。
生成树是相对于图的,假设图
G
=
(
V
G
,
E
G
)
G=(V_G,E_G)
G=(VG,EG),图
G
G
G 的生成树
T
=
(
V
T
,
E
T
)
T=(V_T,E_T)
T=(VT,ET) 是图
G
G
G 的子图,且满足
V
T
=
V
G
E
T
⊆
E
G
V_T=V_G\\ E_T\subseteq E_G
VT=VGET⊆EG
注意生成树的节点与图的节点相同,不是子集关系。
对于带权图来说,生成树的成本等于树所有边的权重之和,由此可以推出最小生成树的定义:
最小生成树:具有最小权重的生成树
下图就是连通图的一个最小生成树,注意最小生成树并不唯一
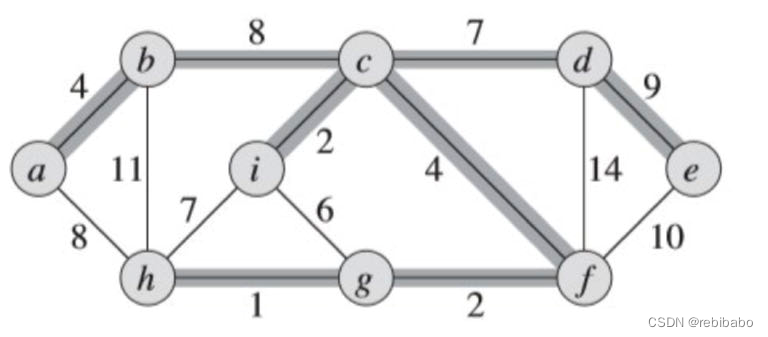
如何构造最小生成树
利用贪心的策略,每一个时刻都生长出最小生成树的一条边,并在整个循环过程中,边的集合 A A A 都要满足循环不变式:
在每遍循环前, A A A 是某棵最小生成树的一个子集。
处理策略:每一步,我们选择一条边 ( u , v ) (u,v) (u,v) 加入集合 A A A,使得 A A A 不违反循环不变式,则 A ∪ { ( u , v ) } A\ \cup\{(u,v)\} A ∪{(u,v)} 还是某棵最小生成树的子集,我们把这样的边叫做安全边。
我们可以得出最小生成树的基本生成算法:
G
E
N
E
R
I
C
−
M
S
T
(
G
,
ω
)
w
h
i
l
e
(
A
还
不
是
一
颗
最
小
生
成
树
)
找
到
一
条
安
全
边
(
u
,
v
)
A
=
A
∪
{
(
u
,
v
)
}
r
e
t
u
r
n
A
GENERIC-MST(G,\omega)\\\ \ \ while(A还不是一颗最小生成树)\\ \quad 找到一条安全边(u,v)\\ \quad A=A\ \cup\{(u,v)\}\\ return\ A\qquad\qquad\qquad\qquad
GENERIC−MST(G,ω) while(A还不是一颗最小生成树)找到一条安全边(u,v)A=A ∪{(u,v)}return A
那么如何判断一条边到底是不是最小生成树的一条边,即安全边呢?
一些定义
首先引入一些定义,最后我们可以得出寻找安全边的定理。
切割:无向图 G = ( V , E ) G=(V,E) G=(V,E) 的一个切割 ( S , V − S ) (S,V-S) (S,V−S) 是集合 V V V 的一个划分。
说白了就是将原来图的节点分成两半,下图的切割将图的节点划分成了
{
{
a
,
b
,
d
,
e
}
,
{
c
,
f
,
g
,
h
,
i
}
}
\{\{a,b,d,e\},\{c,f,g,h,i\}\}
{{a,b,d,e},{c,f,g,h,i}}。
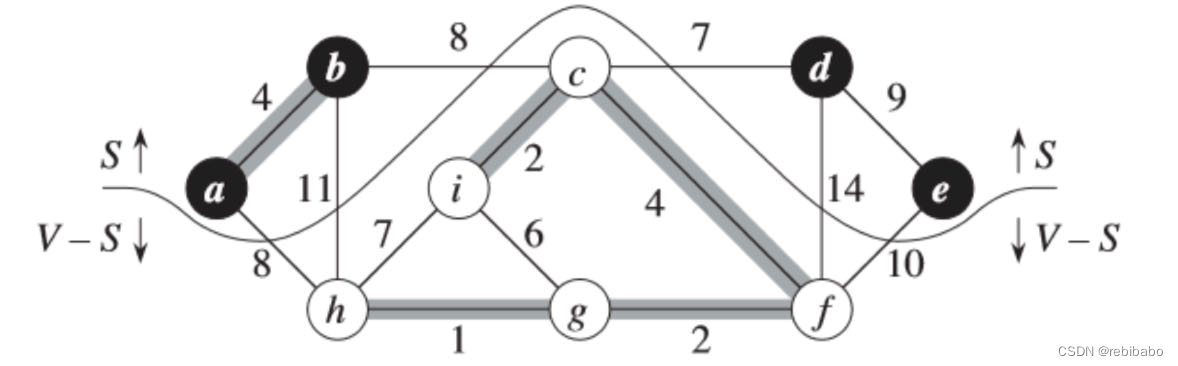
横跨切割:如果一条边
(
u
,
v
)
∈
E
(u,v)\in E
(u,v)∈E 的一个端点在集合
S
S
S 中,另一个端点在集合
V
−
S
V-S
V−S 中,则称该条边横跨切割
(
S
,
V
−
S
)
(S,V-S)
(S,V−S)。
尊重:如果边集 A A A 中不存在横跨某切割的边,则称该切割尊重集合 A A A。
轻量级边:在横跨一个切割的所有边中,权重最小的边称为轻量级边。
例如,在下面图中,存在横跨切割
(
S
,
V
−
S
)
(S,V-S)
(S,V−S) 的边有
(
b
,
c
)
,
(
c
,
d
)
,
(
b
,
h
)
,
(
d
,
f
)
,
(
a
,
h
)
,
(
e
,
f
)
(b,c),(c,d),(b,h),(d,f),(a,h),(e,f)
(b,c),(c,d),(b,h),(d,f),(a,h),(e,f)
而边为
(
c
,
d
)
(c,d)
(c,d) 是唯一一条轻量级边,因为其在所有横跨切割的边中的权重最小。
途中阴影边构成集合
A
A
A,其中不存在横跨该切割的边,所有切割
(
S
,
V
−
S
)
(S,V-S)
(S,V−S) 尊重集合
A
A
A。
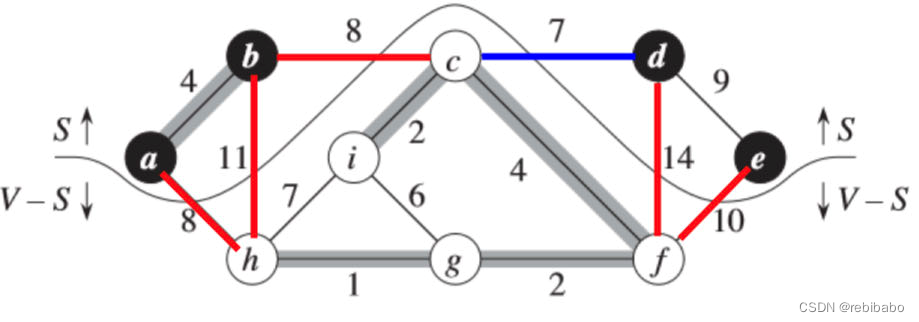
定理及其推论
定理:设 G = ( V , E ) G=(V,E) G=(V,E) 是一条有权无向图,设集合 A A A 为 E E E 的子集,且 A A A 包含于图 G G G 的某棵最小生成树中,设 ( S , V − S ) (S,V-S) (S,V−S) 是图 G G G 中尊重集合 A A A 的任意一个切割,又设 ( u , v ) (u,v) (u,v) 是横跨切割 ( S , V − S ) (S,V-S) (S,V−S) 的一条轻量级边,则边 ( u , v ) (u,v) (u,v) 对于集合 A A A 是安全的。
我们可以这样理解 G E N E R I C − M S T GENERIC-MST GENERIC−MST 算法,在算法推进过程中,集合 A A A 始终保持无环状态,且算法执行的任意时刻,图 G A G_A GA 是一个森林,其中的每一个连通分量都是一棵树。
而对于安全边 ( u , v ) (u,v) (u,v),由于 A ∪ { ( u , v ) } A\ \cup\{(u,v)\} A ∪{(u,v)} 必须无环,所以 ( u , v ) (u,v) (u,v) 必须连接的是森林 G A G_A GA 中的两个联通分量。
推论:设 G = ( V , E ) G=(V,E) G=(V,E) 是一个有权无向连通图,设集合 A A A 是 E E E 的一个子集,且 A A A 包含在图 G G G 的某棵最小生成树中。设 C = ( V C , E c ) C=(V_C,E_c) C=(VC,Ec) 为森林 G A = ( V , A ) G_A=(V,A) GA=(V,A) 中的一个连通分量,边 ( u , v ) ∈ E , ( u , v ) ∉ A (u,v)\in E,(u,v)\notin A (u,v)∈E,(u,v)∈/A,是 C C C 连接其他连通分量中权重最小的边,则边 ( u , v ) (u,v) (u,v) 对于集合 A A A 是安全的。
按照寻找安全边方法的不同,可分为Kruskal算法和Prim算法。
图的代码部分
我们用邻接表来存放边,其中节点下标为 1 − v e x N u m 1-vexNum 1−vexNum,边的下标用 c n t cnt cnt 来编号,每加入一条边, c n t cnt cnt 就加一,存放边的数组是 e d g e edge edge。
e d g e edge edge 存放了所有边,每一条边是结构体 n o d e node node, n e x nex next 表示该边在邻接表的下一条边的索引,相当于指针形式的 ∗ n e x t *next ∗next, t o to to 表示这条边指向的另一个节点标号, v v v 是边的权重。
h e a d [ i ] head[i] head[i] 存放的是节点 i i i 的第一条边在 e d g e edge edge 中的下标, v i s i t e d [ i ] visited[i] visited[i] 表示节点 i i i 是否遍历过, v e x N u m vexNum vexNum 为节点的个数。
class Graph{
int cnt,head[MAX],visited[MAX],vexNum; //用来给边命名,head[x]为节点x指向的第一条边 ,MAX为最大节点/边个数
struct node{
int next,to,v; //下一条边,该边指向的节点,边的长度
bool operator<(const node& n) const{return n.v<v;};
}edge[MAX],edge_copy[MAX];
图新加入一条有向边是用的 a d d add add 函数,加入无向边用 a d d 2 add2 add2。
void add(int x,int y,int v){ //添加有向边
cnt++; //边的命名cnt加一
edge[cnt].to=y; //该边指向节点为y
edge[cnt].v=v;
edge[cnt].next=head[x]; //在链表头插入新边
head[x]=cnt; //新边插入x的第一条边
}
void add2(int x,int y,int v){ //添加无向边
add(x,y,v);
add(y,x,v);
}
Kruskal算法
寻找安全边的方法:在所有连接森林中两棵不同树的边中,找权重最小的边 ( u , v ) (u,v) (u,v),依照的是上述的推论。
具体算法如下:
初始化森林,森林当中的每一颗树都是一个节点
将所有边按照权重按照从小到大的顺序排序
for 所有的边,依次取出权值最小的边(u,v)
if u和v不在同一个连通分量
then 将边(u,v)加入边集合A当中,并且连接u和v
return A
初始情况 A = ∅ A=\varnothing A=∅, G A G_A GA是一个森林,该森林的每一棵树都是图中的一个节点。
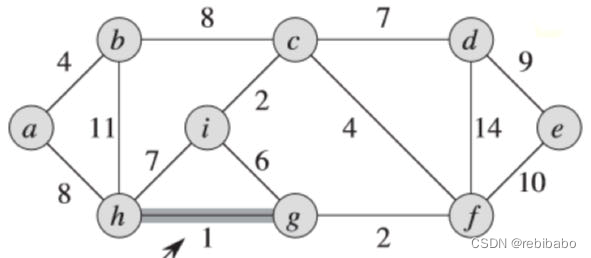
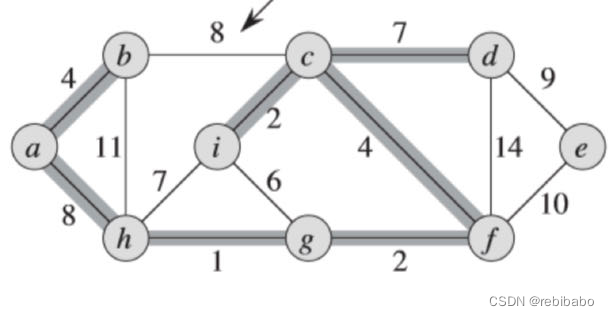
我们拿下面的图来举例,权重最小的边是
(
h
,
g
)
(h,g)
(h,g),我们把它加入到
A
A
A 中,图中用粗灰线表示。
我们再选取最小权重的边
(
i
,
c
)
(i,c)
(i,c),把它加入到
A
A
A 中。
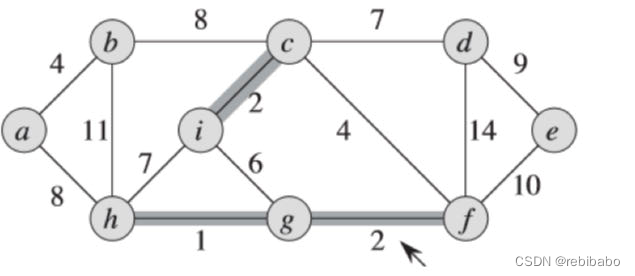
下面依次展示了该算法的全过程
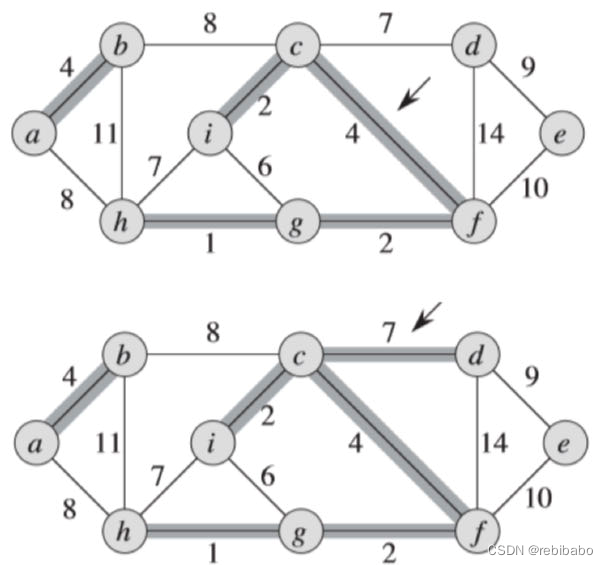
因为添加完
(
b
,
c
)
(b,c)
(b,c) 以后会成环
a
,
b
,
c
,
g
,
h
a,b,c,g,h
a,b,c,g,h,所以不将边
(
b
,
c
)
(b,c)
(b,c) 加入
A
A
A 中。
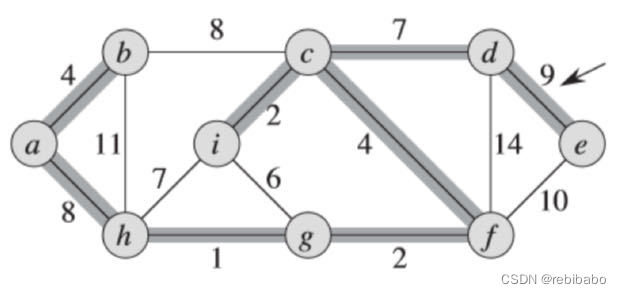
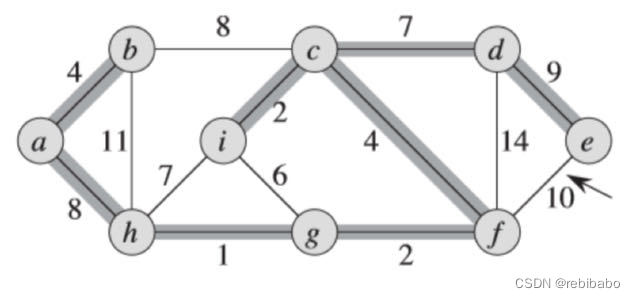
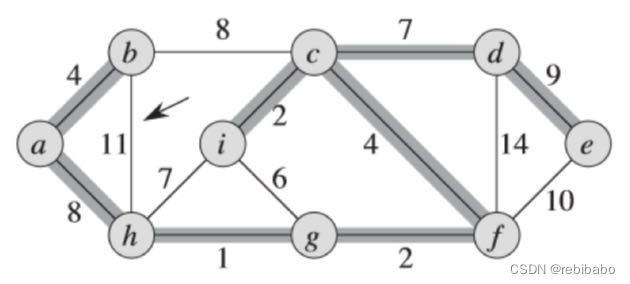
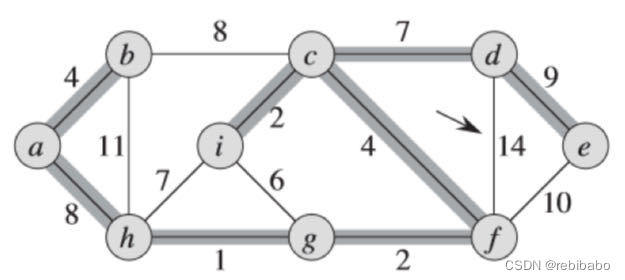
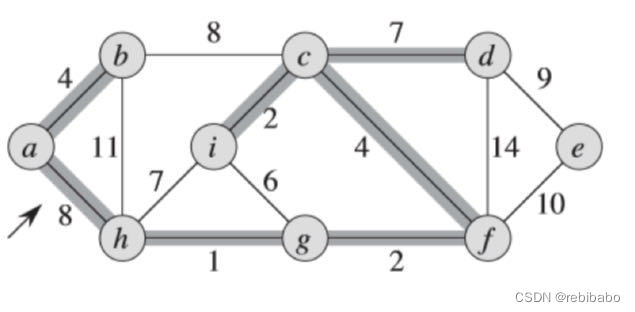
遍历完所有边以后,我们得到了最小生成树,权重之和为37。
我们首先将所有边按照权重排序,时间复杂度为 O ( E l o g E ) O(ElogE) O(ElogE),我们使用并查集的方式来表示森林,如果不知道并查集的小伙伴可以看我的另一篇博客,(199条消息) 并查集C++实现——算法设计与分析,含代码解释_rebibabo的博客-CSDN博客,我们依次取出排好序的边,如果边连接两个连通分量,则我们将这两个联通分量相连,否则我们跳过,不然就会形成环了,我们一共要遍历 ∣ E ∣ |E| ∣E∣ 次,每一次我们都合并了两个森林,时间复杂度参考并查集的union操作,是 O ( l o g E ) O(logE) O(logE) 的,所以循环的时间复杂度也是 O ( E l o g E ) O(ElogE) O(ElogE)。
考虑到 ∣ E ∣ < ∣ V ∣ 2 |E|<|V|^2 ∣E∣<∣V∣2,则有 l o g ∣ E ∣ = O ( l o g ∣ V ∣ ) log|E|=O(log|V|) log∣E∣=O(log∣V∣),所以Kruskal算法的时间复杂度可以表示为 O ( E l o g V ) O(ElogV) O(ElogV)。
并查集的代码部分
合并两个联通图的操作是connect,判断是否属于同一个连通图使用isConnected。
class UnionFind {
int id[MAX]; //
int contain[MAX]; // 包含多少节点
int minIndex; // 范围
int maxIndex; // 范围
int cnt; //连通分量的个数
public :
UnionFind() {}
UnionFind(int minIndex, int maxIndex) {
this->minIndex = minIndex;
this->maxIndex = maxIndex;
this->cnt = maxIndex - minIndex + 1; // 连通分量的个数
for (int i = minIndex; i <= maxIndex ; i++) {
id[i] = i;
contain[i] = 1;
}
}
int getRoot(int p) {//采用递归的方式
if (id[p] == p) { //自己就是根节点
return p;
}
else {
int d = id[p];
int root = getRoot(d);
if (d != root) {
id[p] = root; //将当前节点的id设置成根节点
contain[d] -= contain[p]; //因为d的子树移到了根节点,所以要将d的contain减去p的contain
}
return root;
}
}
bool isConnected(int p, int q) {
return getRoot(q) == getRoot(p);
}
bool connect(int p, int q) {
int pRoot = getRoot(p);
int qRoot = getRoot(q);
if (qRoot == pRoot) {
return false; // 已经在同一个set里面了,已经在同一个连通分量里面了
}
else {
if(contain[p] >= contain[q]) {
id[qRoot] = pRoot;
contain[pRoot] += contain[qRoot];
}
else {
id[pRoot] = qRoot;
contain[qRoot] += contain[pRoot];
}
}
cnt --; //连通分量少1
}
};
Kruscal代码
首先将所有边按照权重排序,排序会打乱边的顺序,所以拷贝一份放在 e d g e _ c o p y edge\_copy edge_copy 里再将排好序的边表示为 ( l , r , v ) (l,r,v) (l,r,v),放在 v e c t o r e vector\ e vector e 中, 然后建立森林 u f uf uf,每一个连通分量为一个节点,然后依次遍历排好序的边集合 e e e,每次从中选取权值最小的边,如果这条边的两端 l , r l,r l,r 横跨两个连通分量,即 u f . i s C o n n e c t ( ) uf.isConnect() uf.isConnect() 为 f a l s e false false ,则将这两节点所在的联通分量连起来,执行 u f . c o n n e c t uf.connect uf.connect 操作,如果这条边不横跨两个连通分量,则跳过,依次循环 ∣ E ∣ |E| ∣E∣ 遍,具体代码和注释如下:
int Kruskal(){
cout<<"最小生成树:";
int sum=0;
memcpy(edge_copy,edge,sizeof(edge)); //拷贝边edge一份,排序会打乱原来边的顺序
sort(edge_copy,edge_copy+MAX); //将边按照权重排序
vector<vector<int> >edges; //将edge改成所有边的集合(l,r,v),表示左节点,右节点和权重
for(int i=0;i<MAX&&edge_copy[i].v;i+=2){ //按照边的长度从大到小排序,遇到0则结束
vector<int> e;
//sort函数不会改变原来的顺序,所以连续两个相同大小的边的两个to节点组成一条的两端节点
e.push_back(edge_copy[i].to), e.push_back(edge_copy[i+1].to), e.push_back(edge_copy[i].v);
edges.insert(edges.begin(),e);//逆序插入
}
UnionFind uf(1,MAX); //构建所有节点为单独一棵树的森林
for(int i=0;i<edges.size();i++){ //遍历所有边
if(!uf.isConnected(edges[i][0],edges[i][1])){ //如果这两棵树不相通
uf.connect(edges[i][0],edges[i][1]);//则连接这两个树,且连接两棵树的该边是一条安全边,即权重最小且不会形成环
sum+=edges[i][2]; //计算权重和
printf("(%d,%d,%d)",edges[i][0],edges[i][1],edges[i][2]);
}
}
cout<<endl<<"最小生成树路径之和为:"<<sum<<endl;
memset(visited,0,sizeof(visited));
return sum;
}
Prims算法
简单来说,Prim算法每一步都在连接集合 A A A 和 A A A 之外所有节点的边当中,权重最小的边,参考了上面的定理,具体算法如下
任意选择一个节点a开始,将a的所有邻边放在待选边集合E当中
while E不为空
u是E中权值最小的边对应的另一个节点
for u的所有邻边(u,v)
if v没有访问过
then 将(u,v)加入E中
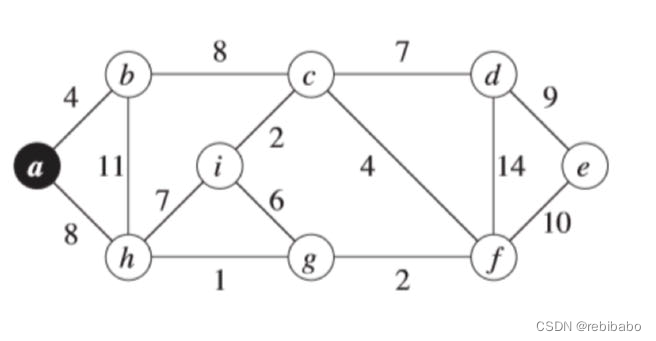
就拿下图打比方,假设一开始的节点为
a
a
a,我们选择与
a
a
a 相邻的所有边当中权值最小的边
(
a
,
b
)
(a,b)
(a,b),将
b
b
b 标记为访问过。
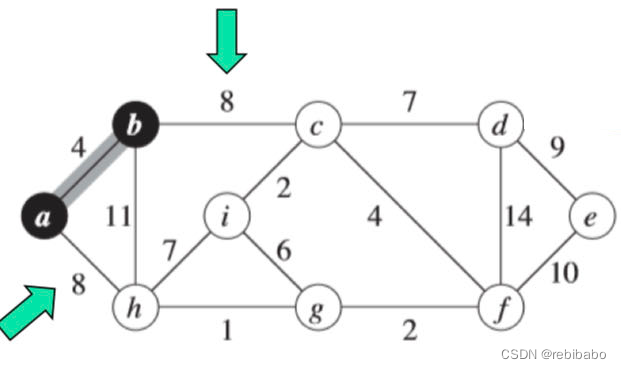
接着,我们从和
a
,
b
a,b
a,b 相邻的所有边当中选取一个最短的边,
(
b
,
c
)
(b,c)
(b,c) 或者
(
a
,
h
)
(a,h)
(a,h) 都可以,我们暂且选取
(
b
,
c
)
(b,c)
(b,c)。
接着我们选择和
a
,
b
,
c
a,b,c
a,b,c 相邻的所有边当中权重最小的,选择
(
c
,
i
)
(c,i)
(c,i),依次类推,如果这条边的另一端的节点访问过,则选择次大的边。
如果我们考虑使用优先队列的话,能够使得每一次查找相邻权值最短边的时间缩短为 O ( l o g V ) O(logV) O(logV),而一共要遍历节点 ∣ V ∣ |V| ∣V∣ 次,所以Prim的时间复杂度为 O ( V l o g V ) O(VlogV) O(VlogV)
下面是Prim算法的代码
int Prim(int v0) {
int sum=0, cur_node=v0;
priority_queue<node> q;
visited[v0]=1; //设置visited
for(int i=head[v0];i;i=edge[i].next){ //先将v0的所有邻边入队
q.push(edge[i]);
}
while(!q.empty()){
node n=q.top();
q.pop();
if(visited[n.to]==0){ //该边是cur_node相邻边中权重最小的边,且还没有遍历过下一节点
cur_node=n.to; //设置当前遍历到的节点,方便打印最小生成树
visited[n.to]=1; //设置visited
sum+=n.v;
for(int i=head[n.to];i;i=edge[i].next){
q.push(edge[i]); //把当前节点的所有邻边入队
}
}
}
cout<<sum<<endl;
memset(visited,0,sizeof(visited));
return sum;
}
完整代码
#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
#define MAX 1000
struct vertex{
int node;
int dis;
bool operator<(const vertex &n) const {return n.node<node;};
};
class UnionFind {
int id[MAX]; //
int contain[MAX]; // 包含多少节点
int minIndex; // 范围
int maxIndex; // 范围
int cnt; //连通分量的个数
public :
UnionFind() {}
UnionFind(int minIndex, int maxIndex) {
this->minIndex = minIndex;
this->maxIndex = maxIndex;
this->cnt = maxIndex - minIndex + 1; // 连通分量的个数
for (int i = minIndex; i <= maxIndex ; i++) {
id[i] = i;
contain[i] = 1;
}
}
int getRoot(int p) {//采用递归的方式
if (id[p] == p) { //自己就是根节点
return p;
}
else {
int d = id[p];
int root = getRoot(d);
if (d != root) {
id[p] = root; //将当前节点的id设置成根节点
contain[d] -= contain[p]; //因为d的子树移到了根节点,所以要将d的contain减去p的contain
}
return root;
}
}
bool isConnected(int p, int q) {
return getRoot(q) == getRoot(p);
}
bool connect(int p, int q) {
int pRoot = getRoot(p);
int qRoot = getRoot(q);
if (qRoot == pRoot) {
return false; // 已经在同一个set里面了,已经在同一个连通分量里面了
}
else {
if(contain[p] >= contain[q]) {
id[qRoot] = pRoot;
contain[pRoot] += contain[qRoot];
}
else {
id[pRoot] = qRoot;
contain[qRoot] += contain[pRoot];
}
}
cnt --; //连通分量少1
}
};
class Graph{
int cnt,head[MAX],visited[MAX],vexNum; //用来给边命名,head[x]为节点x指向的第一条边 ,MAX为最大节点/边个数
struct node{
int next,to,v; //下一条边,该边指向的节点,边的长度
bool operator<(const node& n) const{return n.v<v;};
}edge[MAX],edge_copy[MAX];
public:
Graph(int num){
cnt=0;
vexNum=num;
memset(head,0,sizeof(head));
memset(visited,0,sizeof(visited));
memset(edge,0,sizeof(edge));
}
void add(int x,int y,int v){ //添加有向边
cnt++; //边的命名cnt加一
edge[cnt].to=y; //该边指向节点为y
edge[cnt].v=v;
edge[cnt].next=head[x]; //在链表头插入新边
head[x]=cnt; //新边插入x的第一条边
}
void add2(int x,int y,int v){ //添加无向边
add(x,y,v);
add(y,x,v);
}
void show(){
for(int i=0;i<MAX;i++){ //遍历各节点
for(int j=head[i];j;j=edge[j].next){ //如果j等于0,说明没有边了
printf("(%d,%d,%d)",i,edge[j].to,edge[j].v);
}
if(head[i])
cout<<endl;
}
}
int Prim(int v0) {
int sum=0, cur_node=v0;
priority_queue<node> q;
visited[v0]=1; //设置visited
for(int i=head[v0];i;i=edge[i].next){ //先将v0的所有邻边入队
q.push(edge[i]);
}
while(!q.empty()){
node n=q.top();
q.pop();
if(visited[n.to]==0){ //该边是cur_node相邻边中权重最小的边,且还没有遍历过下一节点
cur_node=n.to; //设置当前遍历到的节点,方便打印最小生成树
visited[n.to]=1; //设置visited
sum+=n.v;
for(int i=head[n.to];i;i=edge[i].next){
q.push(edge[i]); //把当前节点的所有邻边入队
}
}
}
cout<<sum<<endl;
memset(visited,0,sizeof(visited));
return sum;
}
int Kruskal(){
cout<<"最小生成树:";
int sum=0;
memcpy(edge_copy,edge,sizeof(edge));
sort(edge_copy,edge_copy+MAX);
vector<vector<int> >edges; //将edge改成所有边的集合(l,r,v)
for(int i=0;i<MAX&&edge_copy[i].v;i+=2){ //按照边的长度从大到小排序,遇到0则结束
vector<int> e;
//sort函数不会改变原来的顺序,所以连续两个相同大小的边的两个to节点组成一条的两端节点
e.push_back(edge_copy[i].to), e.push_back(edge_copy[i+1].to), e.push_back(edge_copy[i].v);
edges.insert(edges.begin(),e);//逆序插入
}
UnionFind uf(1,MAX); //构建所有节点为单独一棵树的森林
for(int i=0;i<edges.size();i++){ //遍历所有边
if(!uf.isConnected(edges[i][0],edges[i][1])){ //如果这两棵树不相通
//则连接这两个树,且连接两棵树的该边是一条安全边,即权重最小且不会形成环
uf.connect(edges[i][0],edges[i][1]);
sum+=edges[i][2];
printf("(%d,%d,%d)",edges[i][0],edges[i][1],edges[i][2]);
}
}
cout<<endl<<"最小生成树路径之和为:"<<sum<<endl;
memset(visited,0,sizeof(visited));
return sum;
}
};
int main(void){
Graph g(6);
int temp[9][3]={{1,6,14},{1,2,7},{1,3,9},{3,6,2},{2,3,10},{2,4,15},{3,4,11},{5,6,9},{4,5,6}};
for(int i=0;i<9;i++)
g.add2(temp[i][0],temp[i][1],temp[i][2]);
g.show();
g.Prim(1);
g.Kruskal();
}























 1356
1356











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










