DDA数值微分法详解

Curz酥

已于 2022-09-13 23:00:58 修改

阅读量5.9k

点赞数 5

分类专栏：计算机图形学文章标签： c++ 算法 c语言图像处理图形渲染

于 2022-09-13 22:59:39 首次发布

本文链接：https://blog.csdn.net/m0_56494923/article/details/126842774

版权

计算机图形学专栏收录该内容

12 篇文章

订阅专栏

DDA算法，是根据直线的微分方程来计算△x和△y 生成直线的扫描转换算法。

下面给出一道例题，来讲解下DDA算法的计算步骤：

题目如下

解：我们按照题意画好了直线：

接下来就是使用DDA算法生成像素了

首先需要得到直线的斜率m，计算方法是利用直线方程中的点斜式 $y-y1=m(x-x1)$ 变形

成 $m=\frac{y1-y0}{x1-x0}=\frac{\Delta y}{\Delta x}$ 计算得到。

接着从x的左端点x1开始，向右端点x2步进，步长为一个像素，计算相应的y坐标y=mx+b；取像素点 (x, round(y)) 作为当前点的坐标(round表示四舍五入)，即：当x每递增1，y递增m(即直线斜率)：

提示：刚开始x=0，y=0.5，然后x增加1，y增加0.4(斜率)，···以此类推

这样，依次得到了坐标(0,0) (1,0) (2,1) (3,1) (4,2) (5,2)。

对坐标处添加像素，可得如下图像：

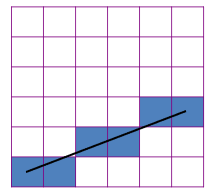
至此，通过DDA算法确定一组最佳逼近目标直线的像素已经完成。

注意本题的算法仅适用于|m| ≤1的情形。在这种情况下，x每增加1, y最多增加1。当 |m| >1时，必须把x，y地位互换，否则会导致画出来的像素点之间跳跃幅度过大。互换即y=mx+b变成x=(1/m)(y-b)，即y增加1，x增加1/m。

DDA算法伪代码(C语言)：

void DDALine(int x1,int y1,int x2,int y2,int color){
    int x；							
	float dx, dy, y, m;					
	dx = x2-x1, dy=y2-y1;					   
	m=dy/dx, y=y1;	 					   
	for (x=x1; x<=x2； x++)					   
	{  SetPixel (x, int(y+0.5), color);		   
	   y=y+m;
    }
}

DDA算法的优缺点：