方差分析、T检验、卡方分析｜LSD检验可用于方差同质性检验｜LSD检验法与t检验相比的优点

alwaysuzybai

已于 2022-11-07 14:56:10 修改

阅读量7.4k

点赞数 5

分类专栏：数学建模文章标签： python 开发语言

于 2022-11-07 10:37:56 首次发布

本文链接：https://blog.csdn.net/m0_57656758/article/details/127724781

版权

数学建模专栏收录该内容

27 篇文章 10 订阅

订阅专栏

1.概况

差异研究的目的在于比较两组数据或多组数据之间的差异，通常包括以下几类分析方法，分别是方差分析、T检验和卡方检验。

X数据类型	X组别	Y数据类型	分析方法
定类	2组或多组	定量	方差
定类	仅2组	定量	T检验
定类	2组或多组	定类	卡方

核心区别在于：数据类型不同，如果是定类和定类之间，此时应该使用卡方分析，如果是定类和定量之间，此时应该使用方差分析或者T检验。

而方差分析和T检验的区别在于，对于T检验的X来讲，其只能为2个类别比如男和女。如果X为3个类别比如本科以下，本科，本科以上；此时只能使用方差分析。

在这里插入图片描述

2.方差分析

根据X的不同，方差分析又可以进行细分。X的个数为一个时，我们称之为单因素方差；X为2个时则为双因素方差；X为3个时则称作三因素方差，依次下去。当X超过1个时，统称为多因素方差。

2.1单因素

单因素方差分析,用于分析定类数据与定量数据之间的关系情况。在使用单因素方差分析时，需要每个选项的样本量大于30，比如男性和女性样本量分别是100和120，如果出现某个选项样本量过少时应该首先进行组别合并处理，比如研究不同年龄组样本对于研究变量的差异性态度时，年龄小于20岁的样本量仅为20个，那么需要将小于20岁的选项与另外一组(比如20~25岁)的组别合并为一组，然后再进行单因素方差分析。

如果选项无法进行合并处理，比如研究不同专业样本对于变量的态度差异，研究样本的专业共分为市场营销、心理学、教育学和管理学四个专业，这四个专业之间为彼此独立无法进行合并组别，但是市场营销专业样本量仅为20并没有代表意义，因此可以考虑首先筛选出市场营销专业，即仅比较心理学，教育学和管理学这三个专业对某变量的差异性态度，当对比的组别超过三个，并且呈现出显著性差异时，可以考虑使用事后检验进一步对比具体两两组别间的差异情况。

2.2双因素

双因素方差分析,用于分析定类数据(2个)与定量数据之间的关系情况，例如研究人员性别,学历对于网购满意度的差异性;以及男性或者女性时,不同学历是否有着网购满意度差异性;或者同一学历时,不同性别是否有着网购满意度差异性。

2.3多因素

多因素方差分析通常用于类实验式问卷研究。在方法选择上，问卷研究通常会使用方差分析，但某些专业，比如心理学、教育学或者师范类专业等涉及到实验研究时，更多会使用T检验进行分析，另外方差分析与T检验还有较多差异，在某些分析中只能使用其中一种。

3.T检验

T检验共分为三种方法，分别是独立样本T检验，配对样本T检验和单样本T检验。

3.1独立样本T检验

独立样本T检验和单因素方差分析功能上基本一致，但是独立样本T检验只能比较两组选项的差异，比如男性和女性。相对来讲，独立样本T检验在实验比较时使用频率更高，尤其是生物、医学相关领域。针对问卷研究，如果比较的类别为两组，独立样本T检验和单因素方差分析均可实现，研究者自行选择使用即可。

3.2配对样本T检验

独立样本T检验和配对样本T检验功能上都是比较差异，而且均是比较两个组别差异。但二者有着实质性区别，如果是比较不同性别，婚姻状况(已婚和未婚)样本对某变量的差异时，应该使用独立样本T检验。如果比较组别之间有配对关系时，只能使用配对样本T检验，配对关系是指类似实验组和对照组的这类关系。另外独立样本T检验两组样本个数可以不相等，而配对样本T检验的两组样本量需要完全相等，并且独立样本T检验与配对样本T检验时在SPSS的数据放置格式不同。

3.3单样本T检验

T检验的第三种分析方法为单样本T检验。比如问卷某题项选项表示为1分代表非常不满意，2分代表比较不满意，3分代表一般，4分代表比较满意，5分代表非常满意，当分析样本对此题项的态度是否有明显的倾向，比如明显高于3分或者明显低于3分时，即可以使用单样本T检验。单样本T检验是比较某个题项的平均得分是否与某数字(例子是与3进行对比)有着明显的差异，如果呈现出显著性差异，即说明明显该题项平均打分明显不等于3分。此分析方法在问卷研究中较少使用，平均得分是否明显不为3分可以很直观的看出，而不需要单独进行检验分析。三种T检验均可在SPSS分析方法中找到并使用。

4.卡方分析

卡方检验用于分析定类数据与定类数据之间的关系情况。例如研究人员想知道两组学生对于手机品牌的偏好差异情况，则应该使用卡方分析。卡方是通过分析不同类别数据的相对选择频数和占比情况，进而进行差异判断，单选题或多选题均可以使用卡方分析进行对比差异分析。

5.LSD法

LSD为最小显著差异(least significant difference)t检验,适用于某一对或几对在专业上有非凡价值的均数间差别的比较。提供p值。由Fisher最先提出，本质上是一种t检验。通常用于1对或者几对专业上有特殊意义的样本均数间的比较。

为了更好的理解LSD法的计算原理，我们首先回顾两独立样本T检验：

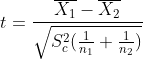
$t=\frac{\overline{X_{1}}-\overline{X_{2}}}{\sqrt{S_{c}^{2}(\frac{1}{n_{1}}+\frac{1}{n_{2}})}}$

其中 $S_{c}^{2}$ 是两个样本的联合估计的方差 (满足样本方差齐次性的前提下)，本质就是组内误差的均方，该统计量服从自由度为 $N-2$ 的 $t$ 分布。

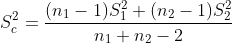
$S_{c}^{2}=\frac{(n_{1}-1)S_{1}^{2}+(n_{2}-1)S_{2}^{2}}{n_{1}+n_{2}-2}$

与上述类似，LSD法也进行的是两两比较的t检验。所不同的是，在满足方差齐性的前提下，LSD法采用所有样本的联合方差来估计均数差的标准误，而不是要比较的两个样本的联合方差。以三样本之间均数差异比较为例，其公式为：

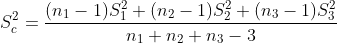
$S_{c}^{2}=\frac{(n_{1}-1)S_{1}^{2}+(n_{2}-1)S_{2}^{2}+(n_{3}-1)S_{3}^{2}}{n_{1}+n_{2}+n_{3}-3}$

LSD法往往计算最小显著差异，即：

$LSD=t_{\alpha /2}\sqrt{S_{c}^{2}(\frac{1}{n_{1}}+\frac{1}{n_{2}})}$

当两组均数差大于LSD时，说明差异达到显著的水平，也就可以拒绝零假设，认为两组均数不相等。需要注意的是，LSD法单次比较的检验水准仍然为 $\alpha$ 。LSD法检验的灵敏度最高，但是会因为对比的频数增加使得第一类型错误概率增加。为解决该问题，便出现了Sidak法和Bonferroni法。

6.SNK法

SNK法全称Newman-Keuls或者Student-Newman-Keuls，为student-newman-keuls三人姓氏的缩写，检验统计量为q，亦称q检验，适用于多个均数的两两比较，常用于探索性研究。只告诉有无差异，不提供精确p值。

7.LSD法优点

似乎是LSD法得出的p值稍小，在p值接近0.05的时候，比较轻易得出有统计学差异，而SNK方法得出的p值比较保守，相对不易得出p小于0.05。因而SNK法又不及LSD法灵敏。

8.检验方差同质性

当使用线性模型进行数据分析后，应该检测其残差方差是否同质。

常见检测方法

两个变量：F-test；

多个变量： Bartlet's test, Levene's test ( modified后则成为Brown-Forsythe test）,Breusch-Pagan Test， Filigner-Killen's test；

对于随后的所有这些检验，零假设是所有总体方差均相等，替代假设是其中至少有两个不同。因此，小于0.05的p值表明方差显着不同，并且违反了方差假设的同质性；

最常用的检测算法为Levene's test，因为它对偏离正态性不敏感。

文章参考

7.6 - Tests for Constant Error Variance | STAT 501

统计推断——假设检验——方差分析之多重比较（LSD法、Sidak法、Bonferroni法、Dunnett法、Tukey法、SNK 法、Duncan法）_xia ge tou lia的博客-CSDN博客_lsd法

alwaysuzybai

关注

5
点赞
踩
34

收藏

觉得还不错? 一键收藏
0
评论
方差分析、T检验、卡方分析｜LSD检验可用于方差同质性检验｜LSD检验法与t检验相比的优点

如果选项无法进行合并处理，比如研究不同专业样本对于变量的态度差异，研究样本的专业共分为市场营销、心理学、教育学和管理学四个专业，这四个专业之间为彼此独立无法进行合并组别，但是市场营销专业样本量仅为20并没有代表意义，因此可以考虑首先筛选出市场营销专业，即仅比较心理学，教育学和管理学这三个专业对某变量的差异性态度，当对比的组别超过三个，并且呈现出显著性差异时，可以考虑使用事后检验进一步对比具体两两组别间的差异情况。而方差分析和T检验的区别在于，对于T检验的X来讲，其只能为2个类别比如男和女。
复制链接

扫一扫