目录
一、高维数据映射为低维数据
在之前学习的过程中,我们得知降维就是将一个样本和一个轴w进行点乘的结果,即该样本映射到这个轴上得到的那个大小。如果我们将样本1去乘以W1,W2,W3...Wk,这样我就得到了一个数不同的向量,即样本1映射到了Wk这个坐标系上,然后得到的一个新的k维向量。由于k小于n,因此我们完成了一个样本从n维向k维的映射,以此类推,就将所有的样本从n维映射到了k维。

代码示例:
#封装自定义的PCA类
import numpy as np
class PCA:
def __init__(self,n_components):
# 初始化PCA
assert n_components >= 1,"n_components must be valid"
self.n_components = n_components
self.components_ = None
def fit(self,X,eta=0.01,n_iters=1e4):
# 获取数据集X的前n个主成分
assert self.n_components <= X.shape[1],\
"n_components must not be greater than the feature number of X"
# 均值归0
def demean(X):
return X - np.mean(X, axis=0)
# 设置目标函数
def f(w, X):
return np.sum((X.dot(w) ** 2)) / len(X)
# 数学推导函数
def df(w, X):
return X.T.dot(X.dot(w)) * 2. / len(X)
# 使w始终保持为单位向量
def direction(w):
return w / np.linalg.norm(w)
# 第一主成分——梯度上升法
def first_component(X, initial_w, eta, n_iters=1e4, epsilon=1e-8):
w = direction(initial_w)
i_iter = 0
while i_iter < n_iters:
gradient = df(w, X)
last_w = w
w = w + eta * gradient
w = direction(w)
if (abs(f(w, X) - f(last_w, X)) < epsilon):
break
i_iter += 1
return w
X_pca = demean(X)
self.components_ = np.empty(shape=(self.n_components,X.shape[1]))
for i in range(self.n_components):
initial_w = np.random.random(X_pca.shape[1])
w = first_component(X_pca,initial_w,eta,n_iters)
self.components_[i,:] = w
X_pca = X_pca - X_pca.dot(w).reshape(-1,1) * w
return self
# 从高维映射到低维
def transform(self,X):
# 将给定的X,映射到各个主成分分量中
assert X.shape[1] == self.components_.shape[1]
return X.dot(self.components_.T)
# 从低维映射到高维
def inverse_transform(self,X):
# 将给定的X,反向映射回原来的特征空间
assert X.shape[1] == self.components_.shape[0]
return X.dot(self.components_)
# 打印结果
def __repr__(self):
return "PCA(n_components=%d)" % self.n_components
测试:
import numpy as np
import matplotlib.pyplot as plt
#生成虚拟测试用例
X = np.empty((100,2))
X[:,0] = np.random.uniform(0.,100.,size=100)
X[:,1] = 0.75 * X[:,0] + 3.+ np.random.normal(0,10.,size=100)
from mySklearn.PCA import PCA
pca = PCA(n_components=1) #生成一个主成分
pca.fit(X)
X_reduction = pca.transform(X) #从二维降维成一维
X_restore = pca.inverse_transform(X_reduction) #再从一维恢复成二维
#绘制图形展示
plt.scatter(X[:,0],X[:,1],color='b',alpha=0.5)
plt.scatter(X_restore[:,0],X_restore[:,1],color='r',alpha=0.5)
plt.show()运行结果:
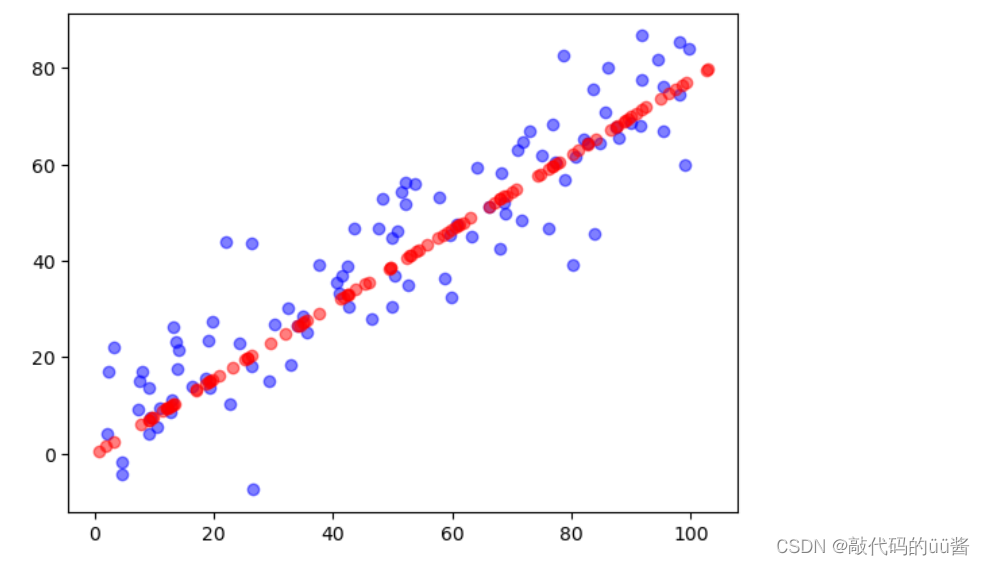
数据经过降维再恢复之后,就回到了我们的所有的数据点,此时所有的红色点都在一条直线上,但是每一个点是被一个二维特征表示的,即这些点在二维的平面上码成了一条直线,这就是用PCA降维的基本原理。
二、sklearn中的PCA
代码示例:
from sklearn.decomposition import PCA
pca = PCA(n_components=1)
pca.fit(X)
X_reduction = pca.transform(X) #降维
X_restore = pca.inverse_transform(X_reduction) #返回原来的维度
#绘图展示
plt.scatter(X[:,0],X[:,1],color='b',alpha=0.5)
plt.scatter(X_restore[:,0],X_restore[:,1],color='r',alpha=0.5)
plt.show()
运行结果:
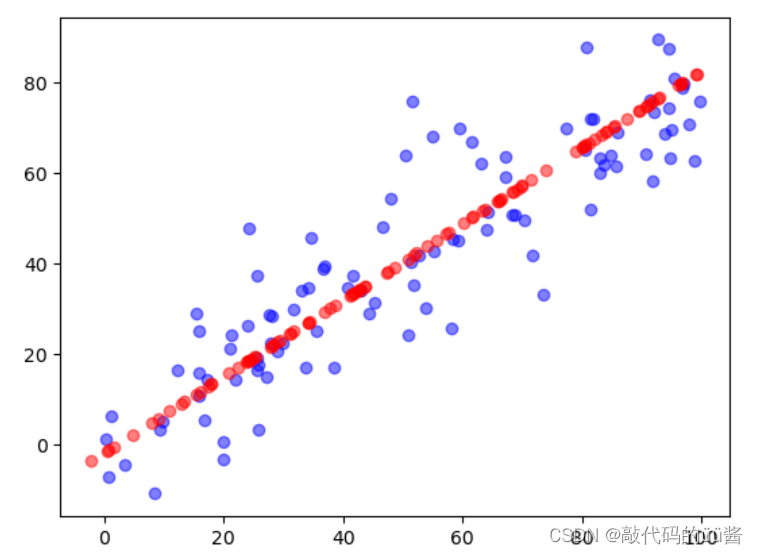
可以看到调用sklearn中的PCA类和我们自定义的PCA类训练结果是一致的。
代码示例:
#使用真实数据进行训练
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
digits = datasets.load_digits()
X = digits.data
y = digits.target
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 666)
# 使用KNN
%%time
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train,y_train)
knn_clf.score(X_test,y_test)
# 使用PCA降维
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X_train)
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
%%time
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction,y_train)
knn_clf.score(X_test_reduction,y_test)
运行结果:
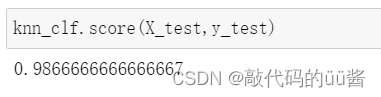

可以看出,我们将原来精度为64维的数据降维到2维,虽然降维之后大大的节省计算时间,但是数据精度却变得很低,显然2维太低了。基于此,PCA算法提供了一个数据指标explained_variance_ratio_,解释方差相应比例。

如上图所示,对于现在这个pca来说,它有两个维度,相应的比例分别约0.1和0.13。这代表两个轴中第一个轴它能解释大概14.5%元数据的方差,第二个轴可以解释大概13.7%。通过这样的两个数字,可以看出来对于我们的这两个维度来说,它涵盖了原数据相应总方差的14.5%+13.7%=28%左右,而剩下72%的那些方差信息就丢失了,显然丢失的信息过多。因此,我们可以通过这个变量来找到我们应该将我们的数据降到具体多少维度。
代码示例:
pca = PCA(n_components=X_train.shape[1])
pca.fit(X_train)
pca.explained_variance_ratio_运行结果:

这个运行结果一共有64个数值,并且从大到小依次排列的,它的意思就是:对于我们每一个主成分来说,依次的可以解释的方差是多少。可以看到最后一个轴是7×10的-34次,这个数字太小了,所以这个轴丢掉是无所谓的。但是第一个轴是0.14,也就是14%左右,因此它的占比是非常大的,那么这个数字近乎就可以表示每一个方向轴它对应的重要程度。
代码示例:
plt.plot([i for i in range(X_train.shape[1])],
[np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()运行结果:
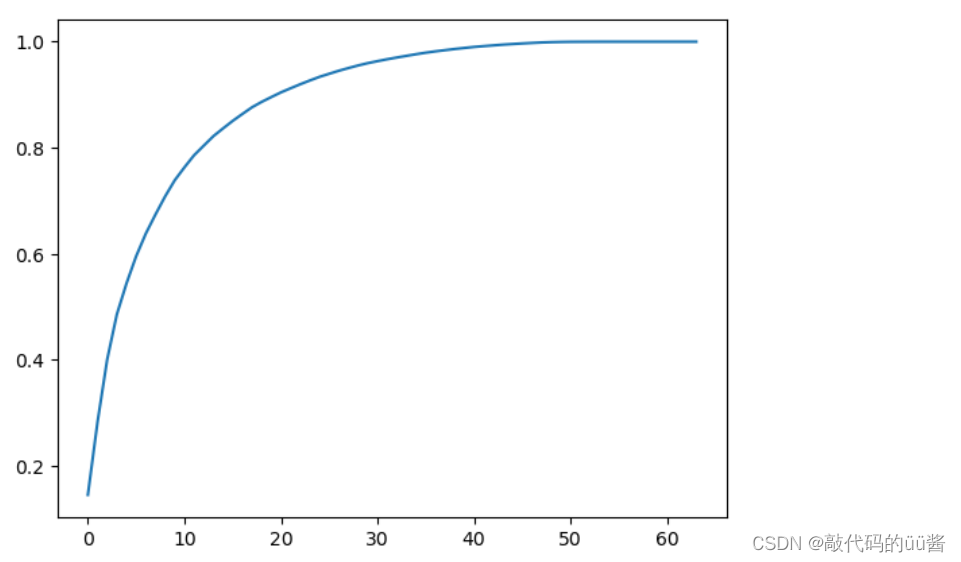
这个曲线的意思就是:假如我们取横轴前30个主成分的话,它能解释原来数据到底有多少方差,即保留了大概有多少个信息。相应的查这个曲线上对应的纵轴的点,可以看出有0.9+,也就是保留了90%多这样的信息。
因此,通过这个曲线可以根据我们的需求,来将数据降到具体的维度。比如,当我们希望我们的数据保持有95%以上的信息,那么我们只需在纵轴上找到0.95,然后相应的看横轴对应的那个数具体是多少即可。
代码示例:
pca = PCA(0.95,) #能解释原数据95%方差信息
pca.fit(X_train)
pca.n_components_
#运行结果:28
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
%%time
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction,y_train)
knn_clf.score(X_test_reduction,y_test)运行结果:

训练后的精度为0.98,它比我们使用全样本得到的这个识别率0.986666少了约0.66,但是在时间性能上却提高了十倍左右。因此,我们可以用这些时间来换取这个精度上稍微的丢失。





















 265
265

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








