面向无人机路径规划的多策略增强Dung Beetle优化（EDBO）

粪甲虫优化（DBO）是一种广受认可的受群体智能启发的元启发式算法，但在收敛速度和求解精度方面面临显著限制，特别是对于具有多个峰值的复杂多模态优化问题。
为了应对这些挑战，我们提出了增强的蜣螂优化（EDBO）算法，集成了四种创新机制：（1）最优值搜索引导策略，利用全局最佳解决方案来引导搜索并降低局部最优捕获的风险；（2）非线性动态调整因子，自适应地平衡探索和利用，以增强优化阶段的搜索多样性；（3）优先边界控制策略，动态细化边界行为，引导个体走向有希望的区域而不会停滞；（4）改进的觅食增强策略，结合自适应更新，以提高全局搜索效率并防止过早收敛。

1. 方法概述：原始 DBO 和提出的改进

本节简要介绍了原始 DBO 的行为及其相应的数学模型。此外，还详细探讨了提出的 EDBO 算法，包括最优值引导优化策略、非线性动态调整因子、新的优先边界控制策略和改进的觅食增强策略。

1.1. 原始 DBO

DBO 算法的设计灵感来自粪甲虫的各种行为模式，包括滚动球、跳舞、觅食、偷窃和繁殖。在该算法中，种群被分为四种不同类型的搜索代理，每种代理由一组独特的规则控制。

1.1.1. 滚球粪甲虫

粪甲虫将它们的粪球滚入球中，并利用太阳和月亮等天体线索高效导航。当遇到障碍物时，它们通常会爬上球顶并进行一系列舞蹈动作，帮助它们确定新的移动方向。相应的位置更新公式如下所示：

$$x_i(t+1)=x_i(t)+\alpha \times k\times x_i(t-1)+b\times \Delta x,$$

$$\Delta x=|x_i(t)-X^w|,$$

其中 $t$ 表示当前迭代次数，$x_i(t)$ 表示第 $i$ 次迭代中第 $i$ 只甲虫的位置。偏转系数 $k$ 是一个常数，限定在区间 (0, 0.2) 内，影响甲虫的方向偏移。同时，另一个常数 $b$ 在 0 和 1 之间变化，有助于计算位置。自然系数 $\alpha$，分配值为 1 或 -1，为更新机制引入了变异性。在优化的背景下，$X^w$ 表示全局最优位置，而 $\Delta x$ 模拟光强度的变化。

当粪甲虫在滚动其粪球时遇到障碍物时，它会进行一种独特的动作，通常称为“舞蹈”，以重新校准其方向并识别替代路线。这种行为模式在算法中通过一个切线函数反映出来，该函数复制了甲虫在遇到障碍物时评估新滚动方向的方式。因此，滚动粪甲虫的位置更新如下：

$$x_i(t+1)=x_i(t)+\tan (\theta )|x_i(t)-x_i(t-1)|,$$

其中，$\theta$ 表示偏转角，以弧度为单位，$\theta$ 限定在区间 [0, $\pi$] 内。

1.1.2. 繁殖球

一些由甲虫收集的粪球作为食物，而另一些则被滚到一个安全的地方产卵。如图 1 所示，这些被称为繁殖球，旨在孵化下一代。这些繁殖球周围的限制被严格定义如下：

$$L{b}^{\ast }=\max (X^{\ast }\times (1-R),Lb),$$

$$U{b}^{\ast }=\min (X^{\ast }\times (1-R),Ub),$$

图 1. 边界选择策略 I。

这里，当前局部最佳位置表示为 $X^{\ast }$，类似于粪甲虫产卵的最佳地点。产卵区域的下限 ($Lb$) 和上限 ($Ub$) 被指定为模仿甲虫产卵时选择的范围。因子 $R=1-t/T_{\max }$ 随算法迭代的进展而修改这些限制，其中 $t$ 表示当前迭代次数，$T_{\max }$ 表示最大迭代次数。这种调整反映了甲虫随着环境条件变化而变化的狭窄选择范围。此外，整体搜索空间被 $Lb$ 和 $Ub$ 限制，表示甲虫可以操作的最宽区域。

一旦繁殖球被运送到指定的产卵区域，雌性就会在其中产卵，每次迭代每只雌性产一个卵。繁殖球的位置更新如下：

$$B_i(t+1)=X^{\ast }+b_1\times (B_i(t)-L{b}^{\ast })+b_2\times (B_i(t)-U{b}^{\ast }).$$

在模型中，$B_i(t)$ 表示第 $i$ 个球在第 $t$ 次迭代中的位置，代表甲虫产下的繁殖球。为了引入随机性和变异性，反映自然过程中固有的不可预测性，使用了两个独立的随机向量 $b_1$ 和 $b_2$。每个向量的维度为 $1\times D$，其中 $D$ 表示问题的维度。

1.1.3. 小型粪甲虫

当小型甲虫在繁殖球内成熟时，它们会出来寻找食物。因此，需要划定一个最优的觅食区域来指导它们寻找食物，从而促进空间探索。如图 2 所示，这种最优觅食区域的边界定义如下：

$$L{b}^b=\max (X^b\times (1-R),Lb),$$

$$U{b}^b=\min (X^b\times (1-R),Ub),$$

图 2. 边界选择策略 II。

其中 $X^b$ 表示全局最优位置，作为目标觅食区域。该最优觅食区域的下限和上限分别被指定为 $Lb$ 和 $Ub$。因此，当小型甲虫觅食时，更新它们位置的公式定义如下：

$$x_i(t+1)=x_i(t)+C_1\times (x_i(t)-L{b}^b)+C_2\times (x_i(t)-U{b}^b),$$

其中 $x_i(t)$ 表示算法第 $t$ 次迭代中第 $i$ 只甲虫的位置。此外，$C_1$ 是从正态分布生成的随机数，并对甲虫的运动提供随机影响。$C_2$ 是一个随机向量，其分量在区间 (0,1) 内均匀分布，为位置更新增加更多的随机性。这种参数和变量的组合促进了甲虫觅食行为的真实模拟。

1.1.4. 偷窃粪甲虫位置更新

尽管并非所有甲虫都付出显著努力来推动粪球，但有些甲虫会参与偷窃它们。假设全局最优位置代表了此类盗窃甲虫最有利的目标，这些盗窃甲虫的位置更新公式如下：

$$x_i(t+1)=X^b+S\times g\times (|x_i(t)-X^{\ast }|+|x_i(t)-X^b|),$$

其中 $x_i(t)$ 表示算法第 $t$ 次迭代中第 $i$ 只“小偷”（一个隐喻性的代理）的位置。变量 $g$ 是从正态分布中抽取的随机向量，并设计为模拟小偷运动的不可预测性。此向量的维度为 $1\times D$，其中 $D$ 反映了问题的维度，确保随机性适当地应用于所有维度。$S$ 是算法中使用的常数值，以影响“小偷”代理的行为。

1.2. 改进的粪甲虫优化算法

1.2.1. 最优值搜索引导策略

对于原始 DBO 算法，从全局最差位置滚走的甲虫无法有效利用其能力。实际上，在搜索过程中引入全局最差位置可能会干扰高质量解的生成。全局最优解对于 DBO 算法至关重要。在原始算法中，如果甲虫个体在解空间中搜索时将最差解的信息纳入其中，这可能会使它们在最差解附近搜索。为了避免这个问题，我们通过以下方式改进了原始 (1)，(2)：用全局最优解替换更新规则中的全局最差解。具体公式如下：

$$x_i(t+1)=x_i(t)+\alpha \times k\times x_i(t-1)+b\times \Delta x,$$

$$\Delta x=|x_i(t)+\text{rand}\times x_{i1}^t|,$$

其中 $x_{i1}^t$ 表示当前迭代的全局最优解，$\text{rand}$ 表示 [0,1] 之间的随机数。与原始 DBO 公式相比，这种改进消除了全局最差解的负面影响，而是引导个体朝向全局最优解，从而增强优化过程。如图 3 所示，引入最优值搜索引导策略确保了更快地收敛到最优解，通过减少无效搜索和子最优区域来实现。这种方法通过随机数 $\text{rand}$ 提高了优化效率，并保持了多样性，防止过早收敛到局部最优。因此，该算法实现了更有效的全局探索和局部开发之间的平衡，增强了其整体全局搜索能力。

图 4. 最优值搜索引导策略。

1.2.2. 非线性动态调整因子

在原始粪甲虫繁殖行为中，权重 $R$ 线性调整为 $R=1-t/T_{\max }$。这种线性调整提供了一种简单而合乎逻辑的方法，通过逐渐减少算法过程中初始边界个体的影响来平衡探索和开发。然而，这种策略在复杂优化场景中表现出显著限制。

首先，线性衰减可能导致权重过早降低到较低水平，这意味着算法可能开始专注于局部区域的详细搜索，而没有充分探索整个搜索空间。这种过早收敛在多峰优化问题中尤其成问题，其中不足的探索可能导致次优解。其次，边界个体的渐进性忽视可能导致错过搜索空间边缘或外部区域的更好解决方案。最后，线性衰减公式的可预测性和确定性限制了算法对新发现的有希望区域的适应性。

为了解决这些限制，提出了一种非线性动态调整因子，引入了非线性衰减和随机扰动，以增强算法的灵活性和适应性，如图 4 所示。具体公式如下：

$$R=1-\text{rand}\times {\left(\frac{t}{T_{\max }}\right)}^2,$$

其中 $\text{rand}$ 表示 [0,1] 之间的随机数。与原始线性衰减相比，这种非线性策略确保了 $R$ 不会单调或可预测地减少。通过引入随机性，非线性动态调整因子确保了权重的减少不再单调或可预测，增强了算法对不同优化阶段的适应性。与通常在算法如 WOA 和 GSA 中使用的固定或正弦权重调整策略不同，EDBO 中的非线性衰减提供了二次转换机制，允许从广泛探索到精确开发的逐步转变。这种自适应行为使算法能够动态响应新发现的有希望区域，确保有效的全局搜索，同时保留重新访问初始边界的灵活性。通过随机因子调节权重的快速减少，使算法能够在发现更有希望的区域时快速响应，同时在必要时仍考虑初始边界。此外，算法可以通过调整权重减少的速率更有效地平衡全局搜索和局部开发，特别是在迭代初期保持更广泛的探索能力。

图 5. 非线性动态调整因子。

1.2.3. 优先边界控制策略

在迭代过程中，种群中的个体经常超过预定的搜索边界。在传统的 DBO 算法中，这些越界个体简单地被放置在搜索空间的上下限。尽管这种方法简单，但它未能有效利用这些个体的位置信息，并且常常导致它们随机运动趋势和潜在搜索方向的丧失。因此，为了最大化利用这些位置信息，提出了一种改进策略，通过调整超出边界的个体的位置来使用当前全局最优解的位置，如图 5 所示。

$$\begin{array}{rl}& x_i(t+1)=\text{rand}\times x_{i1}^t,x<lb,\\ & x_i(t+1)=(1-\text{rand})\times x_{i1}^t,x>ub,\text{and}\end{array}$$

其中 $x_{i1}^t$ 表示当前迭代的全局最优解，$\text{rand}$ 是 [0,1] 之间的随机数。

图 6. 优先边界控制策略。

其中 $x_{i1}^t$ 表示当前迭代的全局最优解，$\text{rand}$ 是 [0,1] 之间的随机数。这种策略利用随机性来处理越界个体，增强算法的随机性并帮助其避免局部最优，从而允许在搜索过程中探索更多潜在区域。该公式通过位置调整引入随机性，确保个体不仅被限制在边界内，而是被引导向全局最优解。图 5 说明了这种调整过程，其中越界个体根据全局上下文重新定位，提高算法的搜索效率。

总之，优先边界控制策略不仅提高了位置信息使用的效率，还增强了算法在复杂搜索空间中的适应性和探索能力。使用这种策略，更有可能在全球范围内找到最优解，并避免因边界约束而错过优化机会。

1.2.4. 改进的觅食增强策略

为了减轻过度聚集和陷入局部最优的问题，必须使种群能够动态地逃离当前状态并探索搜索空间的不同区域。尽管原始 DBO 算法利用高斯扰动来促进位置更新的随机性并最小化立即陷入的风险，但它们缺乏适应算法在不同优化阶段变化的探索和开发需求的能力。这种静态策略限制了算法的整体性能，特别是在解决复杂、多模态优化问题时。

相比之下，鹈鹕优化算法 [26] 以其简单的参数配置和强大的性能而闻名，特别是在探索阶段。它可以有效扫描和定位猎物（即搜索空间中的潜在最优解），表现出优异的优化能力。然而，鹈鹕优化算法中的下一代个体更新仅依赖于前一代个体的位置。这种盲目的运动策略降低了解决方案多样性，并可能严重影响优化效率。

为了解决这些限制，本研究将鹈鹕优化算法的探索特性与改进的觅食增强策略相结合。该策略修改了原始 DBO 更新机制，以自适应地平衡探索和开发，同时保留原始 DBO 更新机制。觅食增强策略在觅食阶段以 50% 的概率激活，确保已知最优路径的探索和新潜在区域的探索。这种自适应机制显著增加了逃离局部最优的可能性，从而提高了算法解决复杂优化问题的性能。具体公式如下：

$$x_i(t+1)=x_i(t)+\text{rand}\times (x_{i1}^t-l\times x_i(t)),$$

其中 $x_{i1}^t$ 表示当前迭代的全局最优解，$\text{rand}$ 是 [0,1] 之间的随机数，$l$ 表示等于 1 或 2 的随机整数。这些随机元素的引入确保了算法可以根据当前状态自适应地调整其搜索行为。

在探索阶段（早期迭代），随机因子 $\text{rand}$ 和参数 $l$ 促进了多样化的运动模式，使算法能够在搜索空间中广泛搜索。这降低了过早收敛的可能性，并增强了算法逃离局部最优的能力。在开发阶段（后期迭代），全局最优解 $x_{i1}^t$ 的影响变得更加显著，指导搜索向解空间中更有希望的区域进行细化。通过引入这种自适应机制，策略在复杂优化景观中保持了探索和开发的动态平衡。

这种机制不仅增强了搜索过程的灵活性，还提高了算法的整体优化效率，如第 X 节的实验结果所示。引入的改进觅食增强策略在解决多模态和高维优化问题时特别有效。

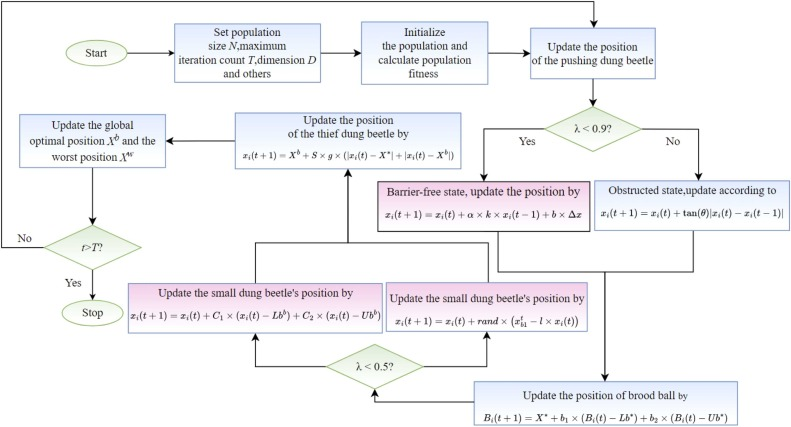
为了更深入地了解 EDBO 的工作原理，流程图如图 6 所示，其伪代码详细在算法 1 中展示。

2.1.2. 数学模型

设无人机飞行的起点表示为 $(x_s,y_s,z_s)$，终点表示为 $(x_e,y_e,z_e)$。基于三次样条插值，通过 $g$ 个离散点 $(x_s,y_s,z_s),(x_1,y_1,z_1),...,(x_{g-1},y_{g-1},z_{g-1}),(x_e,y_e,z_e)$ 生成一条平滑曲线。该曲线随后表示为一系列离散点 $(h1,h2,...,hg)$，其中 $hm$ 的坐标为 $(x_m,y_m,z_m)$。因此，该问题的目标函数可以推导如下 [34]：

$$F_{lc}=w_1\times F_{pc}+w_2\times F_{hc}+w_3\times F_{ac},$$

其中 $F_{lc}$ 表示总成本，$F_{pc}$ 表示路径长度的成本，$F_{hc}$ 表示高度标准差的成本，$F_{ac}$ 表示规划路径平滑度的成本，$w_i(i=1,2,3)$ 是权重。权重系数的约束条件如公式 (19) 所示。

$$\{\begin{array}{l}{w}_i\ge 0\\ {\sum }_{i=1}^3{w}_i=1\end{array}$$

通常，无人机飞行需要节省时间并尽可能减少成本，同时确保安全，因此路径规划的长度至关重要。无人机的数学模型如公式 (20) 所示，

$$F_{pc}=\Vert (x_{m+1},y_{m+1},z_{m+1})-(x_m,y_m,z_m){\Vert }_2,$$

其中 $(x_m,y_m,z_m)$ 表示无人机规划路径中的第 $m$ 个航点。

此外，无人机的飞行高度对控制系统和安全性有很大影响，因此我们需要考虑这一因素的影响。公式 (21) 表示数学模型。

$$F_{hc}=\sqrt{\sum _{m=1}^g{\left(z_m-\frac{1}{n}\sum _{k=1}^g{z}_m\right)}^2}.$$

最后，我们还需要考虑无人机转弯时的影响，数学模型如公式 (22) 所示。

$$F_{ac}=\sum _{m=1}^{g-2}\left(\arccos \left(\frac{{\vec{\phi }}_{m+1}\cdot {\vec{\phi }}_m}{|{\vec{\phi }}_{m+1}|\times |{\vec{\phi }}_m|}\right)\right),$$

其中 ${\vec{\phi }}_m$ 表示 $(x_{m+1}-x_m,y_{m+1}-y_m,z_{m+1}-z_m)$。

总之，我们可以得到无人机路径规划优化问题的模型，如公式 (23) 所示。

$$\begin{array}{r}\min F_{lc}(L)\\ \text{s.t., path}(L)\notin \text{Ground}\cup \text{Obstacle},\end{array}$$

其中 $L$ 表示可飞行路径，$\text{Ground}$ 和 $\text{Obstacle}$ 分别表示地面和障碍物。在本文中，我们用公式 (24) 模拟地面和障碍物集。

$$z=\sin (y+1)+\sin (z)+\cos (x^2+y^2)+2\times \cos (y)+\sin (x^2+y^2),$$

2.1.2. 仿真实验

在本研究中，我们分别将 $w_1$、$w_2$ 和 $w_3$ 赋值为 0.4、0.3 和 0.3。无人机的起点设为 (0, 0, 20)，终点设为 (200, 200, 30)。使用三次样条插值，我们生成了一条可行且平滑的路径，并将其与各种竞争方法进行了比较。实验参数保持与前几节 [35] 中概述的一致。我们记录了计划路径的最佳、最差、平均、标准偏差和排名值，结果详细列于表 12 中。