IEEE TPS | 论文速递！KDD-RL——知识数据驱动的混合强化学习方法，用于解决电力系统的OPF问题

最新推荐文章于 2024-12-02 10:35:05 发布

小天才学习机打游戏

最新推荐文章于 2024-12-02 10:35:05 发布

阅读量1k

点赞数 10

文章标签：人工智能机器学习算法神经网络 ocr rnn 架构

本文链接：https://blog.csdn.net/m0_59164520/article/details/143027332

版权

创新点

本文提出了一种知识数据驱动的混合强化学习(KDD-RL)方法来解决电力系统实时运行中的顺序OPF问题。首先，将最先进的强化学习算法用于在不准确的环境下有效地制定调度命令。然后，利用混合知识数据驱动的安全层将简单的调度命令投影到安全区域，保证了电力系统的安全约束不被破坏。

图1 提出的方法示意图

与已有的研究成果相比，本研究的主要贡献总结如下:

优化与强化学习的结合: 综合利用强化学习方法在高效决策方面的优势和优化方法在尊重安全限制方面的优势；
混合知识-数据驱动: 安全层制定的投影模型以先验知识初始化，并根据最新经验不断更新，提高了系统在无经验突发场景下的安全性，提高了模型长期运行的准确性；
安全层加速: 安全层采用基于优化的线性投影模型和快速非活动约束识别方法，消除了冗余约束，加快了算法的建模和计算过程；
有功与无功的协调: 本文研究了考虑有功与无功协调调度的交流环境下的OPF问题。所提出的方法是通用的，可以很容易地扩展到其他情况下的电力系统运行，如经济调度、能源管理、电力跟踪和电压调节。

1. 摘要

针对环境模型的不准确性和不完善性，本文提出了一种知识数据驱动的混合强化学习(KDD-RL)方法来解决实时运行过程中的顺序最优潮流问题。提出了一种改进的软动作-评价算法，用于训练控制策略和制定对发电机的顺序调度命令。为了促进强化学习算法的安全探索，开发了一个混合的知识数据驱动的安全层，将不安全的动作转换为安全区域。此外，为了提高安全层的计算效率，提出了一种具有非活动约束识别过程的安全约束线性投影模型。数值仿真结果验证了该方法在提高决策效率、促进电力系统安全运行方面的优越性和可扩展性。

关键词：最优潮流，经济调度，强化学习，安全层

2. RL方法的框架和方法

所提出的KDD-RL方法解决顺序实时OPF问题的技术路线如图2所示。这个问题用MDP问题来描述。电力系统的状态信息有两种使用方式。它首先用于更新安全层中的参数，以确保安全层捕获最新的系统约束。此外，当前和历史状态都存储在一个优先经验回放中，并用于通过小批量更新和推理进行强化学习模型训练，以生成下一轮的动作（简单的调度命令）。随后，简单的调度命令被转发到安全层，以生成最终的安全动作（安全调度命令），该命令用于电力系统。所提出的方法由改进的软动作-评论（soft actor-critic, SAC）算法和混合知识-数据驱动的安全层组成。改进的SAC算法用于训练控制策略并制定调度命令。为了确保电力系统的安全，开发了一种混合知识-数据驱动的安全层，将不安全的动作转化为安全区域。安全层和SAC中的神经网络根据来自环境的最新数据积累以顺序方式进行更新，这进一步促进了训练策略的长期经济和安全运行。

值得注意的是，本研究中有两种不同类型的动作。第一种类型的动作由策略网络输出（在进入安全层之前），第二种类型的动作由安全层输出。为了避免歧义，以下文本中将第一种类型称为“动作”，将第二种类型称为“安全动作”。需要注意的是，为了确保神经网络的可微性并促进梯度反向传播过程，第一种类型的动作被存储在重放缓冲区中，并用于SAC算法的训练过程。因此，安全层确实会影响SAC算法的可微性，因为它不会干扰梯度反向传播的流动。

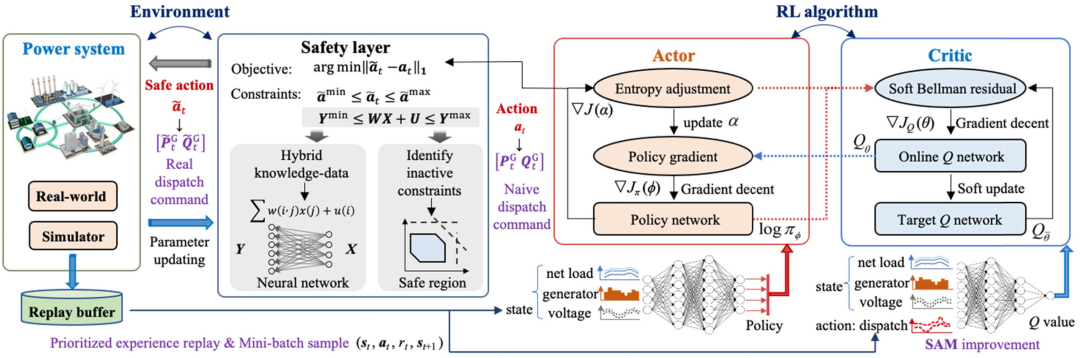
图2 提出的KDD-RL方法的框架

3. 安全层的描述

在安全层中描述了一种加速的混合知识-数据驱动投影方法，通过该方法，危险动作被转换为安全区域，以促进电力系统的安全运行。安全约束线性投影模型在A节中进行了描述。在B节和C节中，安全层中的电力流安全约束使用先验知识进行初始化，并根据从环境中测量的最新数据进行更新。D节提出了无效约束的识别方法。与现有的安全层文献相比，所提方法的优势和新颖性如下：

i) 与现有的基于数据驱动的安全层相比，所提的安全层能够充分利用专家知识和数据挖掘各自的优势。专家知识用于对安全层中的安全约束进行热启动，为经验不足的突发情况提供指导。数据驱动的方法进一步用于动态更新安全层参数，以提高模型的准确性。

ii) 所提的方法是一个线性模型，具有较低的非线性和更高的计算效率，这与现有的基于二次规划的安全层有很大不同。

iii) 带有严格数学证明的非活动约束识别方法新近被纳入安全层中，这一方法消除了非活动约束，并进一步降低了现有文献中安全层的计算复杂性。

A. 安全约束线性投影模型

本小节讨论基于优化的安全约束线性投影模型，以将不安全的操作转换为安全区域。目标定义如下:

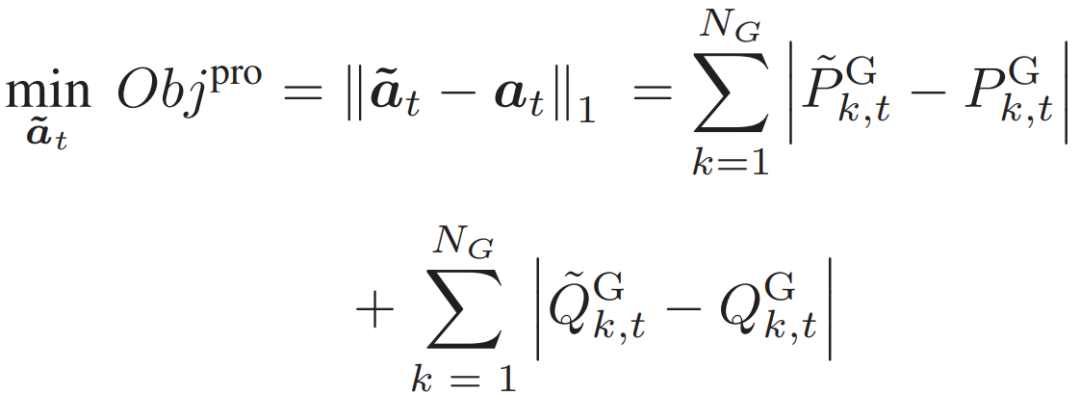
其中，是安全动作向量，由安全调度指令组成，指向发电机的有功功率输出 (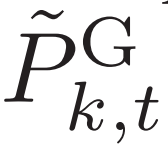) 和无功功率输出 (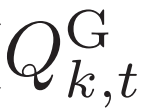)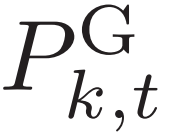；和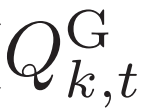是发电机的有功功率输出和无功功率输出的初步调度指令，这些指令由强化学习算法的动作-评价网络输出。

B. 混合知识-数据驱动的安全操作约束更新

为了量化动作与安全操作限制之间的关系，用先验知识初始化矩阵(W和U)，并根据来自环境的最新数据测量作为神经网络进行更新。

1. 基于专家知识的初始化: 在早期训练阶段或一些没有经验的突发情况下，根据系统的先验知识初始化安全操作约束(33)中的系数矩阵(W和U)。采用[38]中提出的线性化潮流方程初始化安全层的安全运行约束，如下所示:

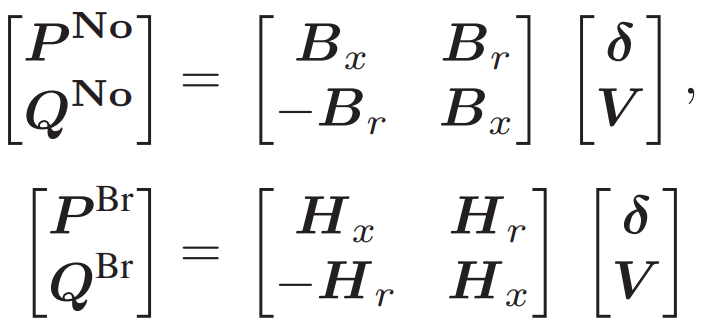
其中，和是有功功率和无功功率注入向量；δ 和 V 是节点角度和电压幅值向量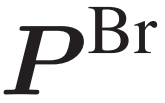；和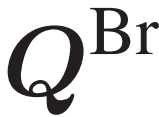是支路有功功率流和无功功率流向量。

2.数据驱动的参数更新方法: 根据[21]，采用单层全连接神经网络近似复杂的交流环境。考虑_W_、U、X、Y 分别作为权重参数、偏置参数、输入向量、输出向量，与单层全连接神经网络一致。神经网络参数可以通过(39)中矩阵w和u的元素进行初始化。神经网络参数通过最小化真实环境测量值与神经网络输出值之间的均方误差来优化。

与纯数据驱动的方法相比，安全层中的安全操作约束是通过先验知识初始化的。这可以显著提高在缺乏训练数据的未经验场景中的行动安全性，即在早期训练阶段和应急场景中。此外，一旦环境测量值与神经网络输出之间的累积误差超过可接受的阈值，神经网络将被触发重新训练，使用最新数据进一步更新网络参数并提高模型准确性，如图3所示。

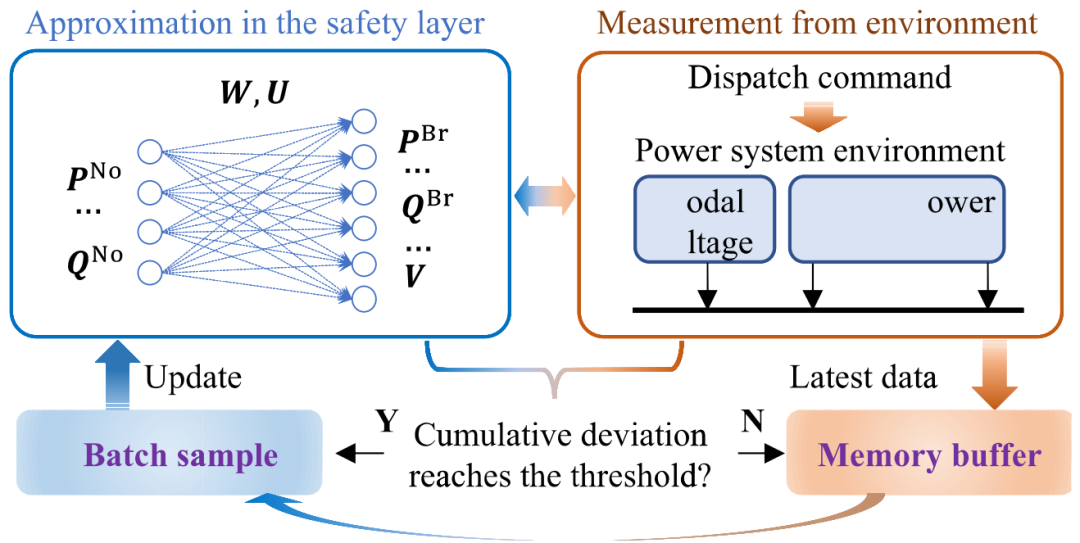
图3 安全层神经网络参数在线更新

根据 [21-23] 的研究，神经网络中不考虑激活函数，以避免在安全层中引入非线性。此外，神经网络参数的结构与（39）中的传输矩阵相同。因此，神经网络参数可以用于更新传输矩阵中的参数，并建模节点功率注入（X）与功率流状态（Y）之间的关系。

需要注意的是，神经网络的线性近似值与从交流环境中测得的真实值之间不可避免地存在误差。在本研究中，处理线性化误差的方法总结如下：

i) 从专家知识中得到的线性化功率流模型被用于初始化安全层中的神经网络。专家知识已在许多基于优化的最优潮流（OPF）问题中得到应用。因此，即使在早期训练阶段或缺乏经验的应急场景中，所提出的安全层也能实现与传统基于优化的 OPF 方法相当的准确性。

ii) 基于知识驱动的线性化功率流模型，本研究根据来自真实环境的最新数据测量更新神经网络参数，这可以进一步提高线性模型的准确性。此外，如果仍然存在不可避免的约束违反场景，可以通过修改 (33) 中安全约束的可接受范围来计算一个保守解，以抵消近似误差。

iii) 功率流状态 () 的计算公式为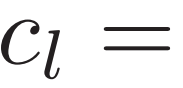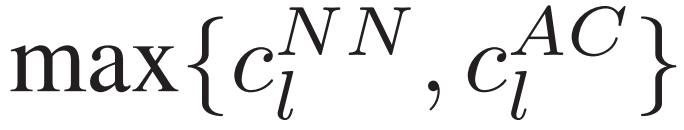，其中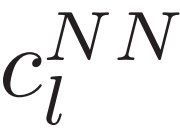代表安全层中神经网络预测的线性近似值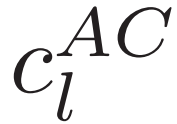，代表从电力系统的交流环境中测得的真实数据。因此，安全层通过影响奖励函数中定义的安全约束违反值，间接影响 SAC 训练过程。为了减轻真实环境中的安全约束违反，并缓解线性近似误差带来的不利影响，利用安全层中的线性近似值 (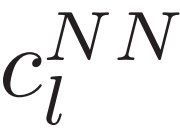) 和交流环境中的真实值 (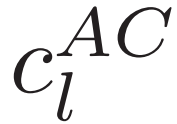) 之间较差的功率流状态来更新 (17) 中的奖励 (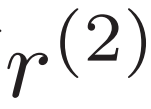) 和 (25) 中的惩罚系数 (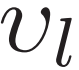)。因此，安全约束违反的惩罚受到安全层预测值和电力系统环境真实数据的综合影响。

C. 非激活约束识别方法

大多数约束是无效的，不影响优化问题的可行域和最终解。例如，在[40]中，神经网络通过元启发式算法进行训练，并用于预测安全约束的OPF问题中必要的保护伞约束。在数学推导和灵敏度分析的基础上，[41]提出了一种用于机组承诺问题的非激活约束快速识别方法。同样，(33)中的系统安全约束占安全层约束的绝大部分。这些非活动安全约束不影响优化结果，但显著增加了建模和计算过程的复杂性和负担。鉴于此，本节提出了一种快速识别方法，消除冗余的安全约束，从而大大简化了安全层的优化问题。

在本节中提出并证明了所提出的非激活约束识别方法。(33)可重新排列如下:

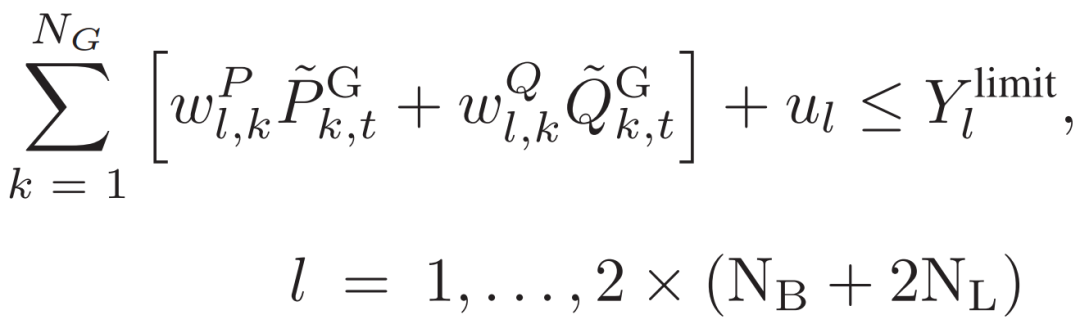
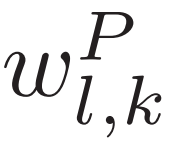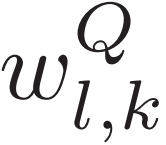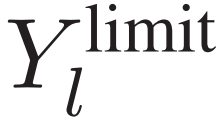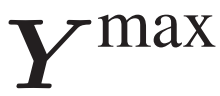其中，和是W矩阵中的系数;ul是矩阵U中的系数;表示矩阵和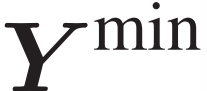中的系数;为了便于后续推导的解释，将(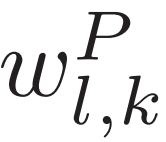和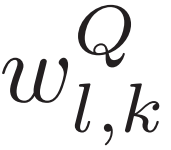)的系数由大到小进行排列，即; 。

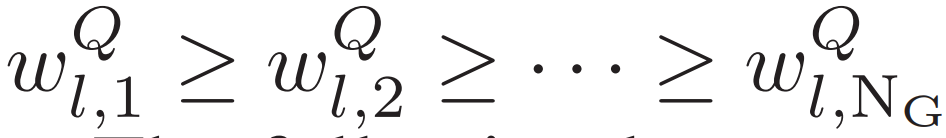D. 安全层的实现过程

所提出的安全层的实现流程图如图4所示。

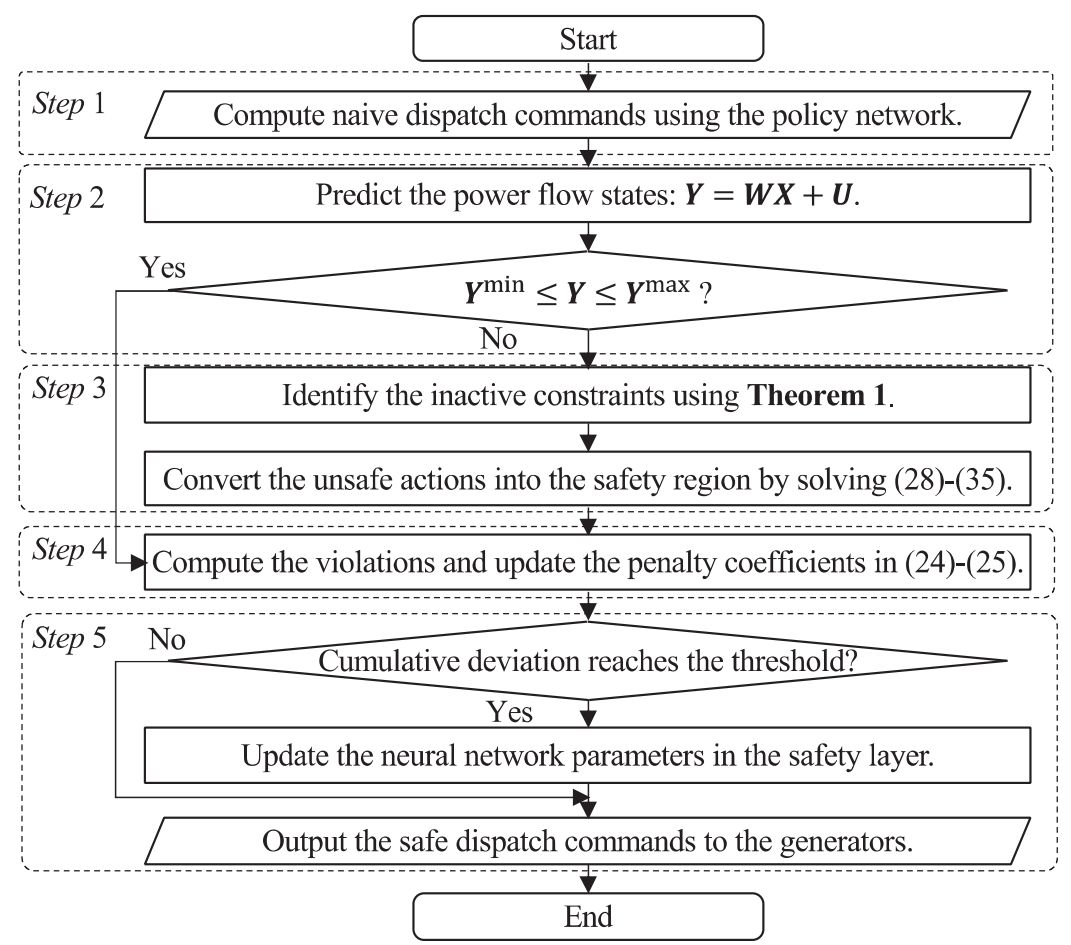
图4 安全层的实现过程

步骤 1：进行动作推断。通过强化学习算法学习的策略网络计算出初步调度指令。

步骤 2：预测功率流状态。将初步调度指令和节点负荷预测作为输入，使用安全层中的神经网络预测近似的功率流状态（Y）。如果功率流状态的预测值超过限制值，则进入步骤 3；否则，进入步骤 4。

步骤 3：求解安全约束线性投影问题。通过求解优化基础的安全约束线性投影问题，将不安全的动作转换为安全区域。将满足安全约束的安全调度指令发送给发电机。

步骤 4：更新惩罚系数。通过计算约束违规情况，更新惩罚系数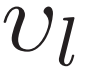（）的梯度。

步骤 5：更新神经网络。如果近似值与测量值之间的累计偏差超过阈值，则通过最小化均方误差对安全层中的神经网络进行微调。

｜总结

本文提出了一种混合知识数据驱动的强化学习方法。该方法能够在不依赖精确环境参数的情况下快速决策，解决连续实时OPF问题。通过将专家知识与非活动约束识别过程相结合，建立了改进的线性投影模型，提高了动作的安全性，提高了系统在早期训练阶段和缺乏经验的突发情况下的安全性。通过与现有文献的比较，从理论上和数值上验证了该方法在提高决策效率和促进电力系统安全运行方面的优势。

如何学习大模型 AI ？

由于新岗位的生产效率，要优于被取代岗位的生产效率，所以实际上整个社会的生产效率是提升的。

但是具体到个人，只能说是：

“最先掌握AI的人，将会比较晚掌握AI的人有竞争优势”。

这句话，放在计算机、互联网、移动互联网的开局时期，都是一样的道理。

我在一线互联网企业工作十余年里，指导过不少同行后辈。帮助很多人得到了学习和成长。

我意识到有很多经验和知识值得分享给大家，也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

在这里插入图片描述