Adam优化器
同时引入了SGDM的一阶动量和RMSProp二阶动量。
m
t
=
β
1
∗
m
t
−
1
+
(
1
−
β
1
)
∗
g
t
m_t=β_1*m_{t-1}+(1-β_1)*g_t
mt=β1∗mt−1+(1−β1)∗gt
修正一阶动量的偏差: m t ^ = m t 1 − β 1 t 修正一阶动量的偏差:\widehat{m_t}=\frac{m_t}{1-β^t_1} 修正一阶动量的偏差:mt =1−β1tmt
V t = β 2 ∗ V s t e p − 1 + ( 1 − β 2 ) ∗ g t 2 V_t=β_2*V_{step-1}+(1-β_2)*g^2_t Vt=β2∗Vstep−1+(1−β2)∗gt2
修正二阶动量的偏差: V t ^ = m t 1 − β 2 t 修正二阶动量的偏差:\widehat{V_t}=\frac{m_t}{1-β^t_2} 修正二阶动量的偏差:Vt =1−β2tmt
η t = l r ∗ m t ^ V t ^ = l r ∗ m t 1 − β 1 t / V t 1 − β 2 t η_t=lr*\frac{\widehat{m_t}}{\sqrt{\widehat{V_t}}}=lr*\frac{m_t}{1-β^t_1}/\sqrt{\frac{V_t}{1-β^t_2}} ηt=lr∗Vt mt =lr∗1−β1tmt/1−β2tVt
参数更新公式: w t + 1 = w t + η t = w t − l r ∗ m t 1 − β 1 t / V t 1 − β 2 t 参数更新公式:w_{t+1}=w_t+η_t=w_t-lr*\frac{m_t}{1-β^t_1}/\sqrt{\frac{V_t}{1-β^t_2}} 参数更新公式:wt+1=wt+ηt=wt−lr∗1−β1tmt/1−β2tVt
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化loss曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time ##1##
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
##########################################################################
m_w, m_b = 0, 0
v_w, v_b = 0, 0
beta1, beta2 = 0.9, 0.999
delta_w, delta_b = 0, 0
global_step = 0
##########################################################################
# 训练部分
now_time = time.time() ##2##
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
##########################################################################
global_step += 1
##########################################################################
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
##########################################################################
# adam
m_w = beta1 * m_w + (1 - beta1) * grads[0]
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])
m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))
w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))
##########################################################################
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
total_time = time.time() - now_time ##3##
print("total_time", total_time) ##4##
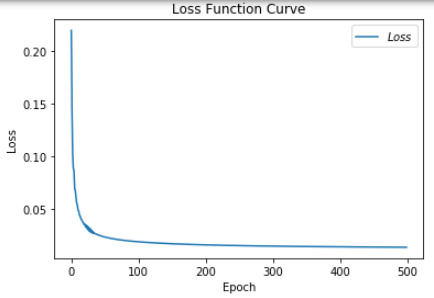
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
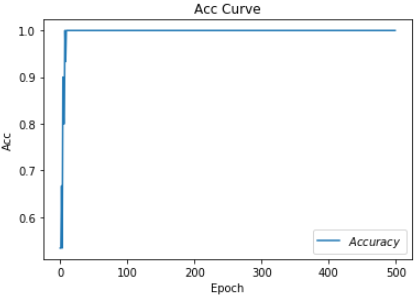
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()
.
.
.
Epoch 488, loss: 0.0139629568438977
Test_acc: 1.0
--------------------------
Epoch 489, loss: 0.013959497911855578
Test_acc: 1.0
--------------------------
Epoch 490, loss: 0.013956061913631856
Test_acc: 1.0
--------------------------
Epoch 491, loss: 0.013952645822428167
Test_acc: 1.0
--------------------------
Epoch 492, loss: 0.013949236366897821
Test_acc: 1.0
--------------------------
Epoch 493, loss: 0.013945839717052877
Test_acc: 1.0
--------------------------
Epoch 494, loss: 0.013942447141744196
Test_acc: 1.0
--------------------------
Epoch 495, loss: 0.013939081109128892
Test_acc: 1.0
--------------------------
Epoch 496, loss: 0.01393572788219899
Test_acc: 1.0
--------------------------
Epoch 497, loss: 0.01393237872980535
Test_acc: 1.0
--------------------------
Epoch 498, loss: 0.013929049717262387
Test_acc: 1.0
--------------------------
Epoch 499, loss: 0.013925729785114527
Test_acc: 1.0
--------------------------
total_time 8.95842695236206
论文解析:ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION
ADAM:自适应距估计

两位作者分别来自OpenAi和Toronto University。
摘要

摘要主要介绍了Adam算法的一些优点,具体来说就是执行起来很容易、计算非常高效、需要的内存很少而且对于梯度对角缩放具备不变性,非常适合解决大规模数据和参数优化的问题,另外也适于非平稳和非凸优化的这种问题,解决起来即使是很高噪声或者是稀疏梯度的问题,也有很好的效果,另外还有一个特点就是它的超参数可以很直观的解释,并且基本上只需要非常少量的调参。
后面给出了理论的收敛性的一些验证啊,还有实验结果。
背景

正文第一段是背景介绍,基于随机梯度的优化在许多科学和工程领域都具有核心的实用性,那许多问题都可以看作是一些标量参数目标函数的优化,也就是求最大化或者最小化的问题,我们知道这个问题说起来很容易,让计算机实验起来会遇到许多困难,比如局部最小值,高原、鞍点、平坦区域、悬崖会产生梯度消失与梯度爆照的问题,另外还有初始点选择错误导致的难以优化等等,所以梯度下降问题依然非常值得研究,但这里作者提到了 stochastic gradient descent,也就是标准的随机梯度下降算法,他已经证明了SGD非常高效而且有效的优化方法,本文的主要目的是介绍了一种高维参数空间的随机目标优化问题,在这种情况下,高阶的优化方法不太合适了,因为太复杂了,这里仅仅使用了一阶的方法。

第二段他说我们提出了Adam算法,这是一种有效的随机优化方法,只需要一阶梯度,而且内存的需求量非常小,具体来说呢,该方法跟据梯度的一阶矩阵和二阶矩阵来估计计算不同参数的个体自适应学习率。Adam这个名字是来源于adaptive moment estimation(自适应矩估计),它其实是把两种很流行的算法一个AdaGrad、一个是RMSProp这两种算法结合到了一起。
算法介绍

参数解读:
g
t
⨀
g
t
:
两个向量逐个元素的乘积
t
:
步数
α
:学习率
θ
:参数
f
(
θ
)
:
目标函数
,
也就是损失函数
g
t
:
梯度,对目标函数求导
∂
f
∂
θ
β
1
:一阶矩衰减系数
(
指数衰减系数
)
β
2
:二阶矩指数衰减系数
m
t
:
一阶矩
(
g
t
的均值
)
v
t
:
二阶矩
(
g
t
的方差
)
m
t
^
:
m
t
偏执矫正
v
t
^
:
v
t
的偏执矫正
{gt}\bigodot{gt}:两个向量逐个元素的乘积\\t:步数\\α:学习率\\θ:参数\\f(θ):目标函数,也就是损失函数\\g_t:梯度,对目标函数求导\frac{\partial f}{\partial θ}\\β1:一阶矩衰减系数(指数衰减系数)\\β2:二阶矩指数衰减系数\\m_t:一阶矩(g_t的均值)\\v_t:二阶矩(g_t的方差)\\\widehat{m_t}:m_t偏执矫正\\\widehat{v_t}:v_t的偏执矫正
gt⨀gt:两个向量逐个元素的乘积t:步数α:学习率θ:参数f(θ):目标函数,也就是损失函数gt:梯度,对目标函数求导∂θ∂fβ1:一阶矩衰减系数(指数衰减系数)β2:二阶矩指数衰减系数mt:一阶矩(gt的均值)vt:二阶矩(gt的方差)mt
:mt偏执矫正vt
:vt的偏执矫正
算法解析:
t
←
t
+
1
:
更新步数
g
t
←
∇
θ
f
t
(
θ
t
−
1
)
:
求梯度
m
t
←
β
1
∗
m
−
1
+
(
1
−
β
1
)
∗
g
t
:
求一阶矩,也就是过往梯度与当前梯度的均值
,
m
t
−
1
是前一步的均值,
g
t
是当前的梯度
物理意义上是计算一阶动量,类似平滑,通过保持这个匀速直线运动方向上的惯性,来使得一阶矩的更新
v
t
←
β
2
∗
v
t
−
1
+
(
1
−
β
2
)
∗
g
t
2
:求二阶矩,也就是过往梯度的平滑与当前梯度平方的均值,也就是转动惯量的持续平滑
m
t
^
←
m
t
1
−
β
1
t
v
t
^
←
v
t
1
−
β
2
t
对
m
t
和
v
t
的一个矫正,随时间的增大分数值越来越小,相当于学习率,学习的步长越来越小
θ
t
←
θ
t
−
1
−
α
∗
m
t
^
v
t
^
+
ϵ
:
更新参数
θ
,
ϵ
是为了防止分母为
0
,
t\leftarrow{t+1}:更新步数\\ g_t\leftarrow{∇_θf_t(θ_{t-1})}:求梯度\\ m_t\leftarrow{β_1*m-1+(1-β_1)*g_t}:求一阶矩,也就是过往梯度与当前梯度的均值,m_{t-1}是前一步的均值,g_t是当前的梯度\\ 物理意义上是计算一阶动量,类似平滑,通过保持这个匀速直线运动方向上的惯性,来使得一阶矩的更新\\ v_t\leftarrowβ_2*v_{t-1}+(1-β_2)*g_t^2:求二阶矩,也就是过往梯度的平滑与当前梯度平方的均值,也就是转动惯量的持续平滑\\\widehat{m_t}\leftarrow{\frac{m_t}{1-β_1^t}} \\\widehat{v_t}\leftarrow{\frac{v_t}{1-β_2^t}}\\ 对m_t和v_t的一个矫正,随时间的增大分数值越来越小,相当于学习率,学习的步长越来越小\\ θ_t\leftarrowθ_{t-1}-{\frac{α*\widehat{m_t}}{\sqrt{\widehat{v_t}}+ϵ}}:更新参数θ,ϵ是为了防止分母为0,
t←t+1:更新步数gt←∇θft(θt−1):求梯度mt←β1∗m−1+(1−β1)∗gt:求一阶矩,也就是过往梯度与当前梯度的均值,mt−1是前一步的均值,gt是当前的梯度物理意义上是计算一阶动量,类似平滑,通过保持这个匀速直线运动方向上的惯性,来使得一阶矩的更新vt←β2∗vt−1+(1−β2)∗gt2:求二阶矩,也就是过往梯度的平滑与当前梯度平方的均值,也就是转动惯量的持续平滑mt
←1−β1tmtvt
←1−β2tvt对mt和vt的一个矫正,随时间的增大分数值越来越小,相当于学习率,学习的步长越来越小θt←θt−1−vt
+ϵα∗mt
:更新参数θ,ϵ是为了防止分母为0,
更新参数θ的过程,就好比在崎岖不平的山路上开越野车,那么一阶矩就是控制的方向盘往前开,实现动量的平滑,因为动量就是衡量物体在一个直线运动方向上保持运动的趋势, 二阶矩就是控制左右旋转方向,或者说利用惯性让车往左右转的时候更加平滑,也就是在利用旋转惯性。
指数衰减的这个β1、β2这两个系数的作用是让它开始的时候调整的快,那快到目的地的时候,逐步的越来越慢。

最后一段,他说可以通过改变计算顺序来提高算法1的效率,具体的来说就是将循环中的最后三行,替换成最后一行的式子。
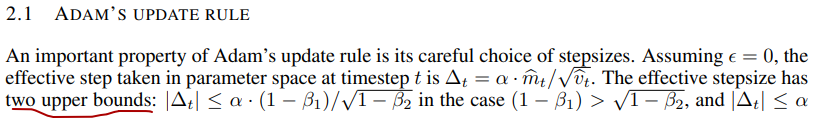
2.1这一段算是对伪代码规则的一个诠释,他说Adam的一个重要特性就是对步长的谨慎的选择,首先强调了步长的有界性(两个upper bounds)。

其次,强调在当前参数值下确定了一个置信域要优于没有提供足够信息的当前梯度估计,这正可以令其相对简单的提前知道alpha的一个正确范围,第三,他在这里提出了这样一个信噪比(SNR),说其大小决定了符合真实梯度方向的不确定性,SNR值在最优解的附近趋向于0,因此也会在参数空间有更小的有效步长,从而实现自动退火。
当Adam算法遇到鞍点的时候,随机梯度下降在鞍点附近移动产生的噪声能让当前点迅速跳出这个鞍点,另外面对一段时间梯度连续为0的平坦区域,或者说梯度稀疏的情况,Adam算法也能利用历史积累的梯度信息快速的穿过,此外当接近极小值的时候,所有方向上的噪声都会很大,从而使得信噪比接近于0,让更新步长迅速减小到0,作者将之为自动退火也就是这个意思了。
在这一段的最后作者也强调了,Adam算法它对梯度的对角缩放具备不变性,有效步长Δt对于梯度缩放来说仍然是个不变的量。
偏差修正

接下来的第三部分,是对积累梯度和梯度平方v进行了归一化修正的一种具体理论解释,概括的来说就是,
通过
i
n
i
t
i
a
l
i
z
a
t
i
o
n
b
i
a
s
c
o
r
r
e
c
t
i
o
n
归一化的修正可以将
m
t
和
v
t
这一阶矩、二阶矩放大,使得
t
很小的时候
m
t
^
和
v
t
^
跟
t
很大时的梯度
经过从分的累积之后的
m
t
^
和
v
t
^
的大小能够在同一水平
通过initialization bias correction归一化的修正可以将m_t和v_t这一阶矩、二阶矩放大,使得t很小的时候\hat{m_t}和\hat{v_t}跟t很大时的梯度\\ 经过从分的累积之后的\hat{m_t}和\hat{v_t}的大小能够在同一水平
通过initializationbiascorrection归一化的修正可以将mt和vt这一阶矩、二阶矩放大,使得t很小的时候mt^和vt^跟t很大时的梯度经过从分的累积之后的mt^和vt^的大小能够在同一水平
具体的来说公式1是一个指数加权平均数的完全展开式,公式2就是为了让指数指数加权平均数v_t和真实值g_t平方更加接近,求期望,看两者之间的差别。在下面指出了指数加权平均数的偏差修正公式的由来。
收敛性理论证明

第四部分主要用在线学习框架分析了Adam算法的收敛性。
相关算法

第五部分主要讲了和其它文献其它算法的相关性,梯度下降算法经历了一个发展的历程,首先是从SGD随机梯度下降算法开始,然后发展出了RMSProp、AdaGrad还有改进的AdaDelta等等,这样的很多种的梯度下降算法,本文重点比较了AdaGrad和RMSProp这两种算法,因为是在这两个算法的基础上发展出来的Adam算法,把他们两者的优点结合到了一起,作者为了区分具体的分析了Adam和这两种算法的不同。

先来看看AdaGrad(自适应梯度算法),它是让不同的参数有不同的学习率,增加了衰减项,提供了稀疏梯度问题的性能,比方说在NLP和视觉领域里边,大量的问题都是梯度都是稀疏梯度的这种情况,对于RMSProp,实际上是均方根传播,它也是维护了每个参数的学习率,但根据最近的权重梯度平均值来调整。
Adam算法把两者的优点结合到了一起,不同的参数有自己的学习率,而且还有自己的动量,也就是说更加的个性化,因此每个参数更加独立,提升了模型的训练速度和稳定性。
从区别上来讲,RMSProp算法和Adam算法相比,它在带动量计算时重新计算梯度上的动量,而不是指数加权平均数的算法,没有偏差修正,AdaGrad算法与Adam算法相比,前者参数更新是没有β的,有偏差修正。
实验

第六部分是实验结果,从report的数据来看,作者分别用逻辑回归加上MNIST、多层神经网络加上MNIST、卷积神经网络加上CIFAR10进行了实验,将Adam算法与其它优化算法进行了详细的对比,实验的细节写的非常清楚。
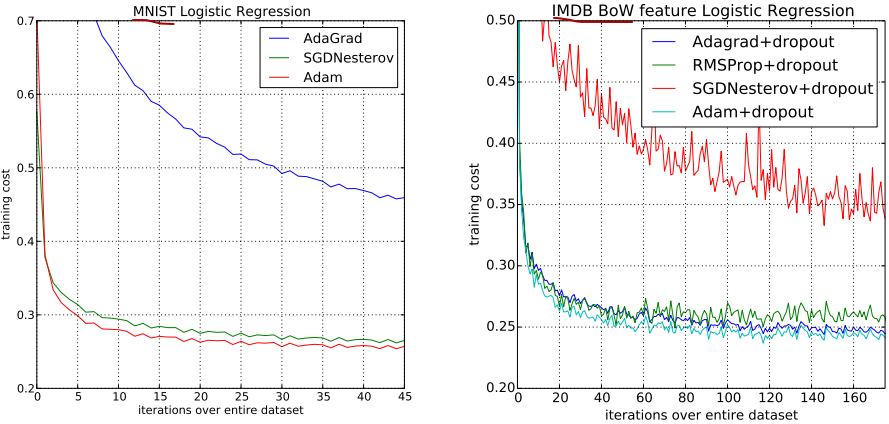

先看逻辑回归的这个图,逻辑回归是标准的凸函数,因此在优化时不需要担心局部最优解的问题,第一个对比是在MNIST上计算时采用了一个衰减,我们可以看到Adam在收敛域上和SGDN算法这两条线比较接近,快于AdaGrad。
第二组对比是在IMDB movie review这个数据集上,由于数据本身就是特别稀疏的,可以看到SGDN的表现不是很好,相对于Adam来说,无论是Adam还是RMSProp还是AdaGrad,他们都比这个SGDN强不少。
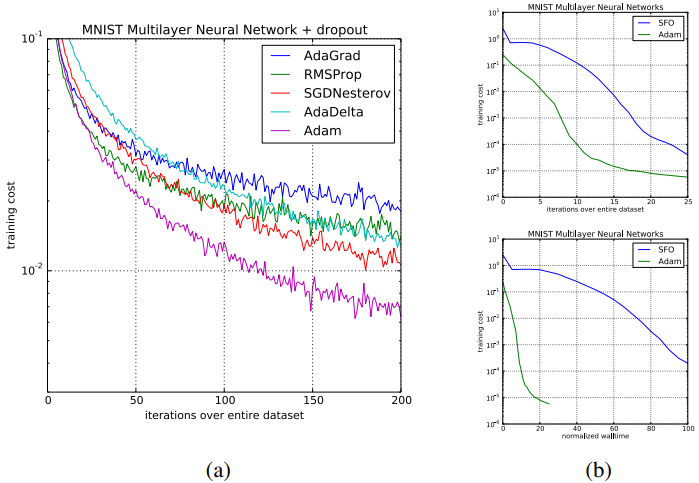

再来看一下图二,这个是对常用的多层神经网络的一个实验,由于通常这种网络用来拟合非凸函数,因此可以测试Adam优化器不受局部最优解限制的能力,实验结果上来看,在MNIST images上,Adam在收敛速率以及最小化损失函数上,都比其它的优化器要出色不少。
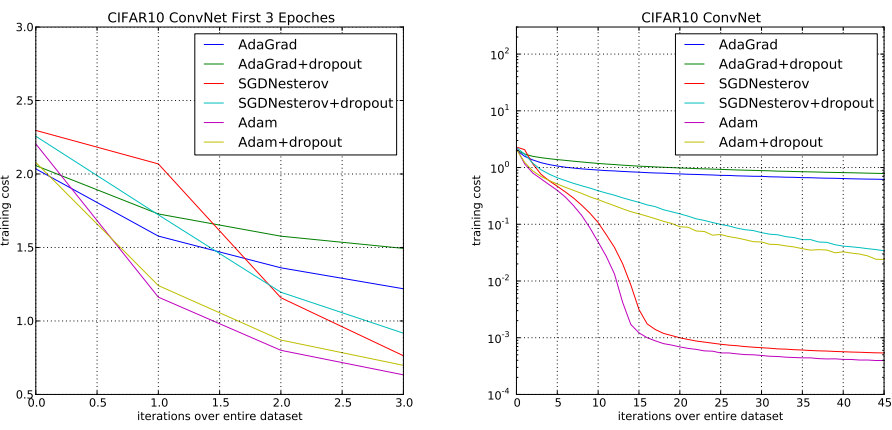
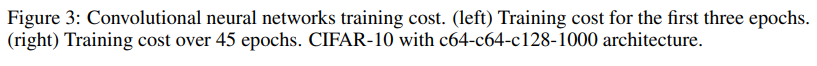
接下来的测试都是更加复杂的卷积神经网络,来看图三,这个主要是来测试Adam是否能够针对不同的model都取得不错的优化结果,这次是在CIFAR10数据集上,Adam任然取得了最好的一个结果。
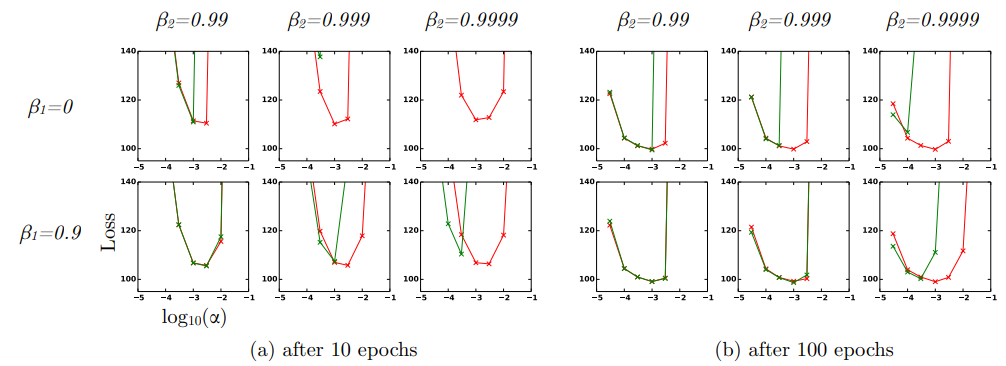

图四测试了偏差矫正项对于结果的影响,图中绿线为移除bias term的结果,红线为保留bias term偏差项的结果,由于移除bias term之后,Adam的算法也是比较接近于RMSProp,因此可以得出Adam的优化能力不弱于RMPSrop,具体执行的是2013年的这篇paper里面的VAE模型
ADAMAX

第七部分主要讲解了,Adam的一个变体Adamax,也是很多数学的分析。和Adam相比,唯一变动的就是红圈的地方,mt有偏差修正,反倒是vt不见了,改成了ut。
结论

除了简单的总结之外,作者还提出了下一步研究的方向主要是Adam超参数的设置,同时也指出了一些缺点的改进,Adam虽然收敛的很快很稳定,但是收敛的时候是有些差的,即收敛到它的最优解的准确率要偏低一点,因此也有一些更好的优化算法后来对Adam进行一些改进。
























 905
905











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










