第十一章 曲线积分与曲面积分

已于 2023-07-08 11:09:41 修改
阅读量1k 收藏 15
点赞数 9
分类专栏： 根据宋浩老师的网课《高等数学》整理的笔记 文章标签： matlab 笔记
于 2023-06-07 18:11:45 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/m0_60146935/article/details/131093190
版权

目录


说明：为了复习高数，该文章是学习课程 《高等数学》同济版 全程教学视频（宋浩老师）而记录的笔记，笔记、MATLAB代码来源于本人。若有侵权，请联系本人删除。笔记难免可能出现错误或笔误，若读者发现笔记有错误，欢迎在评论里批评指正。参考书籍： 高等数学下册(同济_第7版)。

一、对弧长的曲线积分

1.1 对弧长曲线积分的概念与性质（引例(求曲线构件的质量)、定义、性质）

在这里插入图片描述

1.2 对弧长的曲线积分的计算法（参数方程下的曲线积分）

在这里插入图片描述
例1的代码：

clc;
clear ;
close all;
x = linspace(0,1,20);
y = x.^2;
figure;
plot(x,y)
xlabel('x');
ylabel('y');
title('曲线L：y=x^2在O与B之间的曲线');
text(0-0.06,0-0.02,'点O','HorizontalAlignment','center')
text(1+0.01,1+0.01,'点B','HorizontalAlignment','center')

例2的代码：

clc;
clear ;
close all;
% 1.基本图形
R = 2;
alpha_0 = -35:0.2:35;
alpha = alpha_0/180*pi;
x = R*cos(alpha);
y = R*sin(alpha);
figure;
plot(x,y);
hold on;
x1 = linspace(0,R*cos(alpha(end)),50);
y1 = x1*tan(alpha(end));
y2 = -x1*tan(alpha(end));
plot(x1,y1,'--');plot(x1,y2,'--');
xlabel('x');
ylabel('y');
title('半径为R、中心角为2α的圆弧L');

% 2.x轴与y轴
% 2.1 x轴
% ------------x 轴参数(注意理解)------------------
axis([0 2 -2 2]);
p1=[0 0];p2=[2.1 0];%从点（0，0）到（2.1，0）,根据需要进行调整
%坐标转换，将点p1、p2实际axes坐标转成figure坐标
% 获取 Axes 位置
posAxes = get(gca, 'Position');
posX = posAxes(1);
posY = posAxes(2);
width = posAxes(3);
height = posAxes(4);
% 获取 Axes 范围
limX = get(gca, 'Xlim');
limY = get(gca, 'Ylim');
minX = limX(1);
maxX = limX(2);
minY = limY(1);
maxY = limY(2);
% 转换坐标
xNew1 = posX + (p1(1) - minX) / (maxX - minX) * width;
xNew2 = posX + (p2(1) - minX) / (maxX - minX) * width;
yNew1 = posY + (p1(2) - minY) / (maxY - minY) * height;
yNew2 = posY + (p2(2) - minY) / (maxY - minY) * height;
% -------------画x轴----------------------------
annotation(gcf, 'arrow', [xNew1 xNew2], [yNew1 yNew2]);
annotation(gcf, 'textbox',[xNew2 yNew2 0 0], 'String', 'x', 'EdgeColor', 'none');
% 2.2 y轴
p1=[0 -2.2];p2=[0 2.2];%从点（0，-2.2）到（0，2.2）,根据需要进行调整
%坐标转换，将点p1、p2实际axes坐标转成figure坐标
% 获取 Axes 位置
posAxes = get(gca, 'Position');
posX = posAxes(1);
posY = posAxes(2);
width = posAxes(3);
height = posAxes(4);
% 获取 Axes 范围
limX = get(gca, 'Xlim');
limY = get(gca, 'Ylim');
minX = limX(1);
maxX = limX(2);
minY = limY(1);
maxY = limY(2);
% 转换坐标
xNew1 = posX + (p1(1) - minX) / (maxX - minX) * width;
xNew2 = posX + (p2(1) - minX) / (maxX - minX) * width;
yNew1 = posY + (p1(2) - minY) / (maxY - minY) * height;
yNew2 = posY + (p2(2) - minY) / (maxY - minY) * height;
% -------------画y轴----------------------------
annotation(gcf, 'arrow', [xNew1 xNew2], [yNew1 yNew2]);
annotation(gcf, 'textbox',[xNew2 yNew2 0 0], 'String', 'y', 'EdgeColor', 'none');

hold off;

二、对坐标的曲线积分

2.1 对坐标的曲线积分的概念与性质（引例(变力沿曲线所作的功)、定义、性质）

在这里插入图片描述
例3的代码：

clc;
clear ;
close all;
a = 2;k = 3;
t = linspace(0,2*pi,100);
x = a*cos(t);
y = a*sin(t);
z = k*t;
figure;
plot3(x,y,z);
hold on;
xlabel('x');
ylabel('y');
zlabel('z');
title('弧Γ');
grid on;
hold off;

在这里插入图片描述

2.2 对坐标的曲线积分的计算法（参数方程下的曲线积分、两类曲线积分的区分）

在这里插入图片描述
在这里插入图片描述
例1的代码：

clc;
clear ;
close all;
% 1.绘制 y^2=x 曲线
x = 0:0.01:1.4;
y1 = sqrt(x);
y2 = -sqrt(x);
figure;
plot(x,y1,'color',[1 0.5 0]);% 橙色线
hold on; % 保留绘图
plot(x,y2,'color',[1 0.5 0]);
xlabel('x');
ylabel('y');
title('y^2=x');
% 2.在点 A 和点 B 上进行标注
O = [1, -1];
A = [1, 1];
plot(O(1), O(2), 'bo','LineWidth',1.5); % 在点A处画出一个蓝色圆点
text(O(1)+0.05, O(2)+0.1, 'A'); % 在点A处写上文字"A"
plot(A(1), A(2), 'bo','LineWidth',1.5); % 在点 B 处画出一个蓝色圆点
text(A(1)+0.05, A(2)+0.15, 'B'); % 在点B处写上文字"B"
hold off;

例2的代码：

clc;
clear ;
close all;
% 1.绘制(1)的L
theta = linspace(0,pi,50);
a = 2;
x1 = 2*cos(theta);
y1 = 2*sin(theta);
figure;
plot(x1,y1,'color',[1 0.5 0],'LineWidth',1.5);% 橙色线
hold on; % 保留绘图
xlabel('x');
ylabel('y');
% 2.绘制(2)的L
x2 = x1;
y2 = zeros(size(x2));
plot(x2,y2,'color','b','LineWidth',1.5);% 蓝色线
legend('例2.(1)的L','例2.(2)的L');
% 3.在点 A 和点 B 上进行标注
O = [a, 0];
A = [-a, 0];
plot(O(1), O(2), 'bo','LineWidth',1.5); % 在点A处画出一个蓝色圆点
text(O(1)+0.05, O(2)+0.05, 'A','Color','b'); % 在点A处写上文字"A"
plot(A(1), A(2), 'o','Color',[1 0.5 0],'LineWidth',1.5); % 在点 B 处画出一个橙色圆点
text(A(1)+0.05, A(2)+0.05, 'B','Color',[1 0.5 0]); % 在点B处写上文字"B"
axis([-2.2 2.2 0 2.2]);
title('有向线段L');
hold off;

例3的代码：

clc;
clear ;
close all;

% 1.绘制(1)的L:  抛物线y=x^2上从O(0,0)到B(1,1)的一段弧
x1 = -0.1:0.02:1.2;
y1 = x1.^2;
figure;
plot(x1,y1,'color',[1 0.5 0],'LineWidth',1.5);% 橙色线
hold on; % 保留绘图
xlabel('x');
ylabel('y');

% 3.绘制(2)的L:  抛物线x=y^2上从O(0,0)到B(1,1)的一段弧
y2 = -0.1:0.02:1.2;
x2 = y2.^2;
plot(x2,y2,'color','b','LineWidth',1.5);% 蓝线

% 3.绘制(3)的L:  有向折线OAB,这里О 、A、B依次是点(0,0)、(1,0)、(1,1)
x3 = 0:0.01:1;
y3 = 0*ones(size(x3));
x4 = linspace(1,1,50);
y4 = linspace(0,1,length(x4));
plot(x3,y3,'color','r','LineWidth',1.5);
plot(x4,y4,'color','r','LineWidth',1.5);
legend('例3.(1)的L','例3.(2)的L','例3.(3)的L');

% 4.在点O、A、B上进行标注
O = [0,0];
A = [1,0];
B = [1,1];
plot(O(1), O(2), 'bo','LineWidth',1.5); % 在点O处画出一个蓝色圆点
text(O(1)-0.1, O(2)-0.1, 'O','Color','b','FontSize',18); % 在点O处写上文字"O"
plot(A(1), A(2), 'o','Color',[1 0.5 0],'LineWidth',1.5); % 在点 A 处画出一个橙色圆点
text(A(1)+0.05, A(2)+0.05, 'A','Color',[1 0.5 0],'FontSize',18); % 在点B处写上文字"A"
plot(B(1), B(2), 'o','Color','r','LineWidth',1.5); % 在点 B 处画出一个橙色圆点
text(B(1)+0.05, B(2)-0.05, 'B','Color','r','FontSize',18); % 在点B处写上文字"B"
title('有向线段L');
axis([-0.2 1.5 -0.2 1.5]);

% 5.x轴与y轴
% 5.1 x轴
% ------------x 轴参数(注意理解)------------------
p1=[-0.2 0];p2=[1.5 0];%从点p1到p2,根据需要进行调整
%坐标转换，将点p1、p2实际axes坐标转成figure坐标
% 获取 Axes 位置
posAxes = get(gca, 'Position');
posX = posAxes(1);
posY = posAxes(2);
width = posAxes(3);
height = posAxes(4);
% 获取 Axes 范围
limX = get(gca, 'Xlim');
limY = get(gca, 'Ylim');
minX = limX(1);
maxX = limX(2);
minY = limY(1);
maxY = limY(2);
% 转换坐标
xNew1 = posX + (p1(1) - minX) / (maxX - minX) * width;
xNew2 = posX + (p2(1) - minX) / (maxX - minX) * width;
yNew1 = posY + (p1(2) - minY) / (maxY - minY) * height;
yNew2 = posY + (p2(2) - minY) / (maxY - minY) * height;
% -------------画x轴----------------------------
annotation(gcf, 'arrow', [xNew1 xNew2], [yNew1 yNew2]);
annotation(gcf, 'textbox',[xNew2 yNew2 0 0], 'String', 'x', 'EdgeColor', 'none');
% 5.2 y轴
p1=[0 -0.2];p2=[0 1.5];%从点p1到p2,根据需要进行调整
%坐标转换，将点p1、p2实际axes坐标转成figure坐标
% 获取 Axes 位置
posAxes = get(gca, 'Position');
posX = posAxes(1);
posY = posAxes(2);
width = posAxes(3);
height = posAxes(4);
% 获取 Axes 范围
limX = get(gca, 'Xlim');
limY = get(gca, 'Ylim');
minX = limX(1);
maxX = limX(2);
minY = limY(1);
maxY = limY(2);
% 转换坐标
xNew1 = posX + (p1(1) - minX) / (maxX - minX) * width;
xNew2 = posX + (p2(1) - minX) / (maxX - minX) * width;
yNew1 = posY + (p1(2) - minY) / (maxY - minY) * height;
yNew2 = posY + (p2(2) - minY) / (maxY - minY) * height;
% -------------画y轴----------------------------
annotation(gcf, 'arrow', [xNew1 xNew2], [yNew1 yNew2]);
annotation(gcf, 'textbox',[xNew2 yNew2 0 0], 'String', 'y', 'EdgeColor', 'none');

hold off;

三、两类曲线积分的联系（两种证明联系的方法）

在这里插入图片描述

四、格林公式及其应用

4.1 格林公式的定义和证明（引述、平面单连通区域的概念、边界曲线的正方向、格林公式的定义及证明）

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

4.2 格林公式的计算

在这里插入图片描述

4.3 平面上曲线积分与路径无关的概念、条件

在这里插入图片描述

五、对面积的曲面积分

5.1 对面积的曲面积分的概念与性质（回顾、曲线积分的分类、曲面积分的分类、引例(求曲面构件的质量)、定义、曲面面积的求法、性质(积分的存在性、积分区域的可加性、线性、不等式关系)）

在这里插入图片描述

5.2 对面积的曲面积分的计算法（计算步骤（“一投二代三微变”）、投影面的一般选取规则、利用性质简化运算（奇偶性、轮换对称性、有的题可用质心公式进行简化））

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

六、对坐标的曲面积分

6.1 有向曲面的定义、分类、方向及曲面元素的投影

在这里插入图片描述
例6的代码：

clc;
clear ;
close all; 
% 1.Σ的参数方程
n = 50;
theta = linspace(0,2*pi,n);
phi = linspace(0,pi,n/2);
[theta,phi] = meshgrid(theta,phi);
x = sqrt(3)*sin(phi).*cos(theta)+1;
y = sqrt(3)*sin(phi).*sin(theta)+1;
z = sqrt(3)*cos(phi)+1;
% 2.画图
figure;
mesh(x,y,z);
hold on;
xlabel('x');
ylabel('y');
zlabel('z');
title('曲面Σ');
grid on;
axis tight;
hidden off %打开透视
hold off;

6.2 对坐标的曲面积分的概念与性质（定义、性质）

在这里插入图片描述

6.3 对坐标的曲面积分的计算法（步骤（“一投二代三定号”）、利用性质简化计算（奇偶性、轮换对称性））

在这里插入图片描述
在这里插入图片描述
例2的代码：

clc;
clear ;
close all; 
% 1.Σ的参数方程
n = 50;
theta = linspace(0,1/2*pi,n);
phi = linspace(0,pi,n/2);
[theta,phi] = meshgrid(theta,phi);
x = 1*sin(phi).*cos(theta);
y = 1*sin(phi).*sin(theta);
z = 1*cos(phi);
% 2.画图
figure;
mesh(x,y,z);
hold on;
xlabel('x');
ylabel('y');
zlabel('z');
title('曲面Σ');
grid on;
axis tight;
hidden off %打开透视
hold off;

6.4 两类曲面积分的联系

在这里插入图片描述
在这里插入图片描述
例6的代码：

clc;
clear ;
close all;
% 1.曲面Σ的参数方程
theta = linspace(0,2*pi,60);
z = linspace(0,2,80);
[theta,z]=meshgrid(theta,z);
x = sqrt(2*z).*cos(theta);
y = sqrt(2*z).*sin(theta);
% 2.画图
figure;
mesh(x,y,z);
hold on;
xlabel('x');
ylabel('y');
zlabel('z');
title('曲面Σ');
grid on;
axis tight;
hidden off %打开透视
hold off;

在这里插入图片描述
在这里插入图片描述

七、高斯公式、通量与散度

7.1 高斯公式（与格林公式的关系、定义）

在这里插入图片描述

7.2 沿任意闭曲面积分的曲面积分为零的条件

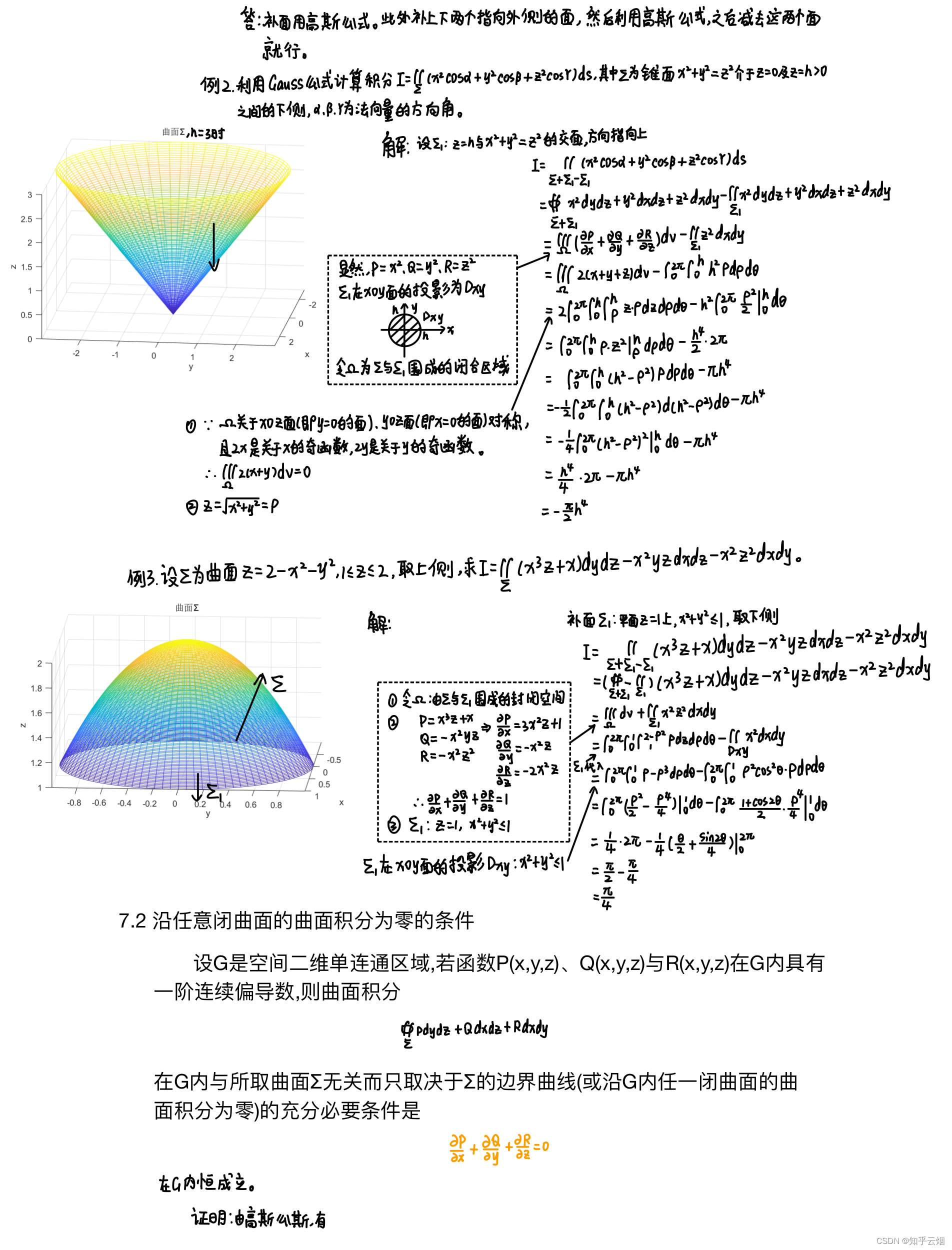
在这里插入图片描述
例2的代码：

clc;
clear ;
close all;
% 1.曲面Σ的参数方程
h = 3;
theta = linspace(0,2*pi,60);
z = linspace(0,h,80);
[theta,z]=meshgrid(theta,z);
x = sqrt(z.^2).*cos(theta);
y = sqrt(z.^2).*sin(theta);
% 2.画图
figure;
mesh(x,y,z);
hold on;
xlabel('x');
ylabel('y');
zlabel('z');
title('曲面Σ');
grid on;
axis tight;
hidden off %打开透视
hold off;

例3的代码：

clc;
clear ;
close all;
% 1.曲面Σ的参数方程
theta = linspace(0,2*pi,100);
z = linspace(1,2,100);
[theta,z]=meshgrid(theta,z);
x = sqrt(2-z).*cos(theta);
y = sqrt(2-z).*sin(theta);
% 2.画图
figure;
mesh(x,y,z);
hold on;
xlabel('x');
ylabel('y');
zlabel('z');
title('曲面Σ');
grid on;
axis tight;
axis equal;
hidden off %打开透视
hold off;

7.3 通量、散度、无源场

在这里插入图片描述
例5的代码：

clc;
clear ;
close all;
% 1.曲面Σ的参数方程
theta = linspace(0,pi,50);
x = linspace(0,1,100);
[theta,x]=meshgrid(theta,x);
y = 1.*cos(theta);
z = 1.*sin(theta);
% 2.画图
figure;
mesh(x,y,z);
hold on;
xlabel('x');
ylabel('y');
zlabel('z');
title('曲面Σ');
grid on;
axis tight;
axis equal;
hidden off %打开透视
hold off;

八、斯托克斯公式、环流量与旋度

8.1 斯托克斯公式（与格林公式的关系、定义、证明）

在这里插入图片描述

8.2 空间曲线积分与路径无关的条件

在这里插入图片描述

8.3 环流量与旋度（环流量的定义、旋度的定义、几个符号的区分（哈密顿算子、梯度、散度、旋度、拉普拉斯算子）、无旋场与调和场、环流量与旋度的关系式）

在这里插入图片描述
在这里插入图片描述

曲线积分与曲面积分
zwz_chome的博客
06-17 1万+
曲线积分与曲面积分 首先，一定要明确不同的东西，使用不同的积分。
曲线积分与曲面积分总结_第一类曲线，曲面积分
weixin_39614528的博客
11-21 1703
所谓第一类积分就是普通的长度面积体积的积分第一类曲线积分:思考：积分原理都大同小异，大家有兴趣可以思考一下，三维中两个面联立得到的一般曲线方程，如何计算长度？第一类曲面积分：具体就是积分空间曲面面积，如果含有被积函数f（x，y，z）就相当于：曲面每一个点有了对应的密度，然后计算质量。计算方法：总结来说：就是被积函数将z换为（x，y）表示，及面积dS= Dxy三维曲面投影到xOy面积区域这样就将一...
曲线积分与曲面积分（微积分）
xxayt的博客
06-07 2078
1 第一型曲线积分（对弧长） 一、概念 讨论非均匀的曲线形构件的质量 P89 定义1： ∫Lf(x,y) ds=lim⁡λ→0∑i=1nf(xi,yi)Δsi\int_Lf(x,y)\,ds=\lim\limits_{\lambda\rightarrow 0}\sum\limits_{i = 1}^n f(x_i,y_i)\Delta s_i∫L​f(x,y)ds=λ→0lim​i=1∑n​f(xi​,yi​)Δsi​，其中λ=max⁡1≤i≤n{Δsi}\lambda=\max\limits_{1\
高等数学-曲线积分与曲面积分
linkequa的博客
10-25 8944
1，第一类曲线积分（对弧长的曲线积分） 1.1 定义 1.2 计算方法 2，第二类曲线积分（对坐标的曲线积分） 2.1 定义 2.2 计算方法 3，两类曲线积分之间的关系 4，格林公式 格林公式解决的问题：在平面闭区域D上的二重积分可以通过沿闭区域D的边界曲线L上的曲线积分来表示。 5，平面上曲线积分与路径无关的条件 6，第一类曲面积分（对面积的曲面积分） 6.1 定义 6.2 ...
高数(下) Ch11.曲线积分与曲面积分
Edward2022的博客
10-06 1万+
线面积分
高等数学第五版下册第十一章曲线积分与曲面积分复习知识点及例题.pdf
10-14
高等数学曲线积分与曲面积分知识点总结 曲线积分是高等数学中一个重要的概念，它广泛应用于物理、工程、经济等领域。曲线积分可以分为两类：对弧长的曲线积分（第一类）和对坐标的曲线积分（第二类）。 对弧长的...
整理高等数学第五版下册第十一章曲线积分与曲面积分复习知识点及例题.pdf
09-12
整理高等数学第五版下册第十一章曲线积分与曲面积分复习知识点及例题.pdf
第十一章-曲线积分与曲面积分--答案.doc
最新发布
06-25
【曲线积分与曲面积分】是微积分学中的高级概念，主要应用于研究和计算复杂的几何形状和物理问题。这部分内容通常出现在高等数学的多元函数微积分课程中。 **一、曲线积分** 曲线积分分为两类：对向量场的线积分和...
数学分析笔记17：曲线积分与曲面积分
小辉的数学博客
03-27 4144
内容摘要：1.第一型曲线/曲面积分的定义与计算 2.第二型曲线/曲面积分的定义与计算 3. 格林公式、高斯公式、斯托克斯公式 4. 积分与路径无关
曲线积分与曲面积分解题技巧
01-17
最近刚看到的好资源，快来下啊！！！！！！！！
第11章 曲线积分与曲面积分
jinesse
09-06 2688
第一节 对弧长的曲线积分第二节 对坐标的曲线积分第三节 格林公式及其应用第四节 对面积的曲面积分第五节 对坐标的曲面积分第六节 高斯公式 通量与散度第七节 斯托克斯公式 环流量与旋度
曲线积分与曲面积分总结_曲线积分和曲面积分公式总结
weixin_39880328的博客
11-21 994
这是我第一次写文章，还是有点兴奋。 ️内容是自己看完曲线积分和曲面积分后的公式总结。本人正在准备考研，希望可以通过写文章的方式督促自己多总结，也可以将自己的学习成果和大家分享。文中难免有错的地方，希望大家见谅。后面还会有更新哦 ————————————————————重新写了一下，这次比较清楚了...
九章曲线积分与曲面积分
fgh123的博客
09-13 1987
文章目录1 梯度定义7.12 散度为讨论流体速度场$\pmb{v}(M)$在曲面$\Sigma$内某一点$M_0$的流量令闭曲面缩向定点$M_0$向量场的散度概念 1 梯度 定义7.1 设3维空间区域GGG定义一个数量函数f(x,y,z)f(x,y,z)f(x,y,z) 则f(x,y,z)f(x,y,z)f(x,y,z)构成个数量场 点P(x,y,z)∈GP(x,y,z)\in GP(x,y,z...
曲面积分与曲线积分
m0_53210180的博客
03-23 6859
​​​​​​​。
微积分之曲线积分与曲面积分超详细知识框架
凝望，划过星空的博客
06-07 9320
微积分之曲线积分与曲面积分超详细知识框架 这个是我在学完了这一章的时候画的，我个人觉得吧，大家千万不要以为制作思维导图花费时间，其实你在做思维框架的时候，是对整个这一章所有知识的一种大局观，我们能够在这个过程中清楚知识之间的联系，能够让我们的知识更加系统，思维更加富有逻辑 下面是第九章的思维导图，仅供大家自己学习使用 ...
【高等数学笔记】两类曲线积分、曲面积分的转化
热门推荐
qaqwqaqwq的博客
05-24 1万+
整体思想：局部均匀化，用很小的长度/面积元上一点某个量的数值来代替整个元的数值。 # 一、曲线积分 ## （一）弧长的计算公式 设曲线$\Gamma$的参数方程为$x=x(t),y=y(t),z=z(t)$。令$\bm r=(x,y,z)$，则方程为$\bm r=\bm r(t)$。
同济版高等数学第十一章：曲线与曲面积分解析
标题中提到的“高等数学第十一章同济版”指的是中国高等教育出版社出版的《高等数学》教材中的一章。由于具体版本未明确给出，这里假定它是以同济大学数学系编写的《高等数学》第六版为参照，该教材在中国大学中广泛...
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

知乎云烟

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值