三维重建（3）--单视几何

Struart_R

已于 2024-01-19 23:03:16 修改

阅读量1k

点赞数 23

分类专栏：三维重建文章标签：计算机视觉三维重建人工智能

于 2024-01-19 23:02:59 首次发布

本文链接：https://blog.csdn.net/m0_60177079/article/details/135706461

版权

三维重建专栏收录该内容

8 篇文章 2 订阅

订阅专栏

一、无穷远点、无穷远线、无穷远平面

对于下面所有的坐标均用齐次坐标表述，而不是欧式坐标

1、2D平面上的无穷远问题

（1）2D平面上的线

对于一条2D平面上的直线，我们可以用 $ax_1+bx_2+c=0$ 来表示，其中参数可以单独拿出来，作为一个整体，一个参数向量的形式（后续将沿用这种方法来表示一条线），即下面的 $\mathbf{\mathit{l}}=[a \hspace{0.25cm} b \hspace{0.25cm} c]^T$ ，x作为直线上的一个点表示为 $x=[x_1,x_2,1]^T$ ，这也满足了 $x^Tl=0$ ，后续对于直线上的点与直线的关系均满足 $x^Tl=0$ 条件。

（2）2D平面上线的交点

定义两条直线叉乘得到的积，表示交点的坐标。如何证明2D平面上两条线的交点，交点与每一条直线间一定满足 $x^Tl=0$ 关系，那么与点乘相同，可以证明一个被定义为 $x=l \times l'$ 的点与两条直线分别垂直（点乘等于0），则他一定同时在两条线上，即相交。

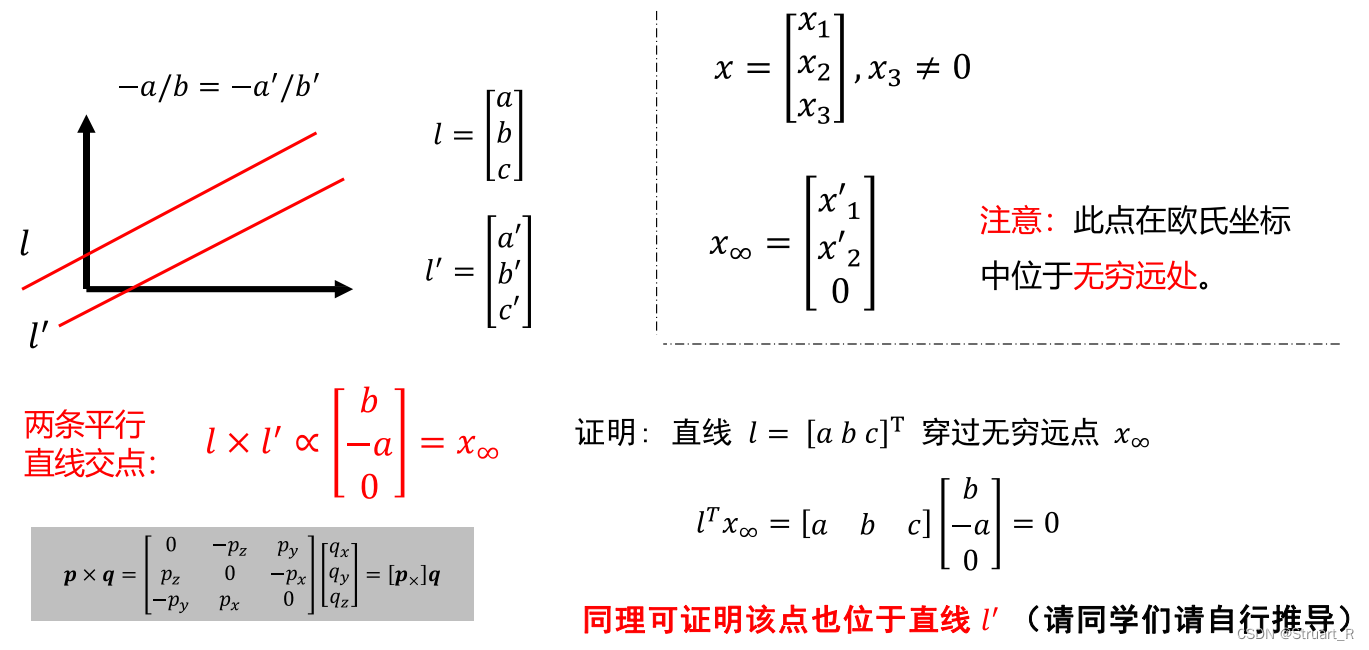
（3） 2D平面上的无穷远点

首先任意选取两条直线 $l,l'$ ，s.t. $a/b=a'/b'$ ，即斜率相同两条线平行，那么若存在两条平行直线的交点 $x_\infty$ ，则一定满足 $x_\infty =l \times l'$ ，且 $x_\infty \propto [b \hspace{0.15cm} -\hspace{0cm} a \hspace{0.25cm} 0]^T$ ，我们也可以反过来证明两条直线的任意一条均穿过无穷远点，只需要满足 $l^Tx_\infty =0$ ，对于2D平面上广义的无穷远点可以定义为 $x_\infty=[1,1,0]^T$ （后续无穷远点变换会用到）。

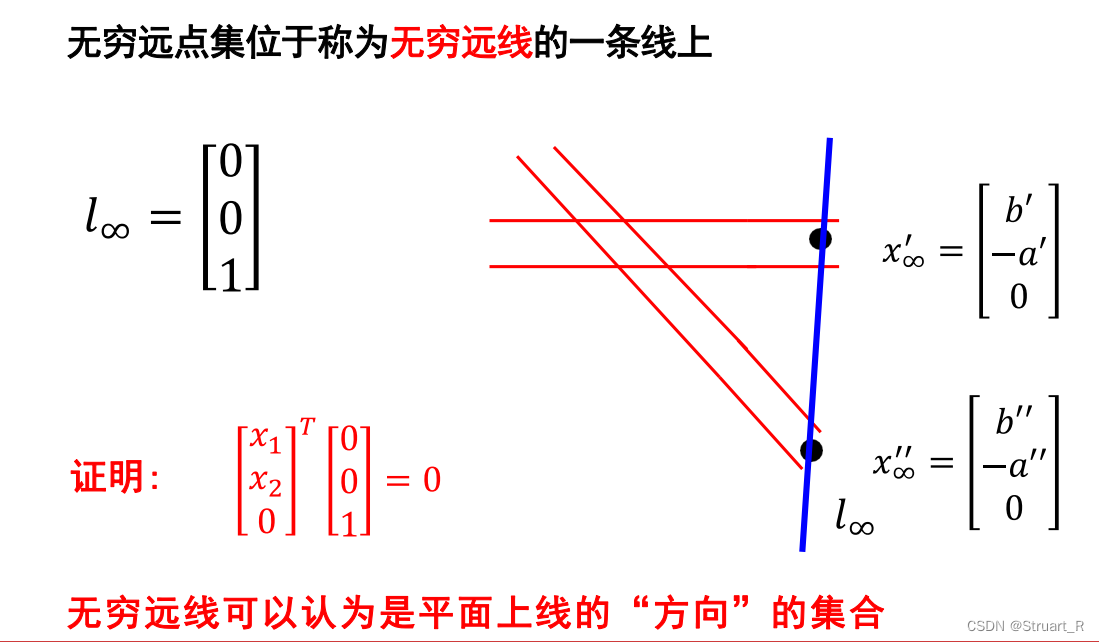
（4）2D平面上的无穷远线

同一平面（在2D平面上均为同一平面）的无穷远点均位于同一无穷远线上，我们定义无穷远线为 $l_\infty=[0 \hspace{0.25cm} 0 \hspace{0.25cm} 1]^T$ ，对于任意一个无穷远点一定满足最后一个齐次坐标 $x_3$ 为0，所以对于任意一个2D平面下的无穷远点一定会在无穷远线上满足 $l_\infty ^Tx_\infty =0$ 成立。

2、3D平面上的无穷远问题

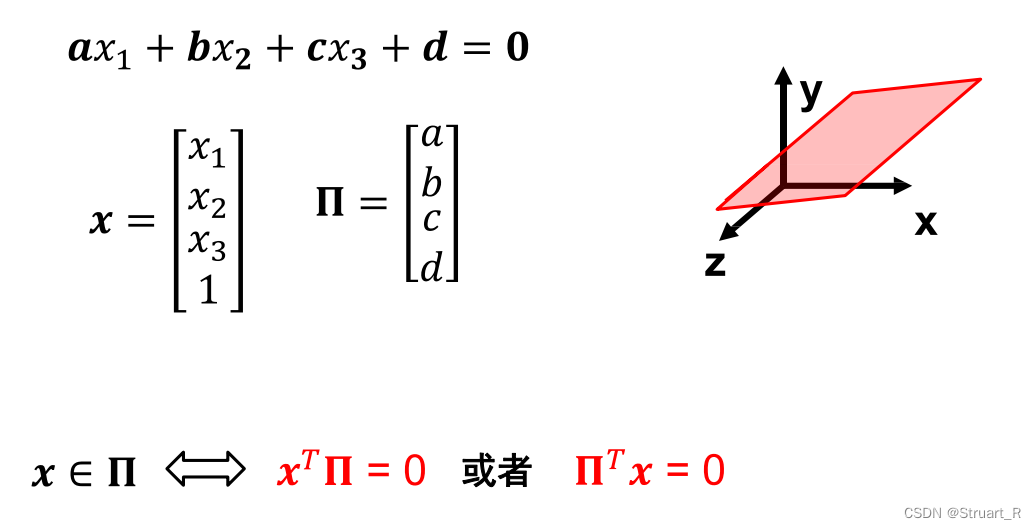
（1）3D空间中的面

对于一个3D空间中的面可以定义为 $ax_1+bx_2+cx_3+d=0$ ，同理可以将参数拆解为参数向量形式，定义参数表示的面 $\Pi = [a \hspace{0.25cm} b \hspace{0.25cm} c \hspace{0.25cm} d]$ ，对于一个面上的点 $x=[x_1,x_2,x_3,1] ^T$ ，仍然有 $x^T \Pi =0$ 成立。

（2） 3D空间中的直线

3D空间中的直线，一般很难去表示，可以用直线方向来粗略表示。

（3）3D空间中的无穷远点

3D空间中的无穷远点，定义为 $x_4$ 为0，其他三个坐标任意。此时必须保证同一平面上的平行线相交于同一无穷远点。

（4）3D空间中的无穷远线和无穷远面

对于平行平面会在无穷远处相交于同一条公共线，即无穷远直线，而若干条无穷远直线形成无穷远平面。定义无穷远平面为 $\Pi=[0,0,0,1]^T$ 。

二、影消点与影消线

1、2D平面上的无穷远点，无穷远线变换

（1）2D平面无穷远点变换

变换主要考察投影变换和仿射变换，对于2D平面上点到点的变换就是乘以一个变换矩阵的映射关系，即 $p'=Hp$ ， $H$ 表示变换矩阵，对于透视和仿射变换而言，仿射变换的无穷远点不变，透视变换的无穷远点不同。

点到点变换请参考：三维重建（2）--摄像机标定-CSDN博客

（2）2D平面线的变换

线的变换等价于任意点 $x$ 在线 $l$ 上，该点 $x$ 进行变换得到 $x'$ ，变换后的点 $x'$ 又一定在变换后的线 $l'$ 上，所以通过式子的代换得到了线与线之间变换是乘以一个变换矩阵的转置的逆的映射关系，即 $l'=H^{-T}l$ 。

（3）2D平面的无穷远线的变换

根据线到线的变换关系，可以得到对于无穷远线经过仿射变换不变，透视变换会改变。

2、影消点

影消点：三维空间中的无穷远点在图像中的投影点，在多视几何中，三维空间中两条平行线相交于无穷远点，而投影到二维空间的像平面坐标下就是一个有有意义坐标的点。

一般我们定义三维空间的平行线方向为 $d=[a,b,c]^T$ ，而三维空间中的无穷远点为 $x_\infty=[a,b,c,0]^T$ ，假设像平面的影消点为 $v$ ，那么一定有 $v=Kd$ 成立，建立起影消点与无穷远点的关系（在不考虑摄像机外参数的情况下，即 $M=K$ ）。此时d没有规定模长为1，所以进行规范化直线方向，得到 $d=\frac{K^{-1}v}{||K^{-1}v||}$ 。

3、影消线

影消线：三维空间中的无穷远线在图像中的投影线，即影消线，由于摄像机经过一个透视变换将三维空间的坐标转换为二维坐标，那么可以利用线与线的变换关系，计算出影消线与无穷远线的关系 $l_{horiz}=H^{-T}l_\infty$ 。

下图为三维空间下，同一平面的两条平行线在无穷远处相交，在像平面下形成的影消点，无数影消点形成影消线。

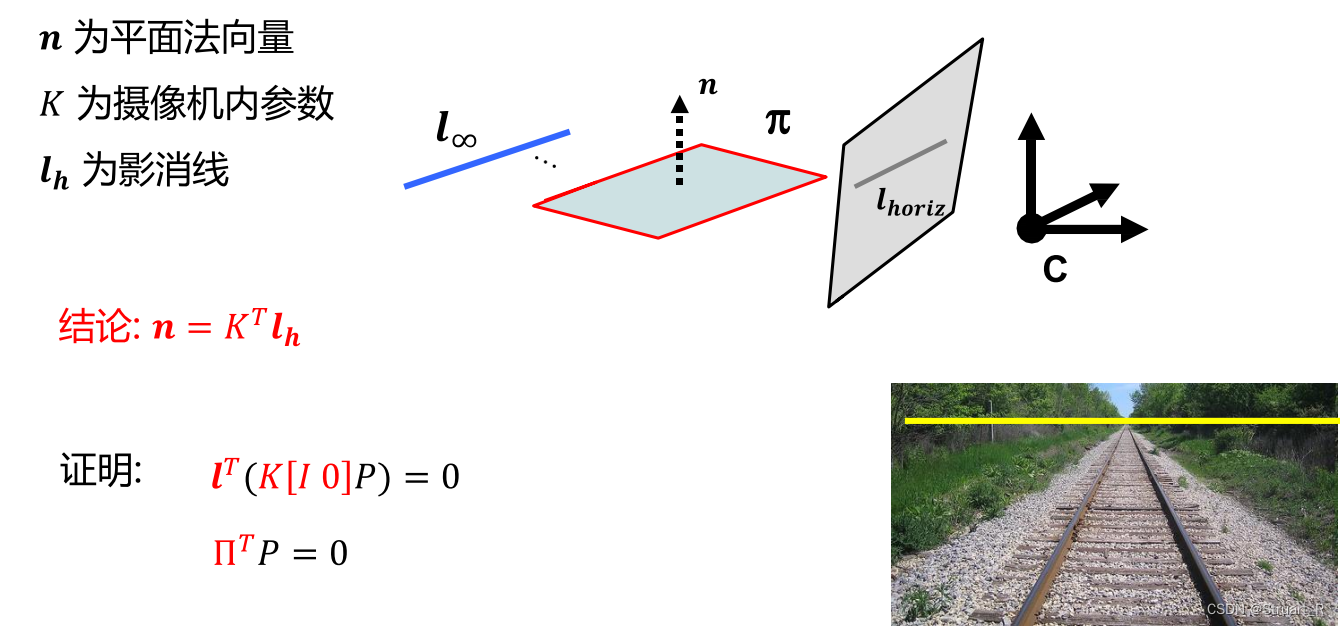
另外可以得到影消线与平面法向量的关系，我们可以知道多个平行平面会聚在无穷远处得到无穷远线，无穷远线经过投影变换到像平面得到影消线，假设一个点 $P$ 位于生成无穷远线的平行平面中的任意一个 $\Pi$ 上的一点，记平面法向量为 $n$ ，那么一定满足 $n^T P=0$ ，另外该点经过投影变换一定在影消线上，满足 $l_h ^T(K[I \hspace{0.25cm} 0]P)=0$ 成立，所以一定有 $n=K^Tl_h$ 成立。

三、单视重构

1、两平行线夹角与影消线关系

注意是一共是四条线，两组平行线之间的夹角为θ，根据余弦定理可以得到夹角与两组平行线直线方向的关系，其中定义 $\omega=(K K^T)^{-1}$ ，

$cos\theta=\frac{d_1 \cdot d_2}{|d_1||d_2|}=\frac{v_1^T \omega v_2}{\sqrt{v_1^T \omega v_1} \sqrt{v_2^T \omega v_2}}$

2、单视图标定

由于K有5个自由度，而一般我们只能找到三组互相垂直的平行线，如下图这种典型的三个平面互相垂直，在三个平面上选择三组平行线，那么最多只能得到三个方程，而三个方程不能精确的解出五个未知数，所以一般我们规定零倾斜，正方形像素，此时内参矩阵中的θ=90°，α=β，此时只剩下三个未知数 $\alpha,c_x,c_y$ ，理论上可以解出图像中的任意点，直线位置。