计算方法——三次样条插值

小纸君

于 2024-03-16 13:42:16 发布

阅读量1k

点赞数 10

分类专栏：计算方法文章标签： matlab 算法

本文链接：https://blog.csdn.net/m0_60402183/article/details/136752330

版权

计算方法专栏收录该内容

2 篇文章 0 订阅

订阅专栏

1、理论知识

1）三次样条插值的提法

给定 y ＝ $f(x)$ 的函数表（如表所示），构造函数 $s(x)$ 满足条件：
①在 $[x_i,x_{i+1}](i=0,1,...,n-1)$ 上为不超过三次的代数多项式；
② $s(x_i) = y_i (i=0,1,...,n)$ ；
③ $s(x)\epsilon C^2[a,b]$ ，其中 $a = x_0,b=x_n$ ．
其中 $s(x)$ 称为三次样条插值函数．

x	$x_0$	$x_1$	$...$	$x_n$
y ＝ $f(x)$	$y_0$	$y_1$	$...$	$y_n$

设 $s(x)$ 在点 $x_i(i=0,1,...,n)$ 处的微商为 $m_i(i=0,1,...,n)$ ，则 $s(x)$ 在每个小
区间 $[x_i,x_{i+1}]$ 上有
$s(x_i) = y_i$ $s'(x_i) = m_i$ $s(x_{i+1}) = y_{i+1}$ $s'(x_{i+1}) = m_{i+1}$

2）三次样条插值的解法思路

1）

$s(x)$ 是不超过3次的插值函数，多段的 $s(x)$ 组成了 $f(x)$

$[x_i,x_{i+1}](i=0,1,...,n-1)$ 所以总共有n-1个分段，也就是说要求解的参数有 $4(n-1)$ 个

由表的信息，我们可以列出：

条件	方程个数
函数值相等	n
函数值连续	n-2
一阶导数连续	n-2
二阶导数连续	n-2

由此还需补充两个边界条件才能凑足4(n-1)个方程去求解4(n-1)个未知数

2）边界条件

而边界条件一般有如下两种情形：
（１）已知被插值函数 $y=f(x)$ 在两个端点 $x_0$ 和 $x_n$ 处的 微商值，即给定
$f'(x_0) = m_0$ 和 $f'(x_n) = m_n$ ，相应要求 $s'(x_0) = m_0$ 和 $s'(x_n) = m_n$
（２）已知被插值函数 $y=f(x)$ 在两个端点 x０和 xn 处的二阶微商值为０，即给
定 $f''(x_0) = 0$ 和 $f''(x_n) = 0$ ，相应要求 $s''(x_0) = 0$ 和 $s''(x_n) = 0$

3）大致的推导流程

1）先根据“函数值相等”、“函数值连续”，“一阶导连续”，设：

【参考hermite插值】

2）目标——“求解 $m_i$ 的表达式"

① 化简 $h_i = x_{i+1}-x_i$ ，代入(2.41）

② 求二阶导

2.4.2直接表现的是 $[x_i,x_{i+1}]$ 中的二阶导，从中可以获取 $s''(x_i^+)$

③ 将2.4.2中的i替换为i-1，得到的是 $[x_{i-1},x_{i}]$ 中的二阶导，从中可以获取 $s''(x_i^-)$

④ 令 $s''(x_i^-) = s''(x_i^+)$ 整理得到

⑤ 令 $\alpha_i = \frac{h_{i-1}}{h_{i-1}+h_i}$ ，上式变化为

⑥ 令 $\beta_i = 3[\frac{1-\alpha_i}{h_{i-1}}(y_i-y_{i-1})+\frac{\alpha_i}{h_i}(y_{i+1}-y_i)]$

得到

⑦ 分别令 $i = 1,2,...,n-1$ 可以得到n-1个等式组成的方程组

⑧ 补充条件后，有公式

分别整理得到：

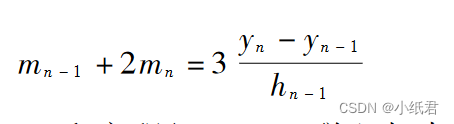
2、编程计算

1）矩阵构造

根据大致推导流程，我们需要编写函数计算如下式子：

$h_i = x_{i+1}-x_i$

$\alpha_i = \frac{h_{i-1}}{h_{i-1}+h_i}$

$\beta_i = 3[\frac{1-\alpha_i}{h_{i-1}}(y_i-y_{i-1})+\frac{\alpha_i}{h_i}(y_{i+1}-y_i)]$

def calhi(X):
  H = []
  # len(X) = n+1
  for i in range(len(X)-1):
    H.append(X[i+1]-X[i])
  return H

def calalphai(H):
  # len(H) n  0——n-1
  # 只当 A0 = 0
  A = [0]
  for i in range(1,len(H)):
    A.append((H[i-1]/(H[i-1]+H[i])))
  return A

def calbetai(A,H,Y):
  # len(A) = n 实际有效的alpha在[1:]范围内
  # Y n+1  0——n
  B = [0]
  for i in range(1,len(A)):
    tmp1 = (1-A[i])/H[i-1]*(Y[i]-Y[i-1])
    tmp2 = A[i]/H[i]*(Y[i+1]-Y[i])
    B.append(3*(tmp1+tmp2))
  return B

根据以下式子，编写函数构造矩阵

$2m_0+m_1 = \frac{3}{h_0}(y_1-y_0)$

$m_{n-1}+2m_n = 3\frac{y_n-y_{n-1}}{h_{n-1}}$

# 构造相应的矩阵
# 先构造补充条件的list
import numpy as np

def RowForSupplement(n):
  RowsFS = np.zeros(shape=(2,n+1))
  RowsFS[0][0] = 2
  RowsFS[0][1] = 1
  RowsFS[1][n-1] = 1
  RowsFS[1][n] = 2
  return RowsFS

# 构造原先的n-1个条件的方程
def Row(A):
  n = len(A)
  Rows = np.zeros(shape=(n-1,n+1))
  for i in range(1,n):
    Rows[i-1][i-1] = 1-A[i]
    Rows[i-1][i] = 2
    Rows[i-1][i+1] = A[i]
  return Rows

# 合并左侧矩阵
def Concat(Rows,RowsFS,n):
  C = np.zeros(shape=(n+1,n+1))
  C[:n-1,:] = Rows
  C[n-1:,:] = RowsFS
  return C

# 构造β矩阵
def Beta(B,Y,H):
  n = len(Y)-1
  l1 = 3*(Y[1]-Y[0])/H[0]
  l2 = 3*(Y[n]-Y[n-1])/H[n-1]
  Beta = np.zeros(shape=(n+1,))
  for i in range(1,n):
    Beta[i-1] = B[i]
  Beta[n-1] = l1
  Beta[n] = l2
  return Beta

# 解线性方程
def solve(X,Y):
  H = calhi(X)
  A = calalphai(H)
  B = calbetai(A,H,Y)
  RowsFS = RowForSupplement(len(Y)-1)
  Rows = Row(A)
  Left = Concat(Rows,RowsFS,len(Y)-1)
  beta = Beta(B,Y,H)
  M = np.linalg.solve(Left,beta)
  print(M)
  return M

2）预测函数

到solve为止，只是解出了 $m_0,m_1...m_n$ ，我们还可以编写预测函数，直接获取对于x插值函数s(x)的预测值

# 预测代码
def predict(targetX,X,Y):
  M = solve(X,Y)
  n = len(Y)
  # 确定targetX所在的区间
  st = 0
  for i in range(n-1):
    if targetX >= X[i] and targetX <= X[i+1]:
      st = i
      break
  tmp1 = (1+2*(targetX-X[st])/(X[st+1]-X[st]))*pow(((targetX-X[st+1])/(X[st]-X[st+1])),2)
  tmp2 = (1+2*(targetX-X[st+1])/(X[st]-X[st+1]))*pow(((targetX-X[st])/(X[st+1]-X[st])),2)

  tmp3 = (targetX-X[st])*pow(((targetX-X[st+1])/(X[st]-X[st+1])),2)
  tmp4 = (targetX-X[st+1])*pow(((targetX-X[st])/(X[st+1]-X[st])),2)

  return tmp1*Y[st]+tmp2*Y[st+1]+tmp3*M[st]+tmp4*M[st+1]