一、样条函数的基本原理
已知 n + 1 n+1 n+1 个数据节点,分成 n n n 个区间(Interval),在每个区间构造一个三次函数, S 0 ( x ) ∼ S n − 1 ( x ) S_0(x)\sim S_{n-1}(x) S0(x)∼Sn−1(x)。

假设每一段三次函数都用如下方程来定义:
S
i
(
x
)
=
a
i
+
b
i
(
x
−
x
i
)
+
c
i
(
x
−
x
i
)
2
+
d
i
(
x
−
x
i
)
3
,
i
=
0
,
1
,
⋯
,
n
−
1
S_i(x)=a_i+b_i(x-x_i)+c_i(x-x_i)^2+d_i(x-x_i)^3,i=0,1,\cdots,n-1
Si(x)=ai+bi(x−xi)+ci(x−xi)2+di(x−xi)3,i=0,1,⋯,n−1
那么
n
n
n 个区间对应的三次函数
S
(
x
)
S(x)
S(x) 的数学表达式如下:
S
(
x
)
=
{
S
0
(
x
)
=
a
0
+
b
0
(
x
−
x
0
)
+
c
0
(
x
−
x
0
)
2
+
d
0
(
x
−
x
0
)
3
i
f
x
0
≤
x
≤
x
1
S
1
(
x
)
=
a
1
+
b
1
(
x
−
x
1
)
+
c
1
(
x
−
x
1
)
2
+
d
1
(
x
−
x
1
)
3
i
f
x
1
≤
x
≤
x
2
⋮
S
n
−
1
(
x
)
=
a
n
−
1
+
b
n
−
1
(
x
−
x
n
−
1
)
+
c
n
−
1
(
x
−
x
n
−
1
)
2
+
d
n
−
1
(
x
−
x
n
−
1
)
3
i
f
x
n
−
1
≤
x
≤
x
n
S(x)= \begin{cases} S_0(x)=a_0+b_0(x-x_0)+c_0(x-x_0)^2+d_0(x-x_0)^3 \quad\quad\quad &if\ x_0\leq x\leq x_1\\[2ex] S_1(x)=a_1+b_1(x-x_1)+c_1(x-x_1)^2+d_1(x-x_1)^3 &if\ x_1\leq x\leq x_2\\[2ex] \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\vdots \\[2ex] S_{n-1}(x)=a_{n-1}+b_{n-1}(x-x_{n-1})+c_{n-1}(x-x_{n-1})^2+d_{n-1}(x-x_{n-1})^3 &if\ x_{n-1}\leq x\leq x_n \end{cases}
S(x)=⎩
⎨
⎧S0(x)=a0+b0(x−x0)+c0(x−x0)2+d0(x−x0)3S1(x)=a1+b1(x−x1)+c1(x−x1)2+d1(x−x1)3⋮Sn−1(x)=an−1+bn−1(x−xn−1)+cn−1(x−xn−1)2+dn−1(x−xn−1)3if x0≤x≤x1if x1≤x≤x2if xn−1≤x≤xn
每段三次函数 S ( x ) S(x) S(x) 都有 a , b , c , d a,b,c,d a,b,c,d 四个系数,上述 n n n 段三次函数,共有 4 n 4n 4n 个系数。要想求解这 4 n 4n 4n 个系数,共需要 4 n 4n 4n 个独立的方程。下面,我们根据三次样条函数对每一段三次函数在断点处的约束,生成求解 4 n 4n 4n 个系数所需要的所有方程。
条件1: n \pmb n n 段三次函数必须穿过所有已知节点
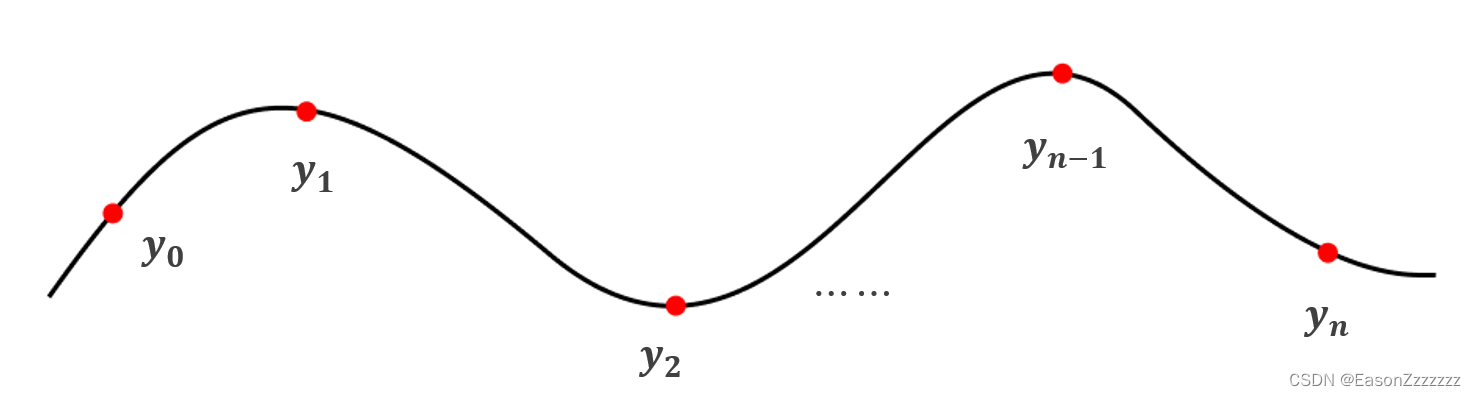
S i ( x i ) = y i , i = 0 , 1 , 2 , ⋯ , n \boxed{S_i(x_i) = y_i,\quad i=0,1,2,\cdots,n} Si(xi)=yi,i=0,1,2,⋯,n
已知
n
+
1
n+1
n+1 个节点,总共可以生成
n
+
1
n+1
n+1 个方程,即
{
y
0
=
S
0
(
x
0
)
=
a
0
+
b
0
(
x
0
−
x
0
)
+
c
0
(
x
0
−
x
0
)
2
+
d
0
(
x
0
−
x
0
)
3
=
a
0
y
1
=
S
1
(
x
1
)
=
a
1
+
b
1
(
x
1
−
x
1
)
+
c
1
(
x
1
−
x
1
)
2
+
d
1
(
x
1
−
x
1
)
3
=
a
1
⋮
y
n
−
1
=
S
n
−
1
(
x
)
=
a
n
−
1
+
b
n
−
1
(
x
n
−
1
−
x
n
−
1
)
+
c
n
−
1
(
x
n
−
1
−
x
n
−
1
)
2
+
d
n
−
1
(
x
n
−
1
−
x
n
−
1
)
3
=
a
n
−
1
y
n
=
S
n
−
1
(
x
)
=
a
n
−
1
+
b
n
−
1
(
x
n
−
x
n
−
1
)
+
c
n
−
1
(
x
n
−
x
n
−
1
)
2
+
d
n
−
1
(
x
n
−
x
n
−
1
)
3
\begin{cases} y_0=S_0(x_0)=a_0+b_0(x_0-x_0)+c_0(x_0-x_0)^2+d_0(x_0-x_0)^3=a_0\\[2ex] y_1=S_1(x_1)=a_1+b_1(x_1-x_1)+c_1(x_1-x_1)^2+d_1(x_1-x_1)^3=a_1\\[2ex] \quad\quad\quad\quad\quad\quad\quad\quad\quad\vdots\\[2ex] y_{n-1}=S_{n-1}(x)=a_{n-1}+b_{n-1}(x_{n-1}-x_{n-1})+c_{n-1}(x_{n-1}-x_{n-1})^2+d_{n-1}(x_{n-1}-x_{n-1})^3=a_{n-1}\\[2ex] y_{n}=S_{n-1}(x)=a_{n-1}+b_{n-1}(x_{n}-x_{n-1})+c_{n-1}(x_{n}-x_{n-1})^2+d_{n-1}(x_{n}-x_{n-1})^3 \end{cases}
⎩
⎨
⎧y0=S0(x0)=a0+b0(x0−x0)+c0(x0−x0)2+d0(x0−x0)3=a0y1=S1(x1)=a1+b1(x1−x1)+c1(x1−x1)2+d1(x1−x1)3=a1⋮yn−1=Sn−1(x)=an−1+bn−1(xn−1−xn−1)+cn−1(xn−1−xn−1)2+dn−1(xn−1−xn−1)3=an−1yn=Sn−1(x)=an−1+bn−1(xn−xn−1)+cn−1(xn−xn−1)2+dn−1(xn−xn−1)3
条件2:在所有节点(除了第一节点和最后一个节点)处连续
S i ( x i + 1 ) = S i + 1 ( x i + 1 ) , i = 0 , 1 , 2 , ⋯ , n − 2 \boxed{S_i(x_{i+1})=S_{i+1}(x_{i+1}),\quad i=0,1,2,\cdots,n-2} Si(xi+1)=Si+1(xi+1),i=0,1,2,⋯,n−2
已知
n
+
1
n+1
n+1 个节点,
n
n
n 个区间,因此有
n
−
1
n-1
n−1 个衔接点,共生成
n
−
1
n-1
n−1 个方程,即
{
S
0
(
x
1
)
=
S
1
(
x
1
)
S
1
(
x
2
)
=
S
2
(
x
2
)
⋮
S
n
−
2
(
x
n
−
1
)
=
S
n
−
1
(
x
n
−
1
)
\begin{cases} S_0(x_1)=S_1(x_1)\\[2ex] S_1(x_2)=S_2(x_2)\\[2ex] \quad\quad\quad\vdots\\[2ex] S_{n-2}(x_{n-1})=S_{n-1}(x_{n-1}) \end{cases}
⎩
⎨
⎧S0(x1)=S1(x1)S1(x2)=S2(x2)⋮Sn−2(xn−1)=Sn−1(xn−1)
条件3:在所有节点(除了第一节点和最后一个节点)处可导
S i ′ ( x i + 1 ) = S i + 1 ′ ( x i + 1 ) , i = 0 , 1 , 2 , ⋯ , n − 2 \boxed{S_i^\prime(x_{i+1})=S_{i+1}^\prime(x_{i+1}),\quad i=0,1,2,\cdots,n-2} Si′(xi+1)=Si+1′(xi+1),i=0,1,2,⋯,n−2
已知
n
+
1
n+1
n+1 个节点,
n
n
n 个区间,因此有
n
−
1
n-1
n−1 个衔接点,共生成
n
−
1
n-1
n−1 个方程,即
{
S
0
′
(
x
1
)
=
S
1
′
(
x
1
)
S
1
′
(
x
2
)
=
S
2
′
(
x
2
)
⋮
S
n
−
2
′
(
x
n
−
1
)
=
S
n
−
1
′
(
x
n
−
1
)
\begin{cases} S_0^\prime(x_1)=S_1^\prime(x_1)\\[2ex] S_1^\prime(x_2)=S_2^\prime(x_2)\\[2ex] \quad\quad\quad\vdots\\[2ex] S_{n-2}^\prime(x_{n-1})=S_{n-1}^\prime(x_{n-1}) \end{cases}
⎩
⎨
⎧S0′(x1)=S1′(x1)S1′(x2)=S2′(x2)⋮Sn−2′(xn−1)=Sn−1′(xn−1)
条件4:在所有节点(除了第一节点和最后一个节点)处二阶可导
S i ′ ′ ( x i + 1 ) = S i + 1 ′ ′ ( x i + 1 ) , i = 0 , 1 , 2 , ⋯ , n − 2 \boxed{S_i^{\prime\prime}(x_{i+1})=S_{i+1}^{\prime\prime}(x_{i+1}),\quad i=0,1,2,\cdots,n-2} Si′′(xi+1)=Si+1′′(xi+1),i=0,1,2,⋯,n−2
已知
n
+
1
n+1
n+1 个节点,
n
n
n 个区间,因此有
n
−
1
n-1
n−1 个衔接点,共生成
n
−
1
n-1
n−1 个方程,即
{
S
0
′
′
(
x
1
)
=
S
1
′
′
(
x
1
)
S
1
′
′
(
x
2
)
=
S
2
′
′
(
x
2
)
⋮
S
n
−
2
′
′
(
x
n
−
1
)
=
S
n
−
1
′
′
(
x
n
−
1
)
\begin{cases} S_0^{\prime\prime}(x_1)=S_1^{\prime\prime}(x_1)\\[2ex] S_1^{\prime\prime}(x_2)=S_2^{\prime\prime}(x_2)\\[2ex] \quad\quad\quad\vdots\\[2ex] S_{n-2}^{\prime\prime}(x_{n-1})=S_{n-1}^{\prime\prime}(x_{n-1}) \end{cases}
⎩
⎨
⎧S0′′(x1)=S1′′(x1)S1′′(x2)=S2′′(x2)⋮Sn−2′′(xn−1)=Sn−1′′(xn−1)
综上,第一个约束条件得到了 n + 1 n+1 n+1 个方程,第二、三、四个约束条件分别得到了 n − 1 n-1 n−1 个方程,总计 4 n − 2 4n-2 4n−2 个方程,还缺少 2 个方程。
二、求解方程组
函数
S
(
x
)
S(x)
S(x) 的一阶导数和二阶导数为
{
S
i
(
x
)
=
a
i
+
b
i
(
x
−
x
i
)
+
c
i
(
x
−
x
i
)
2
+
d
i
(
x
−
x
i
)
3
S
i
′
(
x
)
=
b
i
+
2
c
i
(
x
−
x
i
)
+
3
d
i
(
x
−
x
i
)
2
S
i
′
′
(
x
)
=
2
c
i
+
6
d
i
(
x
−
x
i
)
\begin{cases} S_i(x)=a_i+b_i(x-x_i)+c_i(x-x_i)^2+d_i(x-x_i)^3\\[2ex] S_i^\prime(x)=b_i+2c_i(x-x_i)+3d_i(x-x_i)^2\\[2ex] S_i^{\prime\prime}(x)=2c_i+6d_i(x-x_i) \end{cases}
⎩
⎨
⎧Si(x)=ai+bi(x−xi)+ci(x−xi)2+di(x−xi)3Si′(x)=bi+2ci(x−xi)+3di(x−xi)2Si′′(x)=2ci+6di(x−xi)
根据条件 1,
S
i
(
x
i
)
=
y
i
S_i(x_i)=y_i
Si(xi)=yi,推导得出:
a
i
=
y
i
\boxed{a_i = y_i}
ai=yi
根据条件 2,
S
i
(
x
i
+
1
)
=
S
i
+
1
(
x
i
+
1
)
S_i(x_{i+1})=S_{i+1}(x_{i+1})
Si(xi+1)=Si+1(xi+1)(即
S
i
(
x
i
+
1
)
=
y
i
+
1
S_i(x_{i+1})=y_{i+1}
Si(xi+1)=yi+1)推导得出:
a
i
+
h
i
b
i
+
h
i
2
c
i
+
h
i
3
d
i
=
y
i
+
1
\boxed{a_i+h_ib_i+h_i^2c_i+h_i^3d_i=y_{i+1}}
ai+hibi+hi2ci+hi3di=yi+1
S i ( x i + 1 ) = a i + b i ( x i + 1 − x i ) + c i ( x i + 1 − x i ) 2 + d i ( x i + 1 − x i ) 3 令 h i = x i + 1 − x i S i ( x i + 1 ) = a i + b i h i + c i h i 2 + d i h i 3 又 S i + 1 ( x i + 1 ) = y i + 1 故, a i + b i h i + c i h i 2 + d i h i 3 = y i + 1 S_i(x_{i+1})=a_i+b_i(x_{i+1}-x_i)+c_i(x_{i+1}-x_i)^2+d_i(x_{i+1}-x_i)^3\\[2ex] 令\quad h_i=x_{i+1}-x_i\\[2ex] S_i(x_{i+1})=a_i+b_ih_i+c_ih_i^2+d_ih_i^3\\[2ex] 又\quad S_{i+1}(x_{i+1})=y_{i+1} \quad \\[2ex] 故, a_i+b_ih_i+c_ih_i^2+d_ih_i^3=y_{i+1} Si(xi+1)=ai+bi(xi+1−xi)+ci(xi+1−xi)2+di(xi+1−xi)3令hi=xi+1−xiSi(xi+1)=ai+bihi+cihi2+dihi3又Si+1(xi+1)=yi+1故,ai+bihi+cihi2+dihi3=yi+1
根据条件 3 ,
S
i
′
(
x
i
+
1
)
=
S
i
+
1
′
(
x
i
+
1
)
S_i^\prime(x_{i+1})=S_{i+1}^\prime(x_{i+1})
Si′(xi+1)=Si+1′(xi+1) 推导得出:
b
i
+
2
h
i
c
i
+
3
h
i
2
d
i
−
b
i
+
1
=
0
\boxed{b_i+2h_ic_i+3h_i^2d_i-b_{i+1}=0}
bi+2hici+3hi2di−bi+1=0
S i ′ ( x i + 1 ) = b i + 2 c i ( x i + 1 − x i ) + 3 d i ( x i + 1 − x i ) 2 = b i + 2 c i h i + 3 d i h i 2 S i + 1 ′ ( x i + 1 ) = b i + 1 + 2 c i + 1 ( x i + 1 − x i + 1 ) + 3 d i + 1 ( x i + 1 − x i + 1 ) 2 = b i + 1 故, b i + 2 c i h i + 3 d i h i 2 − b i + 1 = 0 \begin{aligned} S_i^\prime(x_{i+1})&=b_i+2c_i(x_{i+1}-x_i)+3d_i(x_{i+1}-x_i)^2\\[2ex] &=b_i+2c_ih_i+3d_ih_i^2\\[2ex] S_{i+1}^\prime(x_{i+1})&=b_{i+1}+2c_{i+1}(x_{i+1}-x_{i+1})+3d_{i+1}(x_{i+1}-x_{i+1})^2\\[2ex] &=b_{i+1}\\[2ex] &故,b_i+2c_ih_i+3d_ih_i^2-b_{i+1}=0 \end{aligned} Si′(xi+1)Si+1′(xi+1)=bi+2ci(xi+1−xi)+3di(xi+1−xi)2=bi+2cihi+3dihi2=bi+1+2ci+1(xi+1−xi+1)+3di+1(xi+1−xi+1)2=bi+1故,bi+2cihi+3dihi2−bi+1=0
根据条件 4 ,
S
i
′
′
(
x
i
+
1
)
=
S
i
+
1
′
′
(
x
i
+
1
)
S_i^{\prime\prime}(x_{i+1})=S_{i+1}^{\prime\prime}(x_{i+1})
Si′′(xi+1)=Si+1′′(xi+1) 推导得出:
2
c
i
+
6
h
i
d
i
−
2
c
i
+
1
=
0
\boxed{2c_i+6h_id_i-2c_{i+1}=0}
2ci+6hidi−2ci+1=0
S i ′ ′ ( x i + 1 ) = 2 c i + 6 d i ( x i + 1 − x i ) = 2 c i + 6 d i h i S i + 1 ′ ′ ( x i + 1 ) = 2 c i + 1 + 6 d i + 1 ( x i + 1 − x i + 1 ) = 2 c i + 1 故, 2 c i + 6 d i h i − 2 c i + 1 = 0 \begin{aligned} S_i^{\prime\prime}(x_{i+1})&=2c_i+6d_i(x_{i+1}-x_i)\\[2ex] &=2ci+6d_ih_i\\[3ex] S_{i+1}^{\prime\prime}(x_{i+1})&=2c_{i+1}+6d_{i+1}(x_{i+1}-x_{i+1})\\[2ex] &=2c_{i+1}\\[3ex] 故,&2c_i+6d_ih_i-2c_{i+1}=0 \end{aligned} Si′′(xi+1)Si+1′′(xi+1)故,=2ci+6di(xi+1−xi)=2ci+6dihi=2ci+1+6di+1(xi+1−xi+1)=2ci+12ci+6dihi−2ci+1=0
综上,有
{
a
i
=
y
i
①
a
i
+
h
i
b
i
+
h
i
2
c
i
+
h
i
3
d
i
=
y
i
+
1
②
b
i
+
2
h
i
c
i
+
3
h
i
2
d
i
−
b
i
+
1
=
0
③
2
c
i
+
6
h
i
d
i
−
2
c
i
+
1
=
0
④
\begin{cases} a_i = y_i&①\\[2ex] a_i+h_ib_i+h_i^2c_i+h_i^3d_i=y_{i+1}&②\\[2ex] b_i+2h_ic_i+3h_i^2d_i-b_{i+1}=0&③\\[2ex] 2c_i+6h_id_i-2c_{i+1}=0&④ \end{cases}
⎩
⎨
⎧ai=yiai+hibi+hi2ci+hi3di=yi+1bi+2hici+3hi2di−bi+1=02ci+6hidi−2ci+1=0①②③④
令
m
i
=
S
i
′
′
(
x
i
)
=
2
c
i
m_i=S_i^{\prime\prime}(x_i)=2c_i
mi=Si′′(xi)=2ci,可得
c
i
=
m
i
2
\boxed{c_i =\dfrac{m_i}{2}}
ci=2mi
由 ④ 可得
d
i
=
m
i
+
1
−
m
i
6
h
i
\boxed{d_i=\dfrac{m_{i+1}-m_i}{6h_i}}
di=6himi+1−mi
由 ② 可得
b
i
=
y
i
+
1
−
y
i
h
i
−
h
i
2
m
i
−
h
i
6
(
m
i
+
1
−
m
i
)
\boxed{b_i = \dfrac{y_{i+1}-y_i}{h_i}-\dfrac{h_i}{2}m_i-\dfrac{h_i}{6}(m_{i+1}-m_i)}
bi=hiyi+1−yi−2himi−6hi(mi+1−mi)
由 ③ 可得
h
i
m
i
+
2
(
h
i
+
h
i
+
1
)
m
i
+
1
+
h
i
+
1
m
i
+
2
=
6
[
y
i
+
2
−
y
i
+
1
h
i
+
1
−
y
i
+
1
−
y
i
h
i
]
\boxed{h_im_i+2(h_i+h_{i+1})m_{i+1}+h_{i+1}m_{i+2}=6\Big[\dfrac{y_{i+2}-y_{i+1}}{h_{i+1}}-\dfrac{y_{i+1}-y_i}{h_i}\Big]}
himi+2(hi+hi+1)mi+1+hi+1mi+2=6[hi+1yi+2−yi+1−hiyi+1−yi]
三、端点条件(自由边界)
指定端点二阶导数为 0,即
S
0
′
′
(
x
0
)
=
S
n
−
1
′
′
(
x
n
)
=
0
S_0^{\prime\prime}(x_0)=S_{n-1}^{\prime\prime}(x_n)=0
S0′′(x0)=Sn−1′′(xn)=0
可得:
2
c
0
+
6
d
0
(
x
0
−
x
0
)
=
0
2
c
0
=
0
m
0
=
0
2
c
n
−
1
+
6
d
n
−
1
(
x
n
−
x
n
−
1
)
=
0
2
(
m
n
−
1
2
)
+
6
(
m
n
−
m
n
−
1
6
h
n
−
1
)
h
n
−
1
=
0
m
n
−
1
+
m
n
−
m
n
−
1
=
0
m
n
=
0
2c_0+6d_0(x_0-x_0)=0\\[2ex] 2c_0=0\\[2ex] \boxed{m_0=0}\\[3ex] 2c_{n-1}+6d_{n-1}(x_n-x_{n-1})=0\\[2ex] 2(\dfrac{m_{n-1}}{2})+6(\dfrac{m_n-m_{n-1}}{6h_{n-1}})h_{n-1} =0\\[2ex] m_{n-1}+m_n-m_{n-1}=0\\[2ex] \boxed{m_n=0}\\[2ex]
2c0+6d0(x0−x0)=02c0=0m0=02cn−1+6dn−1(xn−xn−1)=02(2mn−1)+6(6hn−1mn−mn−1)hn−1=0mn−1+mn−mn−1=0mn=0
综上,用矩阵形式表示为:
[
1
0
0
0
⋯
0
h
0
2
(
h
0
+
h
1
)
h
1
0
⋯
0
0
h
1
2
(
h
1
+
h
2
)
h
2
⋯
0
0
0
h
2
2
(
h
2
+
h
3
)
⋯
0
⋮
⋮
⋮
⋮
⋮
0
0
0
0
⋯
1
]
[
m
0
m
1
m
2
m
3
⋮
m
n
]
=
6
[
0
y
2
−
y
1
h
1
−
y
1
−
y
0
h
0
y
3
−
y
2
h
2
−
y
2
−
y
1
h
1
y
4
−
y
3
h
3
−
y
3
−
y
2
h
2
⋮
0
]
\left[ \begin{matrix} 1 & 0 & 0 & 0 & \cdots & 0\\ h_0 & 2(h_0+h_1) & h_1 & 0 & \cdots & 0\\ 0 & h_1 & 2(h_1+h_2) & h_2 & \cdots & 0\\ 0 & 0 & h_2 & 2(h_2+h_3) & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & & \vdots\\ 0 & 0 & 0 & 0 & \cdots & 1\\ \end{matrix} \right] \left[ \begin{matrix} m_0 \\ m_1 \\ m_2 \\ m_3 \\ \vdots \\ m_n \\ \end{matrix} \right]=6 \left[ \begin{matrix} 0 \\ \dfrac{y_{2}-y_{1}}{h_{1}}-\dfrac{y_{1}-y_0}{h_0} \\ \dfrac{y_{3}-y_{2}}{h_{2}}-\dfrac{y_{2}-y_1}{h_1} \\ \dfrac{y_{4}-y_{3}}{h_{3}}-\dfrac{y_{3}-y_2}{h_2} \\ \vdots \\ 0 \\ \end{matrix} \right]
1h000⋮002(h0+h1)h10⋮00h12(h1+h2)h2⋮000h22(h2+h3)⋮0⋯⋯⋯⋯⋯0000⋮1
m0m1m2m3⋮mn
=6
0h1y2−y1−h0y1−y0h2y3−y2−h1y2−y1h3y4−y3−h2y3−y2⋮0
python 代码实现
import numpy as np
import matplotlib.pyplot as plt
def cubic_spline_interpolation(x, y):
n = len(x) # n 个插值节点,将曲线分成 n-1 个区间,每个区间构造一个三次函数(4个参数),则共有 4(n-1)个参数待求解
h = np.zeros(n - 1)
for i in range(0, n - 1):
h[i] = x[i + 1] - x[i]
A = np.zeros((n, n))
B = np.zeros(n)
for i in range(1, n - 1):
A[i, i - 1] = h[i - 1]
A[i, i] = 2 * (h[i - 1] + h[i])
A[i, i + 1] = h[i]
B[i] = 6 * ((y[i + 1] - y[i]) / h[i] - (y[i] - y[i - 1]) / h[i - 1])
A[0, 0] = A[n - 1, n - 1] = 1
B[0] = B[n - 1] = 0
m = np.linalg.inv(A) @ B.T
b = np.zeros(n - 1)
d = np.zeros(n - 1)
a = y
c = m / 2
for i in range(0, n - 1):
d[i] = (m[i + 1] - m[i]) / (6 * h[i])
b[i] = (y[i + 1] - y[i]) / h[i] - h[i] * m[i] / 2 - h[i] * (m[i + 1] - m[i]) / 6
return a, b, c, d
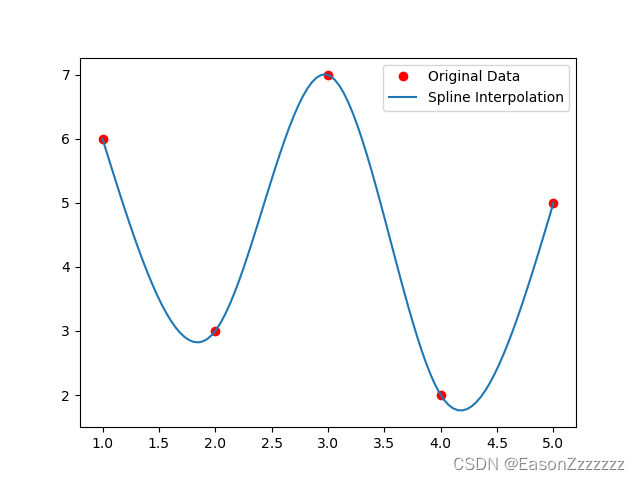
x = np.array([1, 2, 3, 4, 5])
y = np.array([6, 3, 7, 2, 5])
a, b, c, d = cubic_spline_interpolation(x, y)
x_new = np.linspace(1, 5, 100)
num = len(x_new)
y_new = np.zeros(num)
for i, xi in enumerate(x_new):
if x[-1] >= xi >= x[0]:
j = np.searchsorted(x, xi) # 得到 xi 在数组 x 中哪个区间中
if j != 0:
dx = x[j] - x[j - 1]
dy = y[j] - y[j - 1]
y_new[i] = a[j - 1] + b[j - 1] * (xi - x[j - 1]) + c[j - 1] * (xi - x[j - 1]) ** 2 + d[j - 1] * (
xi - x[j - 1]) ** 3
else:
y_new[i] = a[0]
elif xi < x[0]:
y_new[i] = a[0] + b[0] * (xi - x[0]) + c[0] * (xi - x[0]) ** 2 + d[0] * (xi - x[0]) ** 3
elif xi > x[-1]:
y_new[i] = a[-1] + b[-1] * (xi - x[-1]) + c[-1] * (xi - x[-1]) ** 2 + d[-1] * (xi - x[-1]) ** 3
plt.plot(x, y, 'ro', label='Original Data')
plt.plot(x_new, y_new, label='Spline Interpolation')
plt.legend()
plt.show()
结果显示























 269
269











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








