线性代数笔记

第一章

一、行列式的性质

1、性质一：D=

注：是把D的行转为了列。

2、性质二：任意 两行或两列 互换，D=-D1

        推论：若行列式有 两行或两列 相同，则该行列式的值为0。

3、性质三：行列式的某 一行或一列 的公因子可提到外面。

        推论：若行列式 有两行成比例 ，则行列式的值为0。

        推论：若某 一行或一列元素全为0，则该行列式的值为0。

4、性质四：行列式某 一行或一列 的元素可分开。

5、性质五：行列式某一行的k倍加到另一行，该行列式的值不变。

二、行列式的计算

1.化三角法：

注意：交换行或列，记得添负号。

2.降阶法。（适用：将2，3，4行加到第一行，提取公因式（a+b+c+d），让第一行全变为1。）

3.行列式按行（列）展开法：行列式等于它的任一行（列）的各元素与其对应的代数余子式乘积之和，即

①余子式：

② 代数余子式：

③ 推理：行列式任一行（列）的元素与另一行（列）的对应元素的代数余子式乘积之和等于零。

三、线性方程

1.克拉默法则

① 如果线性方程组的系数行列式（D）不等于0，则线性方程有唯一解，解为

例子：

 

 ②如果线性方程组的系数行列式（D）等于0，则线性方程无解或有两个不同解。

 ③若等式右边全为0，则是齐次线性方程。

定理：齐次线性方程有非零解  D=0

          反之，D!=0齐次方程有唯一0解

四、矩阵

1.特殊的矩阵：

①单位矩阵（E）：主对角线上的元素全为1，其余元素为0的矩阵。

②对角矩阵：主对角线以外的元素都是0的矩阵。

性质：（a1，a2......an都不为0，-1可改为其他正整数）

③零矩阵：所有元素都是0的矩阵。    （注意：不同阶数的零矩阵是不相等的。）

④同行矩阵：两个矩阵的行数和列数相等。

2.矩阵的运算

①矩阵的加法and减法：两个同阶矩阵才可进行加减。

②矩阵的数乘：Amn × Bnp = Cmp

3.矩阵的性质（注意）

①在矩阵乘法里面一般AB！=BA。      （即矩阵乘法不满足交换律）

②AB=0不能推出A=0或B=0，AB=AC也不能推出B=C。     （即矩阵乘法不满足消去律）

③

④

⑤ 

⑥   (n为行列式A的行数） （行列式数乘的区别）

⑦ |AB|=|A| × |B|    (矩阵A、B乘积 的 行列式 值等于 行列式A 乘 行列式B）

⑧ A+2=A+2E    （E代表同阶单位矩阵）

五、逆矩阵

1.定义： 矩阵A可逆  |A|！=0

2.求逆矩阵方法（两种 1）： 

3.伴随矩阵：Aij 是|A|中各元素的代数余子式。

 4.|A*|与|A|之间的关系：|A*| = 

5.求二阶逆矩阵：A=，= 1/|A| × 

6.求一阶逆矩阵：A=(2)，=()

六、分块矩阵

1.分块矩阵运算法则：A的行怎么分，B的列就怎么分。

2.分块对角矩阵：若对角的元素都不为0，则有

七、初等变换

1、矩阵等价：矩阵A经过有限次初等变换，变成B；就称A等价于B。记为：AB

2、矩阵的等价标准形：

3、矩阵的三种初等变换：

4、定理：

例如：（1）将A第二行和第三行互换              E（2，3）A 

          （2）将A第二行乘4            E（2（4））A

          （3）将A的第二行的5倍加到第三行               E（3，2（5））A

5、求逆矩阵方法（两种  2）：（A|E）=（E|）

 注意：1.E代表同阶单位矩阵                 2.行和列只能选其一进行变换

八、矩阵的秩

1.秩的定义：矩阵中不为0的子式的最高阶数。

求秩的方法：进行多次初等变换，让矩阵主对角线下全为0。

2.阶梯形矩阵的定义：①矩阵的0行在矩阵最下一行 。

                                   ②非0行的第1个不为零的元素的列标随着行标的递增而严格增大。 

3.增广矩阵和系数矩阵：

 4.满秩矩阵：可逆矩阵（|A|！=0）+矩阵的秩等于阶数

、

九、解线性方程组

1.主元：梯形矩阵非0行首个不为0的元素。                                                                                       

2.写出对应增广矩阵，将主元元素变为1，变换完将矩阵写成线性方程组。

注意：若要设未知解，不找主元所在列。

3.性质一：线性方程组有解 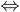 系数矩阵的秩r(A)=增广矩阵的秩r(A,B)

性质二：线性方程有一个解 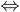 系数矩阵的秩r(A)=增广矩阵的秩r(A,B)=未知数的个数n

性质三：线性方程有无穷解 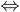 系数矩阵的秩r(A)=增广矩阵的秩r(A,B)<未知数的个数n

4.齐次线性方程组和非齐次线性方程组：

十、线性相关

1.线性相关的定义：

推论：①包含0向量的任何向量组是线性相关的。  

           ②一个0向量，必相关；一个非0向量，必不相关。

           ③不是线性相关，就是线性无关。

2.线性相关的性质：

①a1,a2,......,a5相关至少一个向量可由其余向量表示

②向量个数m > 向量维数（向量一行或一列的个数）n，m个n维向量线性相关

3.极大无关组满足条件：①a1,a3线性无关        ②每个向量均可由 a1,a3表示

注意：向量的秩=极大无关组含向量的个数

注意：0 < 秩的数量 < 向量个数和向量维数两者中的偏小值

4.极大无关组求法：

①求极大无关组的个数

②非0行主元非0的所在列是线性无关组。

③将矩阵变为最简形矩阵（可求用极大无关组表示）

插入知识：最简形举证：指的是矩阵中非零行的第一个非零元素全是1，且非零行的第一个元素1所在的列的其余元素全是0的矩阵。

5.线性相关的判定：

 1）n个n维向量 ：（1，0，3） （2，4，3） （5，2，0）//三个三维向量

         

2）向量构成矩阵的秩 = 向量的个数  （线性无关）

     向量构成矩阵的秩 < 向量的个数  （线性相关）

3.例题：

十一、向量空间

1.含义：设 v为 n 维向量的集合，如果集合 v 非空，且集合v对于加法及数乘两种运算封闭，那么就称集合 v为向量空间。（记为：R的n次方）

插入：运算封闭：

 2.证是否向量空间的基==证向量无关

十一、特征向量

1.特征向量：

2.特征值：（看上面）。

插入：特征值不为0！！！特征向量不为0向量！！！

3.如何求特征值：

4.如何求特征向量：