【信号分解】基于辛几何模态SGMD实现信号数据分解附Matlab代码

 ✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知,完整Matlab代码及仿真咨询内容私信。

🌿 往期回顾可以关注主页，点击搜索

⛄ 内容介绍

据辛几何模态分解SGMD，这是一个非常有趣和有挑战性的领域。辛几何模态分解SGMD是一种新兴的数学方法，它可以用来分解复杂的数据集，并揭示隐藏在数据中的模态结构。辛几何模态分解SGMD的研究已经在多个领域取得了显著的成果，包括图像处理、信号处理和模式识别等。

辛几何模态分解SGMD的核心思想是将数据表示为多个模态的组合，每个模态都对应着数据的一个特征。这种分解方法可以提供更好的数据表达能力，使得我们能够更好地理解和分析数据。辛几何模态分解SGMD的应用非常广泛，它可以用于数据压缩、数据降维、数据恢复和数据分类等任务。

辛几何模态分解SGMD的研究还面临一些挑战。首先，辛几何模态分解SGMD的理论基础还不够完善，需要进一步深入研究。其次，辛几何模态分解SGMD的计算复杂度较高，需要设计高效的算法来解决实际问题。此外，辛几何模态分解SGMD在处理大规模数据集时可能存在一些困难，需要进一步优化算法和提高计算效率。

总的来说，辛几何模态分解SGMD是一个非常有前景和潜力的研究领域。通过深入研究和不断创新，我们可以进一步推动辛几何模态分解SGMD的发展，为各个领域的数据分析和处理提供更加有效和可靠的方法。希望未来能够看到更多关于辛几何模态分解SGMD的研究成果和应用实践。

⛄ 核心代码

​clcclearclose allfs = 5120;time = 1;t = 0:1/fs:time-1/fs;x1_t = 2*(1+0.5*(sin(2*pi*t))).*sin(60*pi*t);x2_t = sin(120*pi*t);x3_t = 0.5*cos(10*pi*t);sig = x1_t + x2_t + x3_t;​% nfft = 2^floor(log2(n)) and use periodogramSGCs = SGMD(sig,fs,1,0.95,0.01);​% nfft = 1024 and use periodogram% SGCs = SGMD(sig,fs,1,0.95,0.01,1024);​% nfft = 256 and use pwelch% SGCs = SGMD(sig,fs,1,0.95,0.01,256,'1');​figure();subplot(4,1,1);plot(sig);xlim([0,length(sig)]);xlim([0,fs*t(end)]);subplot(4,1,2);plot(x1_t);xlim([0,fs*t(end)]);subplot(4,1,3);plot(x2_t);xlim([0,fs*t(end)]);subplot(4,1,4);plot(x3_t);xlim([0,fs*t(end)]);​​figure();[~,b] = size(SGCs);for i = 1:b    subplot(b,1,i);    plot(SGCs(:,i));    xlim([0,fs*t(end)]);end​​

⛄ 运行结果

Fig.1 The same simulation signal as in literature 1.

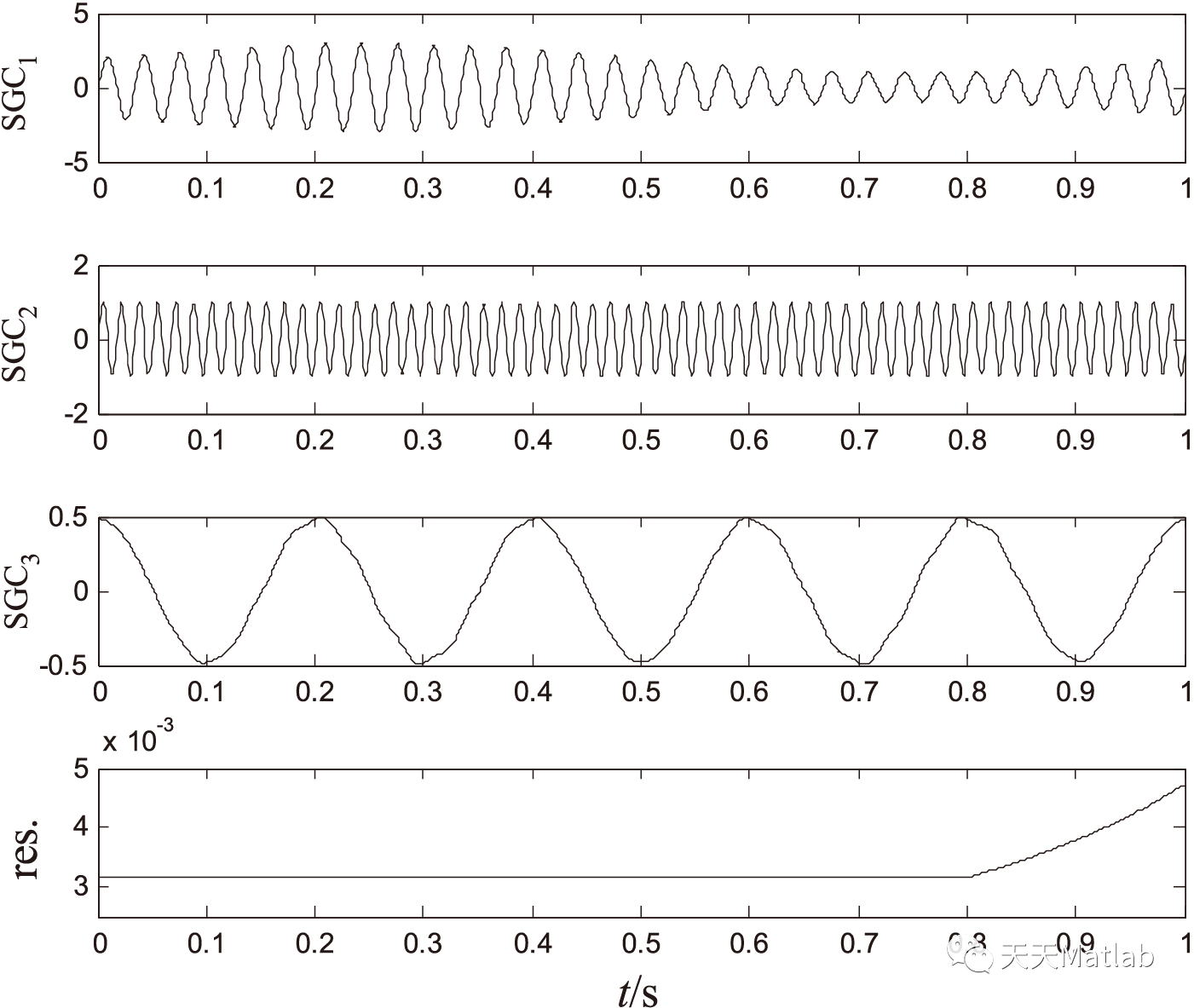
Fig.2 The decomposition results given in the SGMD paper.

Fig.3 Decomposition results of this program (Python)

⛄ 参考文献

[1] Pan H, Yang Y, Li X, et al. Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis[J]. Mechanical Systems and Signal Processing, 2019, 114:189–211. DOI: 10.1016/j.ymssp.2018.05.019.

[2] 潘海洋. 基于辛几何模态分解和支持矩阵机的机械故障诊断方法[D]. 湖南大学, 2019.

⛳️ 代码获取关注我

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料

🍅 仿真咨询

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配

、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合