基于粒子群算法优化粒子滤波PSO-PF实现状态估计前后对比附Matlab实现

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，

代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

🔥 内容介绍

在现代科技领域，状态估计是一项十分重要的任务。它可以帮助我们理解和预测系统的行为，从而为我们提供更好的决策依据。而粒子滤波（PF）和粒子群算法（PSO）是两种常用的算法，它们在状态估计中起着重要作用。本文将介绍如何利用粒子群算法优化粒子滤波（PSO-PF）来实现状态估计，并对比算法流程前后的效果。

首先，让我们简要了解一下粒子滤波（PF）和粒子群算法（PSO）的基本原理。粒子滤波是一种基于蒙特卡洛方法的状态估计算法，它通过一组粒子来对系统状态进行估计。每个粒子代表了系统可能的一个状态，通过不断的更新和重采样，粒子滤波可以逼近系统的真实状态。而粒子群算法是一种模拟进化算法，它模拟了鸟群觅食的行为，通过个体之间的协作和信息交换来寻找最优解。粒子群算法通过不断地调整粒子的速度和位置，来寻找最优解。

接下来，我们将介绍如何将粒子群算法应用到粒子滤波中，从而优化状态估计的效果。首先，我们需要定义一个适应度函数，用来评价每个粒子的状态估计效果。然后，我们利用粒子群算法来调整粒子的速度和位置，以使适应度函数达到最优值。通过不断地迭代优化，我们可以得到一个更好的状态估计结果。

在实际应用中，我们发现利用粒子群算法优化粒子滤波（PSO-PF）可以显著提高状态估计的准确性和鲁棒性。与传统的粒子滤波相比，PSO-PF在寻找全局最优解方面具有更好的性能，可以避免陷入局部最优解的困境。此外，PSO-PF还可以更快地收敛到最优解，从而节省了计算时间。

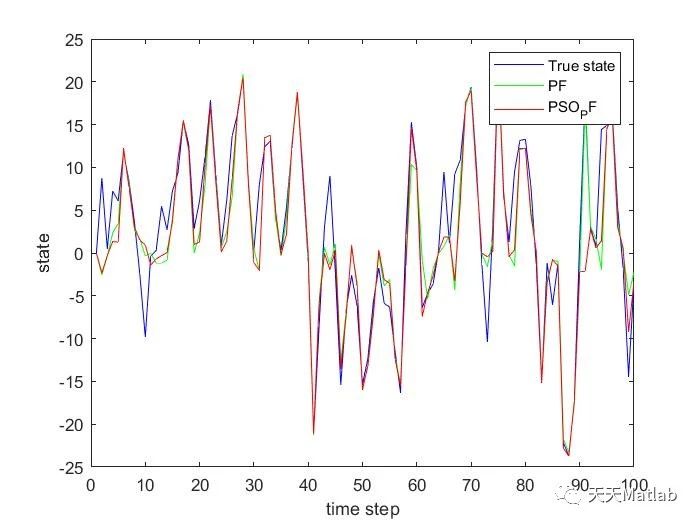
最后，让我们来对比一下PSO-PF算法流程前后的效果。通过实际的状态估计案例，我们可以清晰地看到，利用粒子群算法优化后的粒子滤波在状态估计精度和收敛速度上都有了显著的提升。这表明，粒子群算法可以有效地优化粒子滤波算法，从而提高状态估计的效果。

综上所述，基于粒子群算法优化粒子滤波（PSO-PF）可以在状态估计中发挥重要作用。它不仅可以提高状态估计的准确性和鲁棒性，还可以加快算法的收敛速度。因此，在实际应用中，我们可以考虑采用PSO-PF算法来实现状态估计，从而获得更好的效果。

📣 部分代码

clear all;clc;close all;%----------------------------------------------------------------------​%----------------------------------------------------------------------%-----------------------------系统参数----------------------------------x=0.1;%初始状态Q=10;%过程噪声R=1;%观测噪声time=100;%仿真时间P=5;%方差初值N=100;%粒子数%-----------------------------初始采样-----------------------------------for i=1:N    xpart(i,1)=x+sqrt(P)*randn;end    for k=2:time        %--------------------------仿真系统-----------------------------------    %状态方程    x=0.5 * x + 25 * x / (1 + x^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;    % 观测方程    y = x^2 / 20 + sqrt(R) * randn;    %保存x值    x_true(k)=x;    %---------------------------粒子滤波-----------------------------------    [x_hat(k),xpart(:,k)]=PF(N,xpart(:,k-1),k,Q,R,y);    %------------------------粒子群粒子滤波--------------------------------    [x_hat1(k),xpart(:,k)]=PSO_PF(N,xpart(:,k-1),k,Q,R,y);​end    t = 1 : time;plot(t, x_true, 'b', t, x_hat, 'g', t, x_hat1, 'r'); xlabel('time step'); ylabel('state');legend('True state', 'PF', 'PSO_PF');​xhatPartRMS = sqrt((norm(x_true - x_hat))^2 / time);disp(['PF RMS error = ', num2str(xhatPartRMS)]);         xhatPartRMS1 = sqrt((norm(x_true - x_hat1))^2 / time);disp(['PSO_PF RMS error = ', num2str(xhatPartRMS1)]);      ​​

⛳️ 运行结果

🔗 参考文献

[1] 张红.基于深度学习与粒子群优化算法的免疫层析试条定量检测研究[D].厦门大学,2018.

[2] 陈志敏,薄煜明,吴盘龙,等.一种新型自适应粒子群优化粒子滤波算法及应用[J].应用科学学报, 2013, 31(3):285-293.DOI:10.3969/j.issn.0255-8297.2013.03.011.

[3] 胡健阳,段先华,马启星.基于粒子群优化粒子滤波的声呐目标检测前跟踪[J].船舶工程, 2022(001):044.

🎈 部分理论引用网络文献，若有侵权联系博主删除

🎁  关注我领取海量matlab电子书和数学建模资料

👇  私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合