电学问题解析：静电场、电势与电磁特性,-CSDN博客

本文链接：https://blog.csdn.net/m0_60807167/article/details/134631079

第十一章

解：设四个面的电荷面密度分别为： $\sigma _{1}$ ， $\sigma _{2}$ ， $\sigma _{3}$ ， $\sigma _{4}$ 。

由题可得： $\sigma _{1}s+\sigma _{2}s=0$ ， $\sigma _{3}s+\sigma _{4}s=0$

假设每个面产生的场强全部向右为正。

由静电平衡特性可得： $E_{12}=\frac{\sigma _{1}}{2s}-\frac{\sigma _{2}}{2s}-\frac{\sigma _{3}}{2s}-\frac{\sigma _{4}}{2s} = 0$ , $E_{34}=\frac{\sigma _{1}}{2s}+\frac{\sigma _{2}}{2s}+\frac{\sigma _{3}}{2s}-\frac{\sigma _{4}}{2s} = 0$

解，得 $\sigma _{1}=\sigma _{4}=0$ ， $\sigma _{2}=-\sigma _{3}=0$

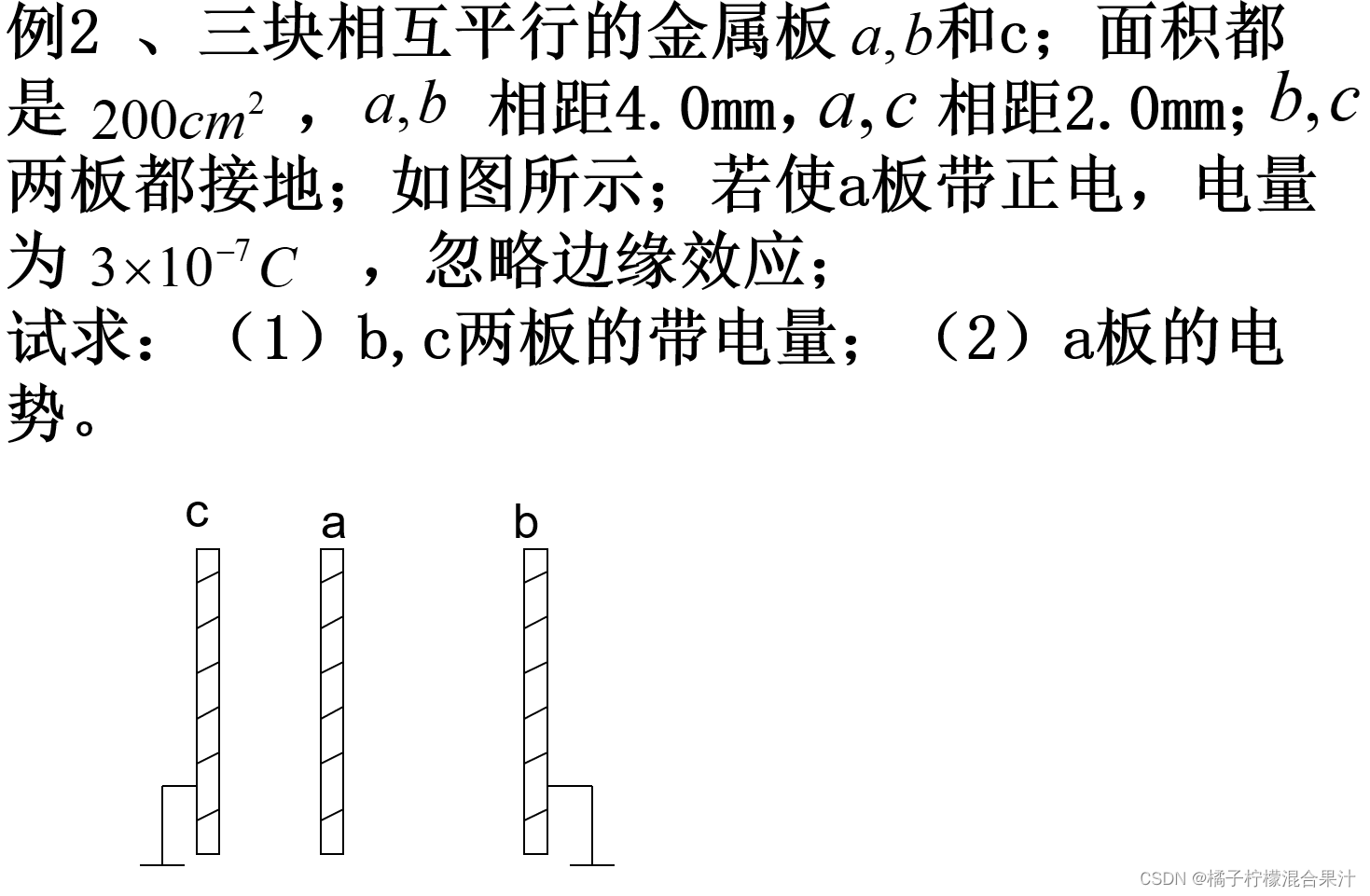
若导体板上分别有电荷q，Q。则有 $\sigma _{1}=\sigma _{4}=\frac{q+Q}{2S}$ , $\sigma _{2}=-\sigma _{3}=\frac{q-Q}{2S}$

解：

（1）由静电平衡可得： $q_{a}=q_{b}+q_{c}$

又 $U_{ac} = U_{ab}$ ，且 $E_{ab} = \frac{q_{ar}}{\varepsilon S}$ ， $E_{ac} = \frac{q_{al}}{\varepsilon S}$ （该式中q表示带+q那面的电荷量）

则可得 $q_{al}=2q_{ar}$ ，且： $q_{al}=-q_{a},q_{ar}=-q_{b}$

最终： $q_{b} = -1*10^{-7}C$ ， $q_{c} = -2*10^{-7}C$

（2） $U_{ab}=\frac{\sigma }{\varepsilon }d_{2}=\frac{q_{c}}{\varepsilon S}d_{2}$

解：这里需要知道一个结论：球面外的电势与将电荷集中在球心的点电荷的电势相同。球面内的电势处处相等，为等势体。

（1）由电势叠加原理可得： $U = k(\frac{q}{R}-\frac{q}{R_{1}}+\frac{q+Q}{R_{2}})$

(2) 内表面电势： $Uin = Uout = k(\frac{q}{R_{1}} -\frac{q}{R_{1}}+ \frac{q+Q}{R_{2}})=k\frac{q+Q}{R_{2}}$

电势差： $U_{1} = kq(\frac{1}{R}+\frac{1}{R_{1}})$

(3) 若外球壳接地，外球壳的电势为0，由静电平衡可知，内部状态不受外部影响而改变，则

$U_{qiu} = kq(\frac{1}{R} - \frac{1}{R_{1}})$

解： $C=\frac{q}{U}$ ， $E=\frac{q}{\varepsilon S}$

可得： $C= \frac{E\varepsilon S}{U}$ 、

则 $\frac{C}{S} = \frac{E\varepsilon }{U}$ ，代入数据即可。

解：正电荷聚集在右半球面，负电荷聚集在左半球面。

解：由 $P =\sigma$ ，左端穿入，则 $\theta =\pi$ ，右边穿出，则 $\theta =0$ ，那么左端带负电，右端带正电。

解：电压断开后，q不变。

设两个容器的电容为C1，并联后的电容为：C=2C1

电量为： $q =CU = 2C_{1}U$

改变电介质后， $C_{change}=(\varepsilon +1)C$

电压为： $U=\frac{q}{C_{change}} = \frac{2U}{\varepsilon+1 }$

电势差容易得。

解：

（1）由 $E = \frac{q}{\varepsilon d}$ ， $C=\frac{q}{U}$ 得： $E=\frac{CU}{\varepsilon S}$ ，其中 $\varepsilon = \varepsilon _{r}\varepsilon _{0}$ ,

得： $E=1.1*10^{-4}(V/m)$

（2）Q = CU = $5*10^{-9}C$

（3） $P = \sigma ^{{}'}$ ， $P=\chi _{e}\varepsilon _{0}E$

得： ${\sigma }'=4.84*10^{-4} C/m^{2}$

解：

（1） $\sigma =\frac{q}{S}$ ， $E=\frac{\sigma }{\varepsilon }=\frac{q}{\varepsilon \varepsilon _{r}S}$ ， $\varepsilon _{r}= \frac{q}{\varepsilon SE}$

（2） $\sigma ^{{}'}=\sigma (1-\frac{1}{\varepsilon _{r}})$ ，且 $q=\sigma S$

$q^{{}'} = q(1-\frac{1}{\varepsilon _{r}})$

解：

第十二章

解：理解径向，即直径得方向。理解电阻公式中各个量的含义 $R=\rho\frac{l}{S}$ 。

其中S来自电流密度 $j$ 定义式，表示与电流方向垂直的面上的截面积， $l$ 来自电势定义式中的积分路径。

（1）如图，径向上的路径为0.5到1，记每一小份为dr；电流密度中的S上一段有说，就是电流流过的那个面，对于径向来说面积为 $2\pi rl$ ， $l$ 为导线长度。

$dR=\rho \frac{dr}{2\pi rl}$

$R = \int_{0.5*10^{-2}}^{1*10^{-2}}\rho \frac{dr}{2\pi rl}=2.2*10^{-8}\Omega$

（2） $I =\frac{U}{R}$

解：理解上面所说，轻松可得： $dR = \rho \frac{dr}{4\pi r^{2}}$

$R = \int_{R1}^{R2}\frac{dr}{4\pi r^{2}}=\frac{\rho }{4\varpi }(\frac{1}{r1}-\frac{1}{r2})$

解：

（1） $\rho =\frac{E}{j}$

（2）大气距离地面的距离对于地球半径来说远远小，近似地球半径R。

$R=\frac{U}{I}=\frac{U}{4\pi R^{2}j}$

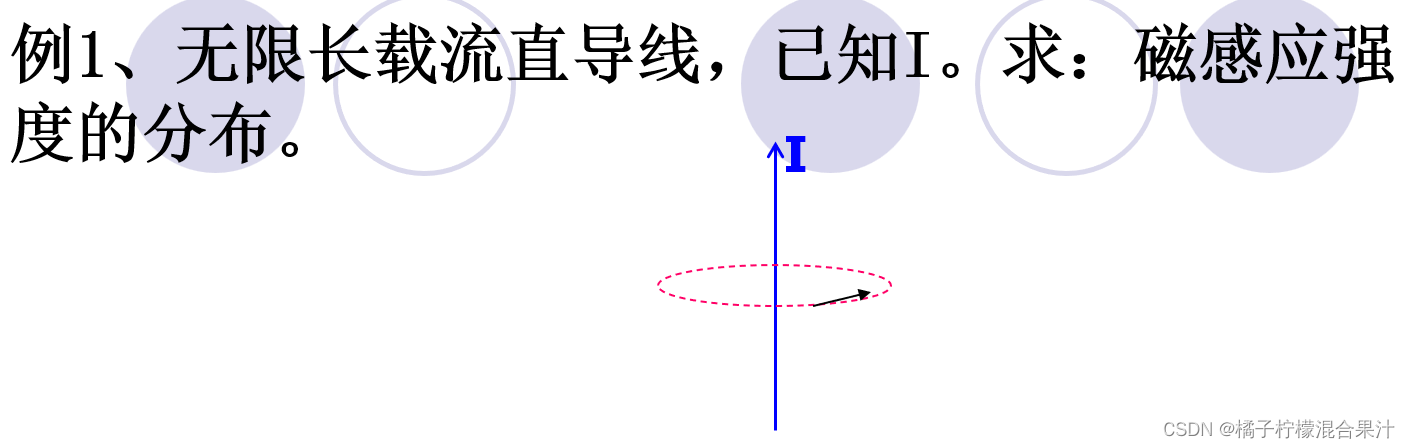
不推导公式，直接记公式即可。

$B = \frac{\mu _{0}}{4\pi }\frac{I}{a}(cosa _{1}-cosa _{2})$

其中 $a$ 为P点到直线的距离。

不推导，公式如下

$B=\frac{\mu _{0}IR^{2}}{2(x^{2}+R^{2})^{3/2}}$

若点到圆面的距离为0，特殊地，有 $B=\frac{\mu _{0}I}{2R}$

解：O点在水平导线连线上，由毕-萨定理得： $Id\vec{l}\times \vec{r}$ 为0，所以水平导线对O的B为0

圆周上，先分析磁感应强度B的方向，由右手关系可知，半圆周上B朝里穿进去，即方向相同。

由上一题的公式可得， $B=\frac{1}{2}\frac{\mu _{0}I}{2R}$

解：

显然直线A，与直线B使用上面例1，弧AB是用上面例2。

$E=\frac{1}{4}\frac{\mu _{0}I}{2R}+\frac{\mu _{0}}{2\pi }\frac{I}{R}$

解：书上有详细解答，直接记公式

$B=\frac{\mu _{0}nI}{2}(cos\beta _{2}-cos\beta _{1})$

解：逆时针转。

电荷随着圆盘的转动而产生电场，就好像半径从0到R有一圈一圈的电流在环绕。所以可以

电荷密度： $\frac{q}{\pi R^{2}}$ 图中黑色单位圆环的面积： $2\pi rdr$ ，其中dr为宽度

单位面积上的单位电荷量： $\frac{q}{\pi R^{2}}\cdot 2\pi rdr$

将 $dI$ 转换为 $dr$ ： $dI=\frac{q}{\pi R^{2}}\cdot \frac{2\pi}{T} rdr = \frac{q}{\pi R^{2}}\cdot wrdr=\frac{qwrdr}{\pi R^{2}}$ （ $T$ 是旋转一圈的时间）

代入 $dB=\frac{\mu _{0}dI}{2r}$ 中，得： $dB = \frac{\mu _{0}qw}{2\pi R^{2}}dr$

所以 $B = \frac{\mu _{0}qw}{2\pi R^{2}}\int_{0}^{R}dr = \frac{\mu _{0}qw}{2\pi R}$

方向为： $\bigodot$

解：

（1） $B_{A} = \frac{\mu _{0}I_{1}}{2\pi \frac{d}{2}} + \frac{\mu _{0}I_{2}}{2\pi \frac{d}{2}} = 4\times 10^{-6} T$ ，方向： $\bigodot$

（2）记 $I_{1}$ 到P为 $x$ ，P到 $I_{2}$ 距离为 $d-x$

$B = \frac{\mu _{0}I}{2\pi x} + \frac{\mu _{0}I}{2\pi (d-x)}= \frac{\mu _{0}I}{2\pi }(\frac{1}{x}+\frac{1}{d-x})$

$\Phi =\oint_{0.1}^{0.3}BdS = \oint_{0.1}^{0.3}\frac{\mu _{0}I}{2\pi }(\frac{1}{x}+\frac{1}{d-x})ldx = 2.2\times 10^{-6}Wb$

解： $\oint_{L}^{}Bdl =2\pi rB= \mu _{0}I$ （B与L的方向重合）

$B=\frac{\mu _{0}I}{2\pi r}$

解：在长直螺线管线圈内的B方向为水平向右。线方向：abcda

$\oint_{L}^{}Bdl = \int_{a}^{b}Bdl+\int_{b}^{c}Bd+\int_{c}^{d}Bd+\int_{d}^{a}Bd$

其中，ab的线方向与B相同，cos = 1；ad、bc同B垂直，cos = 0；dc上没有B。

所以有： $\int_{a}^{b}Bdl = B\overline{ab}=\mu _{0}I\cdot n\overline{ab}$ ( n为单位长度上的匝数）

则有： $B = \mu _{0}nI$

解： $\oint_{L}^{}Bdl = \int_{b}^{a}Bdl +\int_{d}^{c}Bdl = 2B\overline{ab}=\mu _{0}I\cdot n\overline{ab}$

$B=\frac{\mu _{0}nI}{2}$

解：

r > R，有： $\oint_{L}^{}Bdl = 2\pi rB = \mu _{0}I$

$B = \frac{\mu _{0}I}{2\pi r}$

r < R，有： $\oint_{L}^{}Bdl = 2\pi rB = \mu _{0}I\frac{r^{2}}{R^{2}}$

$B=\frac{\mu _{0}I}{2\pi R^{2}}r$

解：设图中长方形的长度为 $l$ ，将长方形分割成宽度为dr的小长方形。

由上题知： $B=\frac{\mu _{0}I}{2\pi R^{2}}r$

那么，小正方形的磁通量为： $d\Phi =BdS = Bldr$

长方形的磁通量为： $\Phi =\int_{0}^{R}\frac{\mu _{0}I}{2\pi R^{2}}rldr = \frac{\mu _{0Il}}{4\pi }$

单位长度磁通量为： $B = \frac{\mu _{0I}}{4\pi }$

第十三章

解：

（1）OA上每点速度不同，每一点的动生电动势：

$d\varepsilon =vBdl = wlBdl$

$\varepsilon =\int_{0}^{l}wB\cdot ldl = \frac{Bwl^{2}}{2}$

方向为：A到O（右手螺旋定则：大拇指指向里，弯曲手指指向v，那么四指根的方向就指向了O，他是F，F给电荷一个洛伦兹力向0移动）

（2）圆盘转动时，将圆盘分成无数根OA并联，那么，电势差和上问相同。

解：

$\varepsilon =\int_{a}^{a+L}(v\times B)dl=\int_{a}^{a+L}v\frac{\mu _{0}I}{2\pi l}dl=\frac{\mu _{0}Iv}{2\pi }ln\frac{a+L}{a}$

方向：C到A

物理电磁学考试例题解析

第十一章

第十二章

第十三章