三、多元线性回归模型（计量经济学学习笔记(2)

E ( u i ) = 0 ( i = 1 , 2 , . . . , n ) E(u_i)=0(i=1,2,…,n) E(ui​)=0(i=1,2,…,n)

用矩阵可表示为

E ( U ) = E [ u 1 u 2 . . . u n ] = [ E ( u 1 ) E ( u 2 ) . . . E ( u n ) ] = [ 0 0 . . . 0 ] \begin{gathered} E(U)=E \begin{bmatrix} u_1 \\ u_2 \\ … \\ u_n \end{bmatrix} = \begin{bmatrix} E(u_1) \\ E(u_2) \\ … \\ E(u_n) \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ … \\ 0 \end{bmatrix} \end{gathered} E(U)=E⎣⎢⎢⎡​u1​u2​…un​​⎦⎥⎥⎤​=⎣⎢⎢⎡​E(u1​)E(u2​)…E(un​)​⎦⎥⎥⎤​=⎣⎢⎢⎡​00…0​⎦⎥⎥⎤​​

• 2. 同方差和无自协相关假定

随机扰动项互不相关且方差相同。

• 3. 随机扰动项与解释变量不相关假定

C o v ( X j i , u i ) = 0 Cov(X_{ji},u_i)=0 Cov(Xji​,ui​)=0        ( j = 2 , 3 , . . . , k ; i = 1 , 2 , . . . , n ) (j=2,3,…,k;i=1,2,…,n) (j=2,3,…,k;i=1,2,…,n)

• 4. 无多重共线性假定
• 5. 正态性假定

随机扰动项 u i u_i ui​服从正态分布

u i u_i ui​~ N ( 0 , σ 2 ) N(0,σ^2) N(0,σ2)

---

②多元线性回归模型的估计

==================================================================================

2.1 多元线性回归模型参数的最小二乘估计

---

按最小二乘原则，采用使估计的剩余平方和最小的原则去确定样本回归函数:

∑ e i = Y i − ( β 1 ^ + β 2 ^ X 2 i + β 3 ^ X 3 i + . . . + β k ^ X k i ) \sum{e_i}=Y_i-(\hat{β_1}+\hat{β_2}X_{2i}+\hat{β_3}X_{3i}+…+\hat{β_k}X_{ki}) ∑ei​=Yi​−(β1​^​+β2​​X2i​+β3​^{​X3i​+…+βk​}​Xki​)

使残差平方和 ∑ e i 2 \sum{e_i^2} ∑ei2​最小，其必要条件是

偏导 ∂ ( ∑ e i 2 ) ∂ β j ^ = 0 ( j = 1 , 2 , . . . , k ) \frac{\partial(\sum{e_i^2})}{\partial \hat{\beta _j}}=0 (j=1,2,…,k) ∂βj​^​∂(∑ei2​)​=0(j=1,2,…,k)

即

[ ∑ e i ∑ X 2 i e i . . . ∑ X k i e i ] = [ 1 1 . . . 1 X 21 X 22 . . . X 2 n . . . . . . . . . X k 1 X k 2 . . . X k n ] [ e i e i . . . e n ] = X ′ e = [ 0 0 . . . 0 ] \begin{gathered} \begin{bmatrix} \sum{e_i} \\ \sum{X_{2i}e_i} \\ … \\ \sum{X_{ki}e_i} \end{bmatrix} =\begin{bmatrix} 1&1&…&1 \\ X_{21}&X_{22}&…&X_{2n} \\ …&…&&… \\ X_{k1}&X_{k2}&…&X_{kn} \end{bmatrix} \begin{bmatrix}e_i \\ e_i \\ … \\ e_n \end{bmatrix} =X’e=\begin{bmatrix}0\\0\\…\\0 \end{bmatrix} \end{gathered} ⎣⎢⎢⎡​∑ei​∑X2i​ei​…∑Xki​ei​​⎦⎥⎥⎤​=⎣⎢⎢⎡​1X21​…Xk1​​1X22​…Xk2​​…​1X2n​…Xkn​​⎦⎥⎥⎤​⎣⎢⎢⎡​ei​ei​…en​​⎦⎥⎥⎤​=X′e=⎣⎢⎢⎡​00…0​⎦⎥⎥⎤​​

其中 X ′ X’ X′为样本观测矩阵X的转置矩阵。

对样本回归函数式 Y = X β ^ + e Y=X\hat{β}+e Y=Xβ^​+e两边同乘样本观测矩阵X的转置矩阵 X ′ X’ X′，有

X ′ Y = X ′ X β ^ + X ′ e X’Y=X’X\hat{\beta}+X’e X′Y=X′Xβ^​+X′e

由极值条件式，故有：

X ′ Y = X ′ X β ^ X’Y=X’X\hat{\beta} X′Y=X′Xβ^​

由古典假定条件中的无多重共线性假定，可知 ( X ′ X ) − 1 (X’X)^{-1} (X′X)−1存在，用 ( X ′ X ) − 1 (X’X)^{-1} (X′X)−1左乘上述方程两端，可得多元线性回归模型参数向量β最小二乘估计式的矩阵表达式为：

β ^ = ( X ′ X ) − 1 X ′ Y \hat{\beta}=(X’X)^{-1}X’Y β^​=(X′X)−1X′Y

由该式可以看出，参数估计量是样本观测值的函数。

---

2.2参数最小二乘估计的性质

---

①线性

最小二乘估计的参数估计量是被解释变量观测值 Y i Y_i Yi​的线性组合。即 β j ^ ( j = 1 , 2 , . . . , k ) \hat{\beta_{j}}(j=1,2,…,k) βj​^​(j=1,2,…,k)为 Y i Y_i Yi​的线性函数。

②无偏性

β ^ \hat{\beta} β^​是 β \beta β的无偏估计。

③最小方差性

参数向量 β \beta β的最小二乘估计量 β ^ \hat{\beta} β^​是 β \beta β的所有线性无偏估计量中方差最小的估计量。

---

2.3OLS估计的分布性质

---

在古典假定下， β j ^ ( j = 1 , 2 , . . . , k ) \hat{\beta_{j}}(j=1,2,…,k) βj​^​(j=1,2,…,k)服从正态分布，即：

β j ^ \hat{\beta_{j}} βj​^​~ N [ β j , σ 2 c j j ] N[\beta_j,\sigma^2c_{jj}] N[βj​,σ2cjj​]

c j j c_jj cj​j是矩阵 ( X ′ X ) − 1 (X’X)^{-1} (X′X)−1中第j行第j列位置的元素。

---

2.4 随机扰动项的方差估计

---

σ ^ 2 = ∑ e i 2 n − k \hat{\sigma}^2=\frac{\sum e_i^2}{n-k} σ^2=n−k∑ei2​​是随机扰动项方差 σ 2 \sigma^2 σ2的无偏估计。

则 V a r ( β ^ 2 ) = σ ^ 2 c j j = ( ∑ e i 2 n − k ) c j j Var(\hat{\beta}_2)=\hat{\sigma}^2c_{jj}=(\frac{\sum e_i^2}{n-k})c_{jj} Var(β^​2​)=σ2cjj​=(n−k∑ei2​​)cjj​

③多元线性回归模型的假设检验和区间估计

=========================================================================================

---

3.1 拟合优度检验

---

多重可决系数

多重可决系数可表示为

R 2 = E S S T S S = 1 − R S S T S S = 1 − ∑ e i 2 ∑ ( Y i − Y ‾ ) 2 R^{2=\frac{ESS}{TSS}=1-\frac{RSS}{TSS}=1-\frac{\sum{e_i}2}}{\sum{(Y_i-\overline{Y})^2}} R2=TSSESS​=1−TSSRSS​=1−∑(Yi​−Y)2∑ei2​​

多重可决系数是介于0和1之间的一个数。 R 2 R^2 R2越接近1，模型对数据的拟合程度就越好。

也可以用矩阵表示

T S S = ∑ ( Y i − Y ‾ ) 2 = ∑ Y i 2 − n Y ‾ 2 = Y ′ Y − n Y ‾ 2 TSS=\sum{(Y_i-\overline{Y})^2}=\sum {Y_i^{2}-n\overline{Y}}2=Y’Y-n\overline{Y}^2 TSS=∑(Yi​−Y)2=∑Yi2​−nY2=Y′Y−nY2

E S S = β ′ X ′ Y − n Y ‾ 2 ^ ESS=\hat{\beta’X’Y-n\overline{Y}^2} ESS=β′X′Y−nY2^​

R 2 = E S S T S S = β ′ X ′ Y − n Y ‾ 2 ^ ∑ ( Y i − Y ‾ ) 2 = ∑ Y i 2 − n Y ‾ 2 = Y ′ Y − n Y ‾ 2 R^{2=\frac{ESS}{TSS}=\frac{\hat{\beta’X’Y-n\overline{Y}}2}}{\sum{(Y_i-\overline{Y})^2}=\sum {Y_i^{2}-n\overline{Y}}2=Y’Y-n\overline{Y}^2} R2=TSSESS​=∑(Yi​−Y)2=∑Yi2​−nY2=Y′Y−nY2β′X′Y−nY2^​​

修正可决系数

样本容量不变时，随着模型中解释变量的增加，总离差平方和TSS不会改变，而解释平方和ESS可能增大，多重可决系数 R 2 R^2 R2会变大。当被解释变量相同而解释变量个数不同时，这给运用多重可决系数去比较两个模型的拟合程度带来缺陷。

此时用自由度去纠正变差，可以纠正该困难。

修正可决系数 R ‾ 2 = 1 − ∑ e i 2 / ( n − k ) ∑ ( Y i − Y ‾ ) 2 / ( n − 1 ) = 1 − n − 1 n − k ∑ e i 2 ∑ ( Y i − Y ‾ ) 2 \overline{R}^{2=1-\frac{\sum{e_i}2}/(n-k)}{\sum{(Y_i-\overline{Y})^{2}/(n-1)}=1-\frac{n-1}{n-k}\frac{\sum{e_i}2}}{\sum{(Y_i-\overline{Y})^2}} R2=1−∑(Yi​−Y)2/(n−1)∑ei2​/(n−k)​=1−n−kn−1​∑(Yi​−Y)2∑ei2​​

修正可决系数与未修正可决系数的关系：

R 2 ‾ = 1 − ( 1 − R 2 ) n − 1 n − k \overline{R^2}=1-(1-R2)\frac{n-1}{n-k} R2=1−(1−R2)n−kn−1​

可以看出， k > 1 k>1 k>1时， R ‾ 2 ＜ R 2 \overline{R}^2＜R2 R2＜R2，这意味着随解释变量的增加， R ‾ 2 \overline{R}^2 R2将小于 R 2 R^2 R2。

可决系数 R 2 R^2 R2必定非负；修正可决系数 R 2 ‾ \overline{R^2} R2可能为负值时，规定 R 2 ‾ = 0 \overline{R^2}=0 R2=0。

---

3.2回归方程的显著性检验(F-检验)

---

对回归模型整体显著性的检验，检验假设的形式为：

H 0 : β 2 = β 3 = . . . = β k = 0 H_0:\beta_2=\beta_3=…=\beta_k=0 H0​:β2​=β3​=…=βk​=0

H 1 ： β j ( j = 2 , 3 , . . . , k ) 不 全 为 零 H_1：\beta_j(j=2,3,…,k)不全为零 H1​：βj​(j=2,3,…,k)不全为零

在 H 0 H0 H0成立的条件下，统计量F服从自由度为k-1和n-k的F分布

F = E S S / ( k − 1 ) R S S / ( n − k ) F=\frac{ESS/(k-1)}{RSS/(n-k)} F=RSS/(n−k)ESS/(k−1)​~ F ( k − 1 , n − k ) F(k-1,n-k) F(k−1,n−k)

给定显著性水平，在F分布表中查自由度为k-1和n-k的临界值 F α ( k − 1 , n − k ) F_\alpha(k-1,n-k) Fα​(k−1,n−k)。

将样本观测值代入上式中计算F值，并将F值与临界值 F α ( k − 1 , n − k ) F_\alpha(k-1,n-k) Fα​(k−1,n−k)比较。若 F > F α ( k − 1 , n − k ) F>F_\alpha(k-1,n-k) F>Fα​(k−1,n−k)，

则拒绝原假设 H 0 H_0 H0​，说明各个解释变量联合起来对被解释变量影响显著。

反之若 F < F α ( k − 1 , n − k ) F<F_\alpha(k-1,n-k) F<Fα​(k−1,n−k)，则不能拒绝原假设，说明影响不显著。

F统计量与可决系数有如下关系：

F = n − k k − 1 R 2 1 − R 2 F=\frac{n-k}{k-1} \frac{R^2}{1-R2} F=k−1n−k​1−R2R2​

即伴随可决系数 R 2 R^2 R2和修正kejuexish R 2 ‾ \overline{R^2} R2的增加，F统计量的值将不断增加。

当 R 2 = 0 R^2=0 R2=0时，F=0。 R 2 R^2 R2越大时，F值也越大； R 2 = 1 R^2=1 R2=1时， F → ∞ F→∞ F→∞。

即对 H 0 : β 2 = β 3 = . . . = β k = 0 H_0:\beta_2=\beta_3=…=\beta_k=0 H0​:β2​=β3​=…=βk​=0的检验，等价于对 R 2 = 0 R^2=0 R2=0的检验。即对 R 2 R^2 R2的显著性检验。

---

3.3回归参数的显著性检验(t检验)

---

多元线性回归不仅仅要获得较高拟合优度的模型，也不仅是要寻找方程整体的显著性，也要对各个整体回归参数作出有意义的估计。因此还必须分别对每个解释变量进行显著性检验。

回归系数估计量服从如下正态分布：

β j ^ = N [ β j , V a r ( β j ^ ) ] \hat{\beta_j}=N[\beta_j,Var(\hat{\beta_j})] βj​^{​=N[βj​,Var(βj​}​)]

其标准化随机变量服从标准正态分布 Z = β j ^ − β j V a r ( β j ^ ) Z=\frac{\hat{\beta_j}-\beta_j}{\sqrt{Var(\hat{\beta_j})}} Z=Var(βj​^​) ​βj​^​−βj​​~ N ( 0 , 1 ) N(0,1) N(0,1)

由前边可知，

V a r ( β j ^ ) = σ 2 c j j Var(\hat{\beta_j})=\sigma^2c_{jj} Var(βj​^​)=σ2cjj​，因为 σ 2 \sigma^2 σ2未知，故 V a r ( β j ^ ) Var(\hat{\beta_j}) Var(βj​^​)也未知。用 σ ^ 2 \hat{\sigma}^2 σ^2代替 σ 2 \sigma^2 σ2作标准化变换，所构造的统计量服从自由度为n-k的t分布。

即 t = β j ^ − β j σ 2 c j j ^ = β j ^ − β j σ ^ c j j t=\frac{\hat{\beta_j}-\beta_j}{\sqrt{\hat{\sigma^2c_{jj}}}}=\frac{\hat{\beta_j}-\beta_j}{\hat{\sigma}\sqrt{c_{jj}}} t=σ2cjj​^​ ​βj​^{​−βj​​=σ}cjj​ ​βj​^​−βj​​~ t ( n − k ) t(n-k) t(n−k)

用t统计量对各个回归参数作显著性检验，

具体过程如下：

①提出检验假设

H 0 ： β j = 0 H_0：\beta_j=0 H0​：βj​=0 ( j = 1 , 2 , . . . , k ) (j=1,2,…,k) (j=1,2,…,k)

H 1 ： β j ≠ 0 H_1：\beta_j≠0 H1​：βj​​=0 ( j = 1 , 2 , . . . , k ) (j=1,2,…,k) (j=1,2,…,k)

②计算统计量

在 H 0 H_0 H0​成立的条件下， t = β j ^ − 0 σ ‾ c j j = β j ^ σ ^ c j j t=\frac{\hat{\beta_j}-0}{\overline{\sigma}\sqrt{c_{jj}}}=\frac{\hat{\beta_j}}{\hat{\sigma}\sqrt{c_{jj}}} t=σcjj​ ​βj​^{​−0​=σ}cjj​ ​βj​^​​~ t ( n − k ) t(n-k) t(n−k)

根据样本观测值计算t统计量的值：

t ∗ = β j ^ σ ^ c j j t*=\frac{\hat{\beta_j}}{\hat{\sigma}\sqrt{c_{jj}}} t∗=σ^cjj​ ​βj​^​​

③检验

给定显著性水平 α \alpha α，查看自由度为n-k的t分布表。得临界值 t α / 2 ( n − k ) t_{α/2}(n-k) tα/2​(n−k)。

若 ∣ t ∗ ∣ ≥ t α / 2 ( n − k ) |t^*|≥t_{α/2}(n-k) ∣t∗∣≥tα/2​(n−k)，即 t ∗ ≤ − t α / 2 ( n − k ) t^*≤-t_{α/2}(n-k) t∗≤−tα/2​(n−k)或 t ∗ ≥ t α / 2 ( n − k ) t^*≥t_{α/2}(n-k) t∗≥tα/2​(n−k)，就拒绝 H 0 H_0 H0​，不拒绝 H 1 H_1 H1​，说明其他解释变量不变的情况下，解释变量X_j对被解释变量Y的影响是显著的。

若 ∣ t ∗ ∣ ＜ t α / 2 ( n − k ) |t^*|＜t_{α/2}(n-k) ∣t∗∣＜tα/2​(n−k)，即 − t α / 2 ( n − k ) ＜ t ∗ ＜ t α / 2 ( n − k ) -t_{α/2}(n-k)＜t^*＜t_{α/2}(n-k) −tα/2​(n−k)＜t∗＜tα/2​(n−k)，就不能拒绝 H 0 H_0 H0​，说明其他解释变量不变的情况下，解释变量X_j对被解释变量Y的影响不显著的。

---

3.4 多元线性回归模型参数的区间估计

---

自我介绍一下，小编13年上海交大毕业，曾经在小公司待过，也去过华为、OPPO等大厂，18年进入阿里一直到现在。

深知大多数Python工程师，想要提升技能，往往是自己摸索成长或者是报班学习，但对于培训机构动则几千的学费，着实压力不小。自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

因此收集整理了一份《2024年Python开发全套学习资料》，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友，同时减轻大家的负担。

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，基本涵盖了95%以上Python开发知识点，真正体系化！

由于文件比较大，这里只是将部分目录大纲截图出来，每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频，并且后续会持续更新

如果你觉得这些内容对你有帮助，可以添加V获取：vip1024c （备注Python）

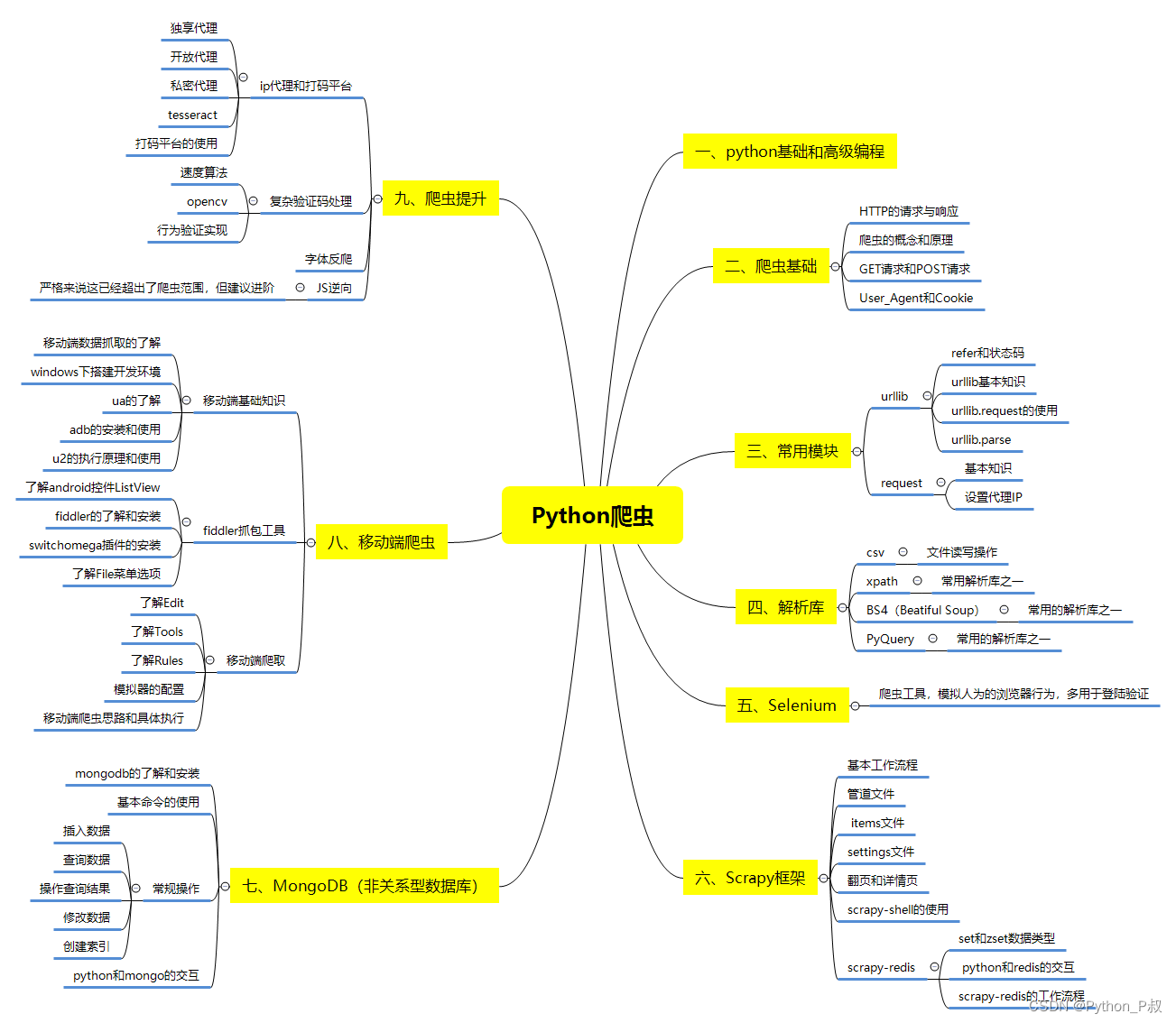
一、Python所有方向的学习路线

Python所有方向的技术点做的整理，形成各个领域的知识点汇总，它的用处就在于，你可以按照下面的知识点去找对应的学习资源，保证自己学得较为全面。

二、Python必备开发工具

工具都帮大家整理好了，安装就可直接上手！

三、最新Python学习笔记

当我学到一定基础，有自己的理解能力的时候，会去阅读一些前辈整理的书籍或者手写的笔记资料，这些笔记详细记载了他们对一些技术点的理解，这些理解是比较独到，可以学到不一样的思路。

四、Python视频合集

观看全面零基础学习视频，看视频学习是最快捷也是最有效果的方式，跟着视频中老师的思路，从基础到深入，还是很容易入门的。

五、实战案例

纸上得来终觉浅，要学会跟着视频一起敲，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。

六、面试宝典

简历模板

到实际当中去，这时候可以搞点实战案例来学习。

六、面试宝典

简历模板