学习笔记-深度学习-神经网络的数学基础

最新推荐文章于 2024-01-08 01:28:37 发布

Pokhanov_

最新推荐文章于 2024-01-08 01:28:37 发布

阅读量362

点赞数

文章标签：深度学习学习笔记

本文链接：https://blog.csdn.net/m0_62382361/article/details/132052189

版权

内容是对《Python深度学习》的摘录、理解、代码实践和遇到的问题。

张量tensor

张量是一个数据容器，矩阵就是一种二阶张量，而张量是矩阵向任意维度的推广，张量的维度通常叫作轴axis，张量轴的个数也叫作阶rank

单独的一个数字就是一个标量张量，标量张量有0个轴

数字组成的数组叫作向量，向量是一阶或一维张量

区分：五维向量与五维张量

五维向量：包含5个元素的向量，只有一个轴，沿着这个轴有五个维度

五维张量：有5个轴，沿着这5个轴可能有任意维度

向量组成的数组叫作矩阵，矩阵是二阶或二维张量，有两个轴（通常叫作行和列）

将多个矩阵打包成一个新的数组，可以得到一个三阶或三维张量，可以将其直观地理解为数字组成的立方体。将多个三阶张量打包成一个数组，就可以创建一个四阶张量，以此类推。深度学习处理的一般是0到4阶的张量，但处理视频数据时可能遇到5阶张量。

求x的轴的个数，可以用x.ndim

(几阶就是有几层相互包含的”[ ]”)

张量的关键属性：

轴的个数（阶数）
形状。是一个整数元组，表示张量沿每个轴的维度大小（元素个数）。
数据类型。张量所包含的数据的类型，可以说float16, float32, float64, uint8等，在TensorFlow还可能遇到string类型的张量。

张量切片

选择张量的特定元素叫作张量切片。

a:b 表示[a,b)，a为空默认从头开始，b为空默认到结尾结束，若为负数则表示与结尾的相对位置

选出第10~99张Image的3种方法：

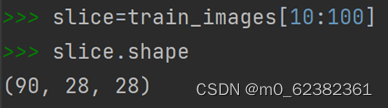
选出所有图像右下角14像素x14像素区域：

选出所有图像中心14像素x14像素区域：

数据批量的概念

深度学习种所有数据张量的第一个轴（0轴）都是样本轴 samples axis，也叫样本维度 samples dimension。

此外，深度学习模型不会一次性处理整个数据集，而是将数据拆分成小批量，对于这种批量张量，第一个轴（0轴）叫作批量轴 batch axis，也叫批量维度 batch dimension。

现实世界的数据张量实例

具体处理数据时遇到的张量几乎总是属于以下类别：

向量数据：形状为（samples, features）的2阶张量，每个样本都是一个数值向量（特征）。

第1个轴为样本轴，第2个轴是特征轴。例如：包括1000个人的年龄、性别和收入的数据集，有1000个样本，每个样本可表示为3个值的向量，可以存储在形状为（1000，3）的2阶张量中

时间序列数据或序列数据：形状为（samples, timesteps, features）的3阶张量，每个样本都是特征向量组成的序列，序列长度为timesteps。

当时间或序列顺序对数据很重要时，应该将数据存储在带有时间轴的3阶张量中。例如：包括30小时内每分钟故事最高、最低价格的数据集（每小时作为一个样本），则有30个样本，每个样本60分钟，包括2个特征，可以存储在形状为（30，60，2）的张量中。

图像数据：形状为（samples, height, width, channels）的4阶张量，每个样本都是一个二维像素网格，每个像素由一个channel向量表示。
视频数据：形状为（samples, frames, height, width, channels）的5阶张量，每个样本都是由图像组成的序列，序列长度为frames。

张量运算tensor operaion

深度神经网络中的所有变换也都可以简化为对数值数据张量的一些张量运算 tensor operation或张量函数 tensor function.

基本张量运算：

点积运算dot
加法运算 +
relu运算。relu(x)就是max(x,0)，relu代表“修正线性单元” rectified linear unit

逐元素 element-wise运算：即该运算分别应用于张量的每个元素，其中relu运算和加法运算都是逐元素运算。

广播broadcast：将两个形状不同的张量做逐元素运算，在没有歧义且可行的情况下，较小的张量会被广播，以匹配较大张量的形状。广播包括以下两步：

向较小张量添加轴[叫作广播轴 broadcast axis]，使其维度与较大张量相同。
将较小张量沿着新轴重复，使其形状与较大张量相同。

点积dot·：最常见的是应用于两个矩阵，得到的结果是向量。与“*”逐元素乘积区分。最常见的应用是两个矩阵的点积，对于矩阵x和y，当且仅当x.shape[1] == y.shape[0]时，才可以计算它们的点积，点积结果是形状为（x.shape[0], y.shape[1]）的矩阵。

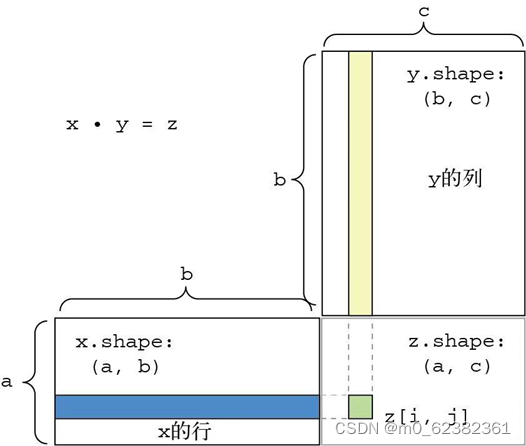
图表 1点积计算的可视化理解

张量变形tensor reshaping：指重新排列张量的行和列，以得到想要的形状。常见的一种特殊的张量变形是转置transpose，矩阵转置是指将矩阵的行和列互换。

张量运算的几何解释

张量的元素可以看作某个几何空间中的点的坐标，因此所有的张量运算都有几何解释。

平移translation可以通过张量加法实现。

旋转rotation，要将一个二维向量[x, y]逆时针旋转theta角，可以通过与一个2x2的矩阵做点积运算实现，这个矩阵为R=[ [cos(theta), -sin(theta)], [sin(theta), cos(theta)] ].

线性变换linear transform：与任意矩阵做点积运算都是线性变换，上面的平移和旋转就是线性变换。

仿射变换affine transform：仿射变换是一次线性变换与一次平移变换的组合（即先与某个矩阵做点积运算再进行向量加法），一个没有激活函数的Dense层就是一个仿射层。关于仿射变换有一个重要结论：不管几个仿射都变换可以简化为一个仿射变换，所以一般一开始就只应用一个仿射变换。

激活函数：一个只由仿射变换组成的神经网络（无论其中有几个仿射变换都可以简化为一个仿射变换）只是一个线性模型，由于激活函数的存在，一连串的Dense层才可以实现复杂的非线性几何变换，从而为深度神经网络提供丰富的假设空间。

深度学习的几何解释

神经网络完全由一系列张量运算组成，而这些张量运算只是输入数据的简单几何变换，因此，神经网络可以解释为高维空间中非常复杂的几何变换，最终达到“为高维空间中复杂、高度折叠的数据流形manifold(指一个连续的表面)找到简洁表示”的目的。

深度学习中训练循环的大致流程

以如下模型为例：每个神经层都对输入数据进行如下变换（层 layer：可以将层看成过滤器，输入一些数据，输出来的数据更有用。将多个层连接起来，从而实现渐进式的数据蒸馏。）

output = relu(dot(input, W) + b)

在这个表达式中，W和b都是张量，均为该层的属性，它们被称为该层的权重weight或可训练参数trainable parameter，分别对应属性kernel和bias（？），这些权重中包含模型从训练数据中学习到的信息。

一开始，这些权重矩阵取较小的随机值，这一步叫作随机初始化random initialization，接下来根据反馈信号逐步调节这些权重，这个逐步调节的过程叫作训练training。

上述过程发生在一个训练循环training loop中，循环会重复直至损失值变得足够小，循环内具体流程如下：

抽取训练样本x和对应目标y_true组成一个数据批量
在x上运行模型（这一步叫作向前传播forward pass）,得到预测值y_pred.
计算模型在这批数据上的损失值，衡量y_pred与y_true之间的差距。
更新模型的所有权重，以略微减小模型在这批数据上的损失值。

其中第一步只是输入/输出的代码，第二三步只是一些张量运算，都不太难。难点在于第四步：更新模型的权重。现在一般用梯度下降gradient descent算法实现优化以此更新模型的权重。

梯度下降算法的要点：模型用到的所有函数，都以一种平滑、连续的方式对输入进行变换，所以这些函数是可微的，也即通过对权重映射到损失值的函数求导（张量运算、张量函数的导数叫作梯度）及链式法则，我们可以直接从系数的变化推测出损失值的变化，而不用进行多次向前传播来寻找系数的优化方向，也能实现在一次更新中同时优化所有系数，而不必使用控制变量法一次只优化一个系数。但要注意某一点的梯度反应的只是该点附近的曲率，所以每次优化的更改不能太大。

利用梯度下降算法的训练方法叫作小批量随机梯度下降mini-batch stochastic gradient descent，简称小批量SGD（随机stochastic是指每批数据都是随机抽取的），具体循环内流程改进如下：

抽取训练样本x和对应目标y_true组成一个数据批量
在x上运行模型（这一步叫作向前传播forward pass）,得到预测值y_pred.
计算模型在这批数据上的损失值，衡量y_pred与y_true之间的差距。
计算损失loss相对于模型参数的梯度（这一步叫作反向传播backward pass）
将参数沿着梯度的反方向移动一小步，比如W-=learning_rate*gradient，从而使这批数据上的损失值减小一些。学习率learning_rate是一个调节梯度下降速度的标量因子。学习率的取值很重要，如果太小会导致需要多次迭代，如果过大可能导致错过达到最小loss的参数。

区别于小批量SGD，还有每次迭代只抽取一个样本和目标的真SGD true SGD，和每次迭代都在所有数据上运行的批量梯度下降batch gradient descent.此外SGD还有多种变体，比如带动量的SGD、Adagrad、RMSprop等，这些变体被称为优化方法optimization method或优化器optimizer。

动量的概念尤其值得关注，它被应用于许多变体。动量解决了SGD的两个问题：收敛速度(?)和局部最小值。使用SGD可能会导致参数陷入局部极小点，而无法找到全局最小值点。使用动量方法可以避免这样的问题，这一方法的灵感来源于物理学：可以将优化过程想象成小球从损失函数曲线上滚下来，如果小球的动量足够大，那么它不会卡在峡谷里，最终会到达全局最低点。动量方法的实现过程是每一步移动小球，不仅要考虑当前的斜率值（当前的加速度），还要考虑当前的速度（由之前的加速度产生）。这在实践中的含义是，更新参数w不仅要考虑当前梯度值，还要考虑上一次参数更新。

反向传播算法backpropagation algorithm

用计算图compu-tation graph进行自动微分.

计算图是一种由运算构成的有向无环图。有了计算图，我们可以将计算看作数据，可以将计算的表达式编码为机器可读的数据然后用于一个程序的输入输出，从而可以实现接收一个计算图作为输入、返回它所对应表达式的导数的程序。

图表 2示例双层模型的计算图表示

反向图就是从loss_val开始，计算每条反向边的导数

根据链式法则，想求反向图中一个节点相对于另一个节点的导数，可以把连接两个节点的路径上每条反向边的导数相乘（如果两个节点a,b间有多条路径，那么grad(a,b)就是所有路径相加）。

以上介绍只是为了理解反向传播的实现，实际上现在已经不需要自己实现反向传播了。

用TensorFlow从头重新实现深度学习

本部分通过不调用Keras API，而是从头手动实践一遍，以此加深对Keras代码的理解。

import numpy as np

import tensorflow as tf

import math

from tensorflow.keras.datasets import mnist





class NaiveDense:

    #   Dense层：密集链接（也叫全连接）的神经层。

    def __init__(self, input_size, output_size, activation):

        self.activation = activation

        #   创建形状为（input_size, output_size)的矩阵w,并将其随机初始化

        w_shape = (input_size, output_size)

        w_initial_value = tf.random.uniform(w_shape, minval=0, maxval=1e-1)

        self.w = tf.Variable(w_initial_value)  # ?Variable()?



        #   创建形状为（output_size,）的零向量b.   ?不用随机初始化吗?

        b_shape = (output_size,)

        b_initial_value = tf.zeros(b_shape)

        self.b = tf.Variable(b_initial_value)



    def __call__(self, inputs):

        #   向前传播

        return self.activation(tf.matmul(inputs, self.w) + self.b)

        # activation是一个逐元素的函数，通常是relu，但最后一层是softmax

        # n路softmax分类层：返回一个由n个概率值（总和为1）组成的数组。

        # tf.matmul()就是两个矩阵的点积



    def weights(self):

        #   获取该层权重的便捷方法

        return [self.w, self.b]





class NaiveSequential:

    #   使用该类将层连接起来，它封装了一个层列表，并定义了一个__call__()方法供外部调用

    def __init__(self, layers):

        self.layers = layers



    def __call__(self, inputs):

        #   ??

        x = inputs

        for layer in self.layers:

            x = layer(x)

        return x



    def weights(self):

        #   ??

        weights = []

        for layer in self.layers:

            weights += layer.weights

        return weights





#   利用上面两个类创建模型

model = NaiveSequential([

    NaiveDense(input_size=28 * 28, output_size=512, activation=tf.nn.relu),

    NaiveDense(input_size=512, output_size=10, activation=tf.nn.softmax)

])

#assert len(model.weights) == 4  # assert断言，在后面的条件不满足时直接返回错误??





#   对MNIST数据进行小批量迭代（把数据分成很多小batch）

class BatchGenerator:

    def __init__(self, images, labels, batch_size=128):

        #assert len(images) == len(labels)  # 图像数据数量和标签数量不匹配直接返回错误

        self.index = 0

        self.images = images

        self.labels = labels

        self.batch_size = batch_size

        self.num_batches = math.ceil(len(images) / batch_size)  # num_batches记录一共分了几个batch,math.ceil()是向上取整



    def next(self):

        #   返回下一个batch的数据及标签

        images = self.images[self.index: self.index + self.batch_size]

        labels = self.labels[self.index: self.index + self.batch_size]

        self.index += self.batch_size

        return images, labels





'''   训练步骤

      1.计算模型由图像数据得出的预测值

      2.根据label计算loss

      3.计算loss相对于模型权重（w,b）的梯度

      4.将权重沿梯度的反方向移动一小步

'''





def one_training_step(model, images_batch, labels_batch):

    # 向前传播，即计算预测值 ?GradientTape? ?tf的调用?

    with tf.GradientTape() as tape:

        predictions = model(images_batch)

        per_sample_losses = tf.keras.losses.categorical_crossentropy(labels_batch, predictions)

        average_loss = tf.reduce_mean(per_sample_losses)

    # 计算损失相对于权重的梯度 ?输出gradients是一个列表，每个元素对应model.weights列表中的权重?

    gradients = tape.gradient(average_loss, model.weights)

    # 利用梯度更新权重,update_weights()的定义在后面

    update_weights(gradients, model.weights)

    return average_loss





learning_rate = 1e-3





def update_weights(gradients, weights):

    for g, w in zip(gradients, weights):

        w.assign_sub(g * learning_rate)  # assign_sub即TensorFlow变量的-=





#   上一部分实现了对每批数据的训练，接下来实现对所有数据的完整训练循环

def fit(model, images, labels, epochs, batch_size=128):

    for epoch_counter in range(epochs):

        print(f"Epoch {epoch_counter}")

        batch_generator = BatchGenerator(images, labels)

        for batch_counter in range(batch_generator.num_batches):

            images_batch, labels_batch = batch_generator.next()

            loss = one_training_step(model, images_batch, labels_batch)

            if batch_counter % 100 == 0:

                print(f"loss at batch {batch_counter}: {loss:.2f}")  # 每训练100个batch输出一次





#   导入MNIST数据集并处理数据、调用训练循环

(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

train_images = train_images.reshape((60000, 28 * 28))

train_images = train_images.astype("float32") / 255

train_images = test_images.reshape((10000, 28 * 28))

test_images = test_images.astype("float32") / 255

fit(model, train_images, train_labels, epochs=10, batch_size=128)



#   对模型进行评估，方法是对模型的预测取argmax(返回值最大的数据的索引，即返回最有可能的数字）,并将其与预期标签比较

predictions = model(test_images)

predictions = predictions.numpy()  # 对TensorFlow张量调用.numpy()，可将其转换为NumPy张量

predicted_labels = np.argmax(predictions, axis=1)

matches = predicted_labels == test_labels

print(f"accuracy: {matches.mean():.2f}")

实际运行时会出问题，但是逻辑大概明白了。

编译所需的3个参数：

优化器 optimizer：模型自我更新的机制

损失函数 loss function：衡量模型在训练数据上的性能

指标 metric：正确分类的样本所占比例