GAT模型数学原理与代码详解（pytorch）

 这是一份用于图注意力网络GAT模型理解的入门教程，采用论文与代码结合的方式阐述GAT注意力机制的实现过程。本文关于数学原理部分不一定完全严谨，如有错误请在评论区指出。 

该模型来自论文：https://arxiv.org/abs/1710.10903https://arxiv.org/abs/1710.10903本文着重分析pytorch框架的模型实现，代码来自开源网络：GitHub - Diego999/pyGAT: Pytorch implementation of the Graph Attention Network model by Veličković et. al (2017, https://arxiv.org/abs/1710.10903)

---

1 频域网络GCN与空域网络GAT

1.1 频域网络GCN

        在图神经网络（GNN）领域中发展出了许多不同的节点信息聚合方式，其中空域GNN与频域GNN是两个十分最重要的发展方向，在之前的文章中我们已经从0开始大致证明了空域GNN的典型算法之一GCN的实现方式：

GCN的基础入门及数学原理_gcn学习-CSDN博客

        在这里稍作复习，我们知道GCN节点信息的聚合方式是取决于图的拉普拉斯矩阵。为了应对空域中不规则图结构无法使用固定卷积核的问题，GCN采用“傅里叶变换”的思想，将图结构变换到频域，完成卷积后再采用逆变换将其变回空间域中。GCN本质上是在频域上对图信号进行滤波。通过拉普拉斯矩阵的特征分解，我们可以将图卷积视为一种频域滤波器。

1.2 空域网络GAT

        GAT（Graph Attention Network）是基于空域图卷积的思想，它通过学习每对节点间的注意力权重，来决定每个节点与邻居节点交互的强度。GAT的核心是通过自注意力机制来加权节点间的信息传播，而不是依赖固定的邻接矩阵。

其步骤如下：

• 节点特征映射
• 计算每个节点之前的注意力分数（权重）
• 邻居信息加权求和
• 多头注意力

其实现代码实现如下：

class GraphAttentionLayer(nn.Module):

    def __init__(self, in_features, out_features, dropout, alpha, concat=True):
        super(GraphAttentionLayer, self).__init__()
        self.dropout = dropout
        self.in_features = in_features
        self.out_features = out_features
        self.alpha = alpha
        self.concat = concat
        self.W = nn.Parameter(torch.zeros(size=(in_features, out_features)))
        nn.init.xavier_uniform_(self.W.data, gain=1.414)
        self.a = nn.Parameter(torch.zeros(size=(2*out_features, 1)))
        nn.init.xavier_uniform_(self.a.data, gain=1.414)
        self.leakyrelu = nn.LeakyReLU(self.alpha)

    def forward(self, x, adj):
        h = torch.bmm(x, self.W)
        N = x.size()[0]
        a_input = torch.cat([h.repeat(1, N).view(N * N, self.out_features), h.repeat(N, 1)], dim=1).view(N, N, 2 * self.out_features)
        attention = self.leakyrelu(torch.matmul(a_input, self.a).squeeze(2))
        zero_vec = -9e15 * torch.ones_like(attention)
        attention = torch.where(adj > 0, attention, zero_vec)
        attention = F.softmax(attention, dim=1)
        attention = F.dropout(attention, self.dropout, training=self.training)
        h_prime = torch.bmm(attention, h)
        if self.concat:
            return F.elu(h_prime)
        else:
            return h_prime

    def __repr__(self):
        return self.__class__.__name__ + ' (' + str(self.in_features) + ' -> ' + str(self.out_features) + ')'


class GAT(nn.Module):
    def __init__(self, nfeat, nhid, n_final_out, dropout, alpha, nheads):
        """Dense version of GAT."""
        super(GAT, self).__init__()
        self.dropout = dropout

        self.attentions = [GraphAttentionLayer(nfeat, nhid, dropout=dropout, alpha=alpha, concat=True) for _ in range(nheads)]
        for i, attention in enumerate(self.attentions):
            self.add_module('attention_{}'.format(i), attention)

        self.out_att = GraphAttentionLayer(nhid * nheads, n_final_out, dropout=dropout, alpha=alpha, concat=False)

    def forward(self, x, adj):
        x = F.dropout(x, self.dropout, training=self.training)
        x = torch.cat([att(x, adj) for att in self.attentions], dim=1)
        x = F.dropout(x, self.dropout, training=self.training)
        x = F.elu(self.out_att(x, adj))
        return x

2 GAT注意力机制的实现

        如果您了解过Transformer模型，那么其中的自注意力机制一定会让您印象深刻，GAT中的注意力机制与Transformer中的注意力机制有异曲同工之妙。如果您没有了解过Transformer也无妨，本文将以最简单易懂的语言来阐述注意力机制的奇妙实现方式。

       GAT中的注意力机制实则是在图中对每个节点之间连接的边赋予权重。如下图示例，GAT中注意力机制即是通过学习得到节点之间的“注意力评分”，可以看出，联系越密切的点其评分越高。

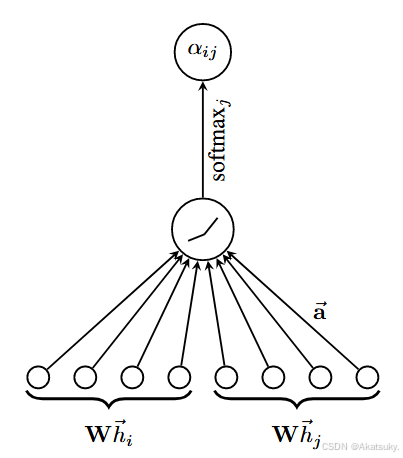
        在论文中注意力评分  的计算公式如下：

        公式描述了注意力评分的计算方法，其中  是一个可学习的矩阵，形状为，其作用是将输入节点的特征映射到高维； 是节点  的输入特征向量，形状为 ； 是一个形状为  的矩阵，其目的是将最终结果映射为一个特定的值，其具体计算流程如下：

        上图中，假设我们初始输入的每个节点都有两个特征， 

        节点  和节点  的输入特征向量经过同一个可学习的参数矩阵 ，其原本的2维特征被映射到5维，之后文中对这两个升维后的特征进行拼接（concatenate），再经过另一个可学习的注意力参数矩阵  映射为一个特征值，这样就得到了节点  对于节点  的注意力分数。（注意，这个注意力是单向的，如果是节点  对于节点  则要重新换顺序计算一次，下文会给出更细致的解释）

---

        上图只是计算了一个方向的注意力分数，实际运用中我们一般是期望得到一个注意力矩阵，矩阵的形状一般为  ，其中为  节点个数，具体实现流程如下图：

        从最简单的例子入手，假如有一个两个节点的图，每个节点有一个输入特征，矩阵W将特征升高到3维度，即 ，我们期望得到的是一个  的注意力矩阵，将该示例带入代码中，得到的流程如下图所示：

        下面以代码角度阐述计算过程：

h = torch.bmm(x, self.W)

        得到结果：

        可以看到经过线性矩阵  的作用后，两个节点的特征从1维扩展到3维。

h.repeat(1, N)

        执行 h.repeat(1, N)，意思是将 h 沿着第二维（特征维度）重复 N 次。因为 N=2，所以会得到以下的张量，形状为 【2,3】（2 是节点数，6 是特征维度）：

h.repeat(N, 1)

        接着，执行 h.repeat(N, 1)，意思是将 h 沿着第一维（节点数维度）重复 N 次。因为 N=2，所以得到以下的张量，形状为 【4,3】（4 是节点数，3 是特征维度）：

torch.cat([h.repeat(1, N), h.repeat(N, 1)], dim=2)

        这个操作沿着第二维（特征维度）拼接两个重复的张量。

•  第一个张量是 h.repeat1(1, N)，它的形状是 【2, 6】。
•  第二个张量是 h.repeat2(N, 1)，它的形状是 【4, 3】。

        执行 torch.cat 后，它们沿着第二维拼接，结果如下：

        这个矩阵  的形状是 【2, 2, 6】，也就是每对节点的特征向量拼接成一个长度为 6 的向量。

torch.cat([h.repeat(1, N), h.repeat(N, 1)], dim=2).view(N, N, 2 * self.out_features)

        最后，通过 .view(N, N, 2 * C) 将张量重新调整为形状 【2, 2, 6】，即每一对节点（共 2x2=4 对）都被拼接了它们的特征，形状为 【N, N, 2 * C】，可表示为：

torch.matmul(a_input, self.a).squeeze(2)

        采用形状为  可学习的注意力参数矩阵 ，使用 torch.matmul 批量矩阵乘法得到最初的注意力矩阵 ：

attention = self.leakyrelu(torch.matmul(a_input, self.a).squeeze(2))
attention = F.softmax(attention, dim=1)

        最终采用 leakyrelu 进行非线性操作，使用softmax归一化后得到最终结果：

        接下来我们就可以采用计算好的注意力系数对节点进行特征更新了： 

        其中  是每个节点更新后的特征向量， 是激活函数。

---

        值得注意的是，对于Transformer的注意力机制来说，作用是求取全局注意力，例如一个包含10个单词的句子，Transfromer期望得到一个  填满的注意力矩阵。然而在GNN领域中我们更注重于节点相邻接的节点对其影响，而不是全局结果。

        对于上文的例子来说，我们实现的功能的计算出每个节点之间的注意力评分，然而这是全局注意力。以下图为例，Node5于Node4并没有直接相连，在这里计算这两点之间的注意力评分是多余的，为了将图结构加入到注意力机制中，作者使用了MASK方法：

zero_vec = -9e15 * torch.ones_like(attention)
attention = torch.where(adj > 0, attention, zero_vec)

        MASK方法的原理也十分简单，就是使用图结构的邻接矩阵于注意力句子的哈达玛乘积(Hadamard product)将不连接节点之间的注意力分数转化为无穷小，即可得到期望的结果。

---

3 多头注意力机制

        关于多头注意力机制的引入，作者在文中这样写到：

 简化来说就是为了增强模型的稳定性与准确性。文中公式如下：

        式中  代表了注意力头的个数，将  个头的注意力机制拼接，最终得到的特征向量的维度也变为原来的  倍，即 

        特别的，如果需要在网络的最后（预测）层上执行多头注意力，那么采用平均值即可得到期望的结果：

        图中每个不同颜色的波浪线即代表不同的注意力头，共同作用更新节点信息。

---