轨迹拟合原理

HMM是什么

隐形马尔科夫模型（HMM）

假设我手里有三个不同的骰子。三个骰子可能投掷出的点数为1-8.

蓝色的骰子代表隐藏状态。所以目前有三种隐藏状态

红色的点数代表观测。有8种点数的可能，8种观测状态。

开始掷骰子，我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。然后我们掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。例如我们可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4

蓝色部分我们称为 状态序列（状态链）

红色部分我们成为 观测序列（观测链）

我们将其抽象为HMM数学模型：

隐马尔可夫模型的 3 个基本问题

1.已知I、O、Q、V，求A和B

2.已知A、B、Q、V、I，求O

3.已知A、B、Q、V、O，求I

我们主要讨论问题3：

也就是，我们已知状态转移矩阵、观测概率矩阵、观测序列，怎么得到最大概率的状态序列？

维特比算法：

这种东西让人望而却步，我来换种方式给大家讲解。说人话：

回到上面的骰子问题，其实我们要解决的问题就是：

没有蓝色部分，只有红色部分；我们需要计算出最大概率的蓝色序列。

我们按照公式算一遍就知道了：

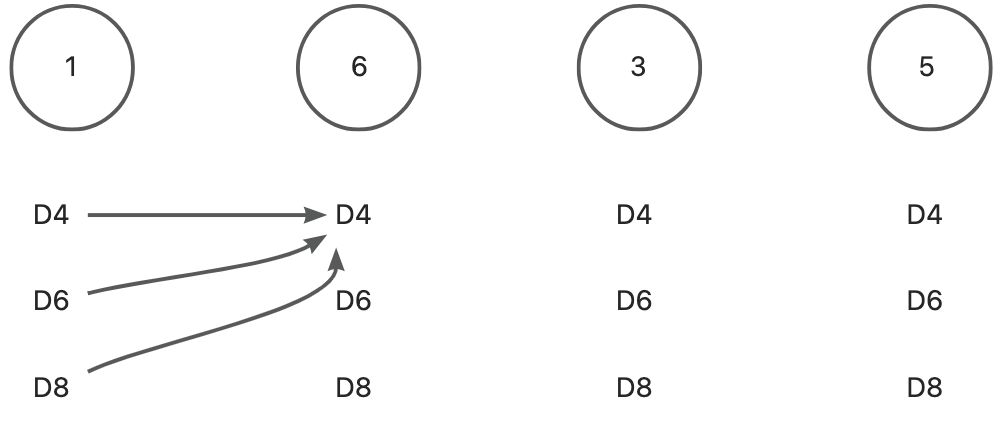
先计算初始状态1:

D4: 1/4 (max)

D6: 1/6

D8: 1/8

初始状态应该是：D4

先计算1->6:

D4->D4: 前序概率(第一个骰子是D4的概率) * 转移概率(D4->D4) * 观测概率(D4出现6的概率) = 1/4*1/3*0 = 0

D6->D4: 前序概率(第一个骰子是D4的概率) * 转移概率(D6->D4) * 观测概率(D4出现6的概率) = 1/4*1/3*1/6 = 1/18

D8->D4: 前序概率(第一个骰子是D4的概率) * 转移概率(D8->D4) * 观测概率(D4出现6的概率) = 1/4*1/3*1/8 = 1/24

6的状态应该是：D6

在计算6->3:

D4->D4: 前序概率(第一个骰子是D4的概率) * 转移概率(D4->D4) * 观测概率(D4出现6的概率) = 1/18*1/3*1/4 = 1/12

D6->D4: 前序概率(第一个骰子是D4的概率) * 转移概率(D6->D4) * 观测概率(D4出现6的概率) = 1/18*1/3*1/6 = 1/18

D8->D4: 前序概率(第一个骰子是D4的概率) * 转移概率(D8->D4) * 观测概率(D4出现6的概率) = 1/18*1/3*1/8 = 1/24

3的状态应该是：D4

依次类推即可推出最大概率的状态序列。

维特比算法在MapMatch中的应用：

mapmatch中如何使用HMM计算路网轨迹呢？

我们把GPS点认为是已知的观测序列O，路网轨迹就是要求的状态序列 I。同时，我们也能计算得出状态转移矩阵和观测矩阵。

说人话：

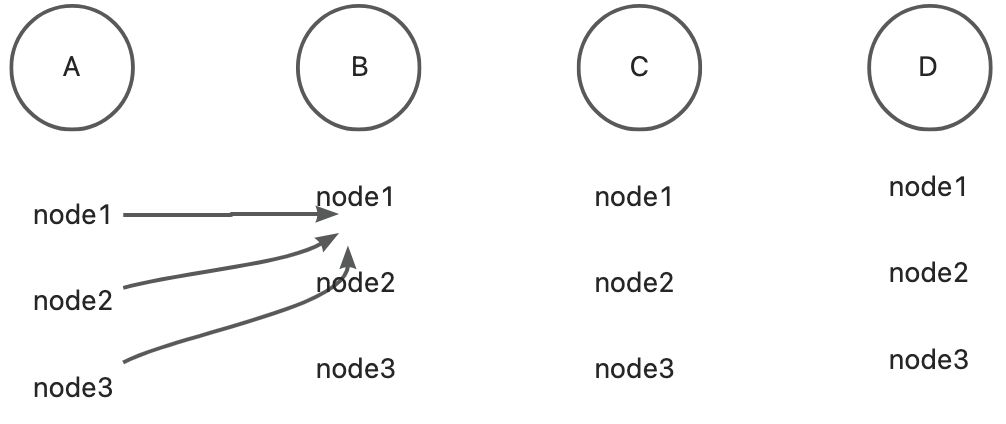
先看点A：

根据node与A的距离计算观测概率，记为b(A1),b(A2),b(A3)；

选出prob_b最大的node作为起始点。

再看点B：

1. 根据node与B的距离计算观测概率，记为prob_b(B1),prob_b(B2),prob_b(B3)；
2. 然后计算A候选点到B候选点的状态转移矩阵:

假设：Anode1->Bnode1，先计算两点直线距离real_d，然后计算两点路径规划距离d，根据两者之差计 算转移概率，prob_d=1/(1+|real_d-d|)

1. 随后选出prob_d+prob_b最大的候选点作为该点的状态点。

依次类推下次，就能得到最大概率的路网点的序列。问题解决。

MapMatch遇到的问题

现在GPS点存在漂移的问题，使得高速点不能被吸附到，产生无法计费的问题。

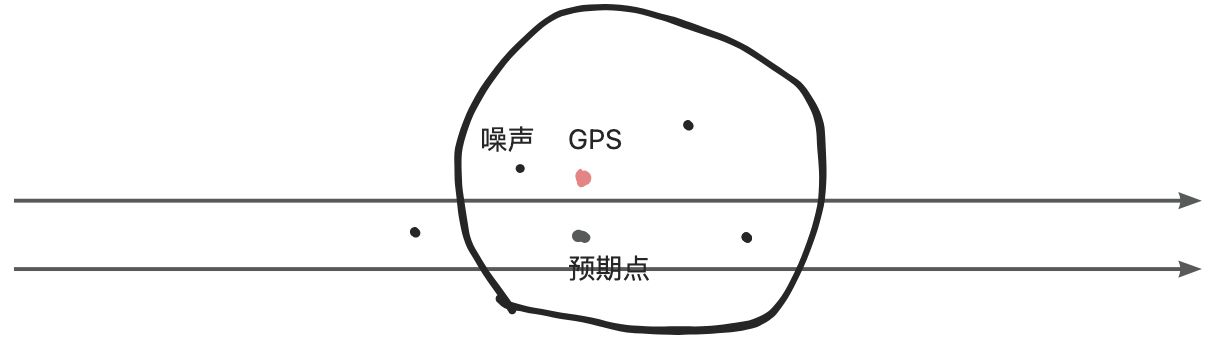
GPS点的飘逸可能造成吸附错误，把状态点吸附到了噪声点上。又或者因为飘逸太远而搜索半径太小，导致预期点就没有进入候选列表。

问题其实分为两个部分：

1. 搜索半径能不能框到高速点（动态设置搜索半径）。
2. 能不能有够大的概率选中高速点（动态提高高速点的概率）。

第一个问题的解法：对与传入引擎的轨迹点，增加每个点的GPS精度；GPS精度与搜索半径成反比，越不精确的点会有更大的搜索半径。这个策略保证高速点一定能被选入候选点。

第二个问题的解法：虽然让预期点进入了候选列表，但是也要有足够大的概率选中高速点。我们可以筛选出所有的高速点，把他的候选概率提高，增加被选中的可能。