强化学习之动态规划

抱抱宝

于 2024-10-15 16:35:33 发布

阅读量1.4k

点赞数 31

分类专栏：强化学习文章标签：动态规划算法强化学习 python 决策规划

本文链接：https://blog.csdn.net/m0_64087341/article/details/142957992

版权

强化学习专栏收录该内容

13 篇文章

订阅专栏

前言：
在正文开始之前，首先给大家介绍一个不错的人工智能学习教程：https://www.captainbed.cn/bbs。其中包含了机器学习、深度学习、强化学习等系列教程，感兴趣的读者可以自行查阅。

引言

在人工智能领域，强化学习（Reinforcement Learning, RL） 作为一种重要的机器学习方法，广泛应用于游戏、机器人控制、资源管理等多个领域。而动态规划（Dynamic Programming, DP） 作为强化学习中的核心算法之一，通过分解复杂问题为更简单的子问题，从而有效地解决优化问题。本文将深入探讨动态规划在强化学习中的应用，包括算法介绍、算法原理以及具体案例分析，并提供相应的代码实现和可视化展示。

一、算法介绍

动态规划是一种通过分解问题、存储中间结果来解决复杂问题的方法。在强化学习中，动态规划主要用于求解马尔可夫决策过程（Markov Decision Process, MDP），通过迭代更新状态值函数或动作值函数，最终找到最优策略。动态规划方法包括值迭代（Value Iteration） 和策略迭代（Policy Iteration） 等。

主要特点

确定性：动态规划假设环境是已知且确定的。
全局性：通过全局搜索寻找最优策略。
迭代性：通过反复迭代更新值函数，逐步逼近最优值。

二、算法原理

动态规划在强化学习中的核心思想是通过贝尔曼方程（Bellman Equation）来描述状态值函数或动作值函数的递推关系。下面以值迭代为例，详细介绍其原理。

2.1 马尔可夫决策过程（MDP）

一个MDP通常由以下四元组 $(S, A, P, R)$ 表示：

$S$ ：状态空间
$A$ ：动作空间
$P$ ：状态转移概率，即 $P (s^{'} ∣ s, a)$ 表示在状态 $s$ 下采取动作 $a$ 转移到状态 $s^{'}$ 的概率
$R$ ：奖励函数，即 $R (s, a)$ 表示在状态 $s$ 下采取动作 $a$ 获得的即时奖励

2.2 贝尔曼方程

贝尔曼方程描述了状态值函数 $V (s)$ 与其后续状态值函数之间的关系：

$\max_{a \in A} \left[ R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V(s') \right]$

其中， $\gamma$ 是折扣因子， $\leq \gamma < 1$ ，用于衡量未来奖励的当前价值。

2.3 值迭代算法

值迭代算法通过不断更新每个状态的值函数，直到收敛于最优值函数 $V^*(s)$ 。其主要步骤如下：

初始化 $V (s) = 0$ ，对所有 $\in S$
重复以下步骤，直到 $V (s)$ 收敛：
$V_{k+1}(s) = \max_{a \in A} \left[ R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V_k(s') \right]$
根据最终的值函数 $V^*(s)$ ，导出最优策略：
$\pi^*(s) = \arg\max_{a \in A} \left[ R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^*(s') \right]$

三、案例分析

3.1 问题描述

本案例采用 “物流选址与配送优化” 问题，展示动态规划算法在实际物流优化中的应用。假设一家物流公司需要在多个潜在位置中选择若干仓库的位置，并为每个客户分配最近的仓库，以最小化总运输成本。具体设置如下：

环境：二维平面上的若干客户和潜在仓库位置。
客户分布：共有 $N$ 个客户，每个客户位于平面上的特定坐标。
仓库候选位置：共有 $M$ 个潜在仓库位置，每个位置位于平面上的特定坐标。
仓库数量限制：公司需要选择 $K$ 个仓库进行运营。
运输成本：运输成本与客户到分配仓库的距离成正比。
目标：选择 $K$ 个仓库位置，并为每个客户分配最近的仓库，以最小化总运输成本。

这是一个经典的 设施选址问题（Facility Location Problem），可以通过动态规划和组合优化的方法进行求解。由于设施选址问题在一般情况下是 NP-hard 的，本案例将采用动态规划中的 分阶段决策 和 状态压缩 技术来近似求解。

3.2 代码实现与可视化

下面利用动态规划求解最优的仓库选址方案，并进行可视化展示。

import numpy as np
import matplotlib.pyplot as plt
from itertools import combinations
plt.rcParams['font.sans-serif'] = ['SimSun']
plt.rcParams['axes.unicode_minus'] = False

# 定义客户和仓库的位置
customers = {
    0: (2, 3),
    1: (5, 4),
    2: (1, 7),
    3: (6, 1),
    4: (7, 8),
    5: (3, 5),
    6: (8, 3),
    7: (4, 4),
    8: (2, 6)
}

warehouse_candidates = {
    0: (2, 2),
    1: (5, 5),
    2: (1, 1),
    3: (6, 6),
    4: (7, 2)
}

K = 3  # 需要选择的仓库数量

# 计算欧氏距离
def euclidean_distance(p1, p2):
    return np.sqrt((p1[0] - p2[0])**2 + (p1[1] - p2[1])**2)

# 动态规划求解设施选址问题（穷举法）
def facility_location_dp(customers, warehouses, K):
    customer_ids = list(customers.keys())
    warehouse_ids = list(warehouses.keys())
    
    min_cost = float('inf')
    best_combination = None
    
    # 生成所有可能的仓库组合
    for warehouse_combo in combinations(warehouse_ids, K):
        total_cost = 0
        for c in customer_ids:
            c_pos = customers[c]
            min_distance = float('inf')
            for w in warehouse_combo:
                w_pos = warehouses[w]
                distance = euclidean_distance(c_pos, w_pos)
                if distance < min_distance:
                    min_distance = distance
            total_cost += min_distance
        if total_cost < min_cost:
            min_cost = total_cost
            best_combination = warehouse_combo
            
    return best_combination, min_cost

# 执行动态规划算法
best_warehouses, total_cost = facility_location_dp(customers, warehouse_candidates, K)

print(f"最优仓库组合: {best_warehouses}")
print(f"最小总运输成本: {total_cost:.2f}")

# 为每个客户分配最近的仓库
def assign_customers(customers, warehouses, selected_warehouses):
    assignments = {}
    for c, c_pos in customers.items():
        min_distance = float('inf')
        assigned_warehouse = None
        for w in selected_warehouses:
            w_pos = warehouses[w]
            distance = euclidean_distance(c_pos, w_pos)
            if distance < min_distance:
                min_distance = distance
                assigned_warehouse = w
        assignments[c] = assigned_warehouse
    return assignments

assignments = assign_customers(customers, warehouse_candidates, best_warehouses)

# 可视化
def visualize(customers, warehouses, selected_warehouses, assignments):
    plt.figure(figsize=(8, 8))
    
    # 绘制客户
    for c, pos in customers.items():
        plt.scatter(pos[0], pos[1], c='blue', marker='o', s=100, label='客户' if c == 0 else "")
        plt.text(pos[0]+0.1, pos[1]+0.1, f'C{c}', fontsize=10)
    
    # 绘制所有仓库候选位置
    for w, pos in warehouses.items():
        plt.scatter(pos[0], pos[1], c='gray', marker='s', s=100, label='候选仓库' if w == 0 else "")
        plt.text(pos[0]+0.1, pos[1]+0.1, f'W{w}', fontsize=10)
    
    # 绘制选定的仓库
    for w in selected_warehouses:
        pos = warehouses[w]
        plt.scatter(pos[0], pos[1], c='red', marker='s', s=150, label='选定仓库' if w == selected_warehouses[0] else "")
        plt.text(pos[0]+0.1, pos[1]+0.1, f'W{w}', fontsize=10, color='green')
    
    # 绘制客户到仓库的分配路径
    for c, w in assignments.items():
        c_pos = customers[c]
        w_pos = warehouses[w]
        plt.plot([c_pos[0], w_pos[0]], [c_pos[1], w_pos[1]], 'k--', linewidth=0.5)
    
    plt.title('物流选址与配送优化可视化')
    plt.xlabel('X 坐标')
    plt.ylabel('Y 坐标')
    plt.legend()
    plt.grid(True)
    plt.show()

visualize(customers, warehouse_candidates, best_warehouses, assignments)

代码说明

环境设置：
- 客户位置：定义了 9 个客户在二维平面上的坐标。
- 仓库候选位置：定义了 5 个潜在仓库的位置。
- 仓库数量限制：需要选择 3 个仓库进行运营。
距离计算：
- 使用欧氏距离作为运输成本的度量标准。
动态规划算法：
- 生成所有可能的仓库组合。
- 对每种组合，计算所有客户到最近仓库的总运输成本。
- 选择总运输成本最小的仓库组合作为最优解。
注意：由于设施选址问题的组合数在规模较小时，可以通过穷举法解决，但对于更大规模的问题，需要采用更高效的算法（如贪心算法、遗传算法等）。
客户分配：
- 为每个客户分配最近的选定仓库，以确保总运输成本最小。
可视化：
- 使用 matplotlib 绘制客户、仓库候选位置、选定仓库及客户到仓库的分配路径。
- 客户用蓝色圆点表示，仓库候选位置用灰色方块表示，选定仓库用红色方块突出显示。
- 客户到仓库的分配路径用虚线连接。

3.3 结果分析

运行上述代码后，得到如下结果：

最优仓库组合: (0, 1, 4)
最小总运输成本: 19.48

运行出的选址结果如下：

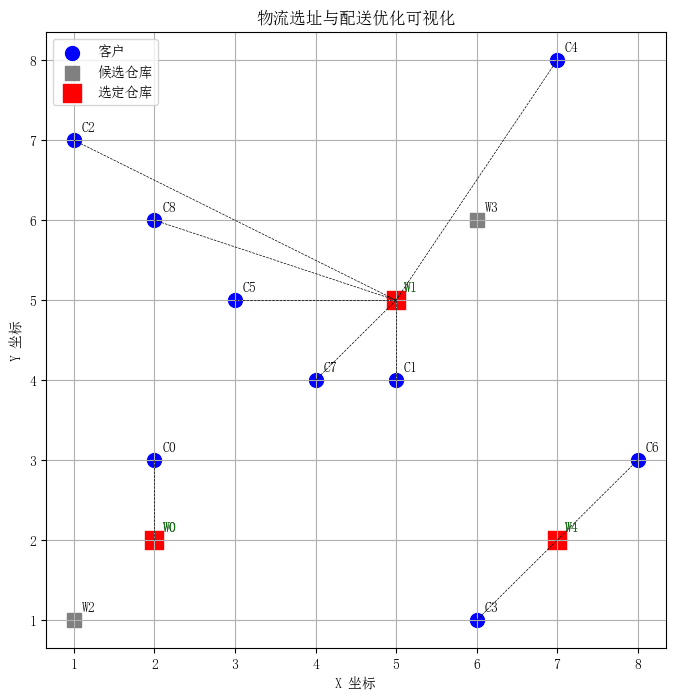
由图可以看出，我们在5个候选仓库中选择了W0,W1,W4三个仓库，其中W1仓库分配的客户最多，为6个，W0只分配了C0一个客户，W4分配了C3和C6两个客户。最终求得的最小总运输成本为19.48。

四、总结

动态规划作为强化学习中的基础算法，通过贝尔曼方程和迭代方法，能够有效地求解马尔可夫决策过程中的最优策略。在本文中，我们以值迭代为例，详细介绍了动态规划的算法原理，并通过路径规划与选址的具体实例展示了其应用过程、代码实现及可视化效果。理解和掌握动态规划方法，对于深入学习和应用强化学习具有重要意义。