数字三角形问题的拓展

一、摘花生

Hello Kitty想摘点花生送给她喜欢的米老鼠。

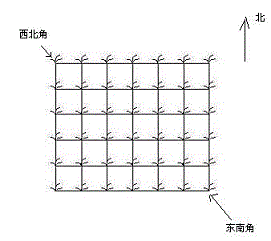
她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。

Hello Kitty只能向东或向南走，不能向西或向北走。

问Hello Kitty最多能够摘到多少颗花生。

输入格式

第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式

对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

数据范围

1≤T≤1001≤T≤100,
1≤R,C≤1001≤R,C≤100,
0≤M≤10000≤M≤1000

输入样例：

2
2 2
1 1
3 4
2 3
2 3 4
1 6 5

输出样例：

8
16

 

 

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int a[N][N];
int f[N][N];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n,m;
        cin>>n>>m;
        for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        cin>>a[i][j];
        for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            f[i][j]=max(f[i-1][j],f[i][j-1])+a[i][j];
        }
        cout<<f[n][m]<<endl;
    }
    return 0;
}

二、最低通行费

【题目描述】

一个商人穿过一个N×N的正方形的网格，去参加一个非常重要的商务活动。他要从网格的左上角进，右下角出。每穿越中间1个小方格，都要花费1个单位时间。商人必须在(2N-1)个单位时间穿越出去。而在经过中间的每个小方格时，都需要缴纳一定的费用。

这个商人期望在规定时间内用最少费用穿越出去。请问至少需要多少费用？

注意：不能对角穿越各个小方格（即，只能向上下左右四个方向移动且不能离开网格）。

【输入】

第一行是一个整数，表示正方形的宽度N (1≤N<100)；

后面N行，每行N个不大于100的整数，为网格上每个小方格的费用。

【输出】

至少需要的费用。

【输入样例】

5
1  4  6  8  10 
2  5  7  15 17 
6  8  9  18 20 
10 11 12 19 21 
20 23 25 29 33

【输出样例】

109

【提示】

样例中，最小值为109=1+2+5+7+9+12+19+21+33。

#include<bits/stdc++.h>
using namespace std;
const int N=110,INF=0x3f3f3f3f;
int a[N][N];
int f[N][N];
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	for(int j=1;j<=n;j++)
	cin>>a[i][j];
	for(int i=1;i<=n;i++)
	for(int j=1;j<=n;j++)
	if(i==1&&j==1)
	f[i][j]=a[i][j];//特判左上角 
	else
	{
		f[i][j]=INF;
		if(i>1)f[i][j]=min(f[i][j],f[i-1][j]+a[i][j]);//  只有不在第一行的时候，才可以从上面过来 
		if(j>1)f[i][j]=min(f[i][j],f[i][j-1]+a[i][j]);//  只有不在第一列的时候，才可以从左面过来 
	}
	cout<<f[n][n];
	return 0;
 } 

三、方格取数

【题目描述】

设有N×N的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

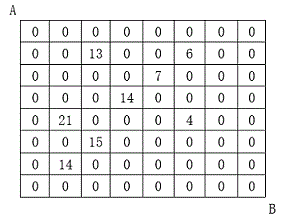
某人从图中的左上角A出发，可以向下行走，也可以向右行走，直到到达右下角的B点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从A点到B点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

【输入】

第一行为一个整数N（N≤10），表示N×N的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。一行“0 0 0”表示结束。

【输出】

第一个整数，表示两条路径上取得的最大的和。

【输入样例】

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

【输出样例】

67

 

 

 

 

#include<bits/stdc++.h>
using namespace std;
const int N=11,INF=0x3f3f3f3f;
int f[2*N][N][N],w[N][N];
int main()
{
    int n;
    cin>>n;

    int a,b,c;
    while(cin>>a>>b>>c,a||b||c) w[a][b]=c;

  for(int k=2;k<=n+n;k++)
     for(int i1=1;i1<=n;i1++)
        for(int i2=1;i2<=n;i2++)
         {
             int j1=k-i1,j2=k-i2;//弄出j1和j2

             if(j1>=1&&j1<=n&&j2>=1&&j2<=n)//假如j合法
            {
             int t=w[i1][j1];

             if(i1!=i2) t+=w[i2][j2];//并且不是同个点

             int &x=f[k][i1][i2];

             x=max(x,f[k-1][i1-1][i2-1]+t);//i1和i2向下
             x=max(x,f[k-1][i1-1][i2]+t);//i1向下和i2向右
             x=max(x,f[k-1][i1][i2-1]+t);//i1向右和i2向下
             x=max(x,f[k-1][i1][i2]+t);//i1向右和i2向右
             }
         }

    cout<<f[n+n][n][n];
    return 0;
}