基于改进的离散PSO算法的FJSP的研究（Python代码实现）

原创于 2024-11-26 15:59:16 发布 · 794 阅读

CC 4.0 BY-SA版权

文章标签：

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、引言

二、算法原理

三、算法步骤

四、实验结果与分析

五、结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Python代码实现

💥1 概述

文献来源：

摘要：柔性作业车间调度问题(Flexible Job-shop Scheduling Problem,FJSP)是经典作业车间调度问题的一个扩展,前者更接近于实际生产。以最小化最大完工时间为目标,提出了一种改进的离散粒子群优化算法。传统粒子群优化算法一般适用于优化连续模型问题,FJSP作为复杂度比较高的组合优化问题,是一种典型的离散模型。提出的算法采用机器负荷平衡机制初始化粒子种群,在粒子的更新过程中引入了3个操作算子来更新粒子的工序排序部分和机器分配部分,这3个算子分别为基于工序排序或机器分配的变异、与个体最优位置之间进行工序先后顺序保留的交叉(POX)操作、与全局最优位置进行随机点保存的交叉(RPX)操作。先后执行以上3个算子以完成粒子的一次更新。这种操作能够使种群较快地收敛于最优解。对标准测试案例进行实验的结果表明,所提算法对解决FJSP具有有效性,并且能够快速地搜索到近似最优解;与其他同类算法相比,所提算法在求解效果和收敛速度上均具有优越性。

关键词：

作业车间调度;离散优化问题;柔性;粒子群优化;

一、引言

FJSP是经典作业车间调度问题的一个扩展，它更接近于实际生产。该问题旨在解决在作业车间中，每个作业包含多个工序，且每个工序可以由多台不同机器加工的情况下，如何安排作业和机器的分配，以最小化最大完工时间。由于FJSP具有高度的复杂性，传统的优化方法难以在合理的时间内找到最优解。因此，本研究提出了一种改进的离散粒子群优化（Particle Swarm Optimization，PSO）算法来解决FJSP。

二、算法原理

传统PSO算法一般适用于优化连续模型问题，而FJSP是一种典型的离散模型。为了将PSO算法应用于FJSP，本研究进行了以下改进：

粒子编码：采用合适的编码方式来表示FJSP的解，即每个粒子表示一个可能的作业和机器分配方案。
初始化种群：采用机器负荷平衡机制来初始化粒子种群，以确保种群的多样性和质量。
操作算子：在粒子的更新过程中，引入基于工序排序或机器分配的变异、与个体最优位置之间进行工序先后顺序保留的交叉（POX）操作、与全局最优位置进行随机点保存的交叉（RPX）操作等三个操作算子来更新粒子的工序排序部分和机器分配部分。

三、算法步骤

生成初始种群：根据种群大小、作业数量、机器数量等参数生成初始种群。
计算适应度：对每个粒子进行解码，计算其对应的FJSP解的适应度（即最大完工时间）。
更新个体最优和全局最优：根据适应度更新每个粒子的个体最优位置和全局最优位置。
迭代更新：在迭代过程中，按照预设的迭代次数或收敛条件，不断使用操作算子更新粒子，并重新计算适应度。
输出最优解：当达到迭代次数或收敛条件时，输出全局最优解。

四、实验结果与分析

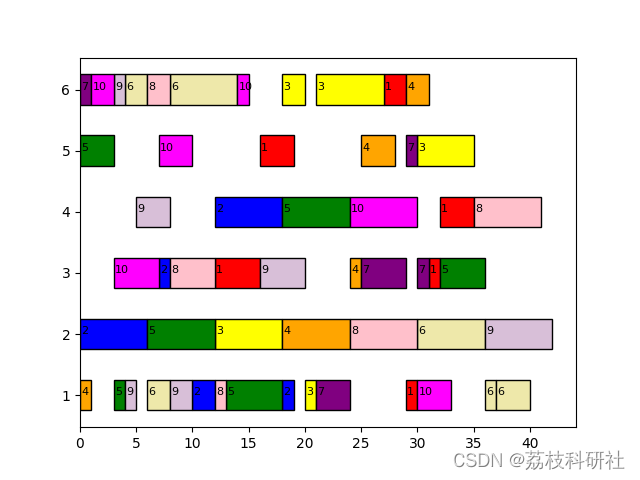
为了验证所提算法的有效性，本研究对标准测试案例进行了实验。实验结果表明，所提算法能够快速地搜索到近似最优解，并且在求解效果和收敛速度上均优于其他同类算法。

五、结论与展望

本研究提出了一种基于改进的离散PSO算法的FJSP求解方法，该方法在求解效果和收敛速度上均表现出优越性。未来，可以进一步探索其他优化算法在FJSP中的应用，以及将FJSP与其他实际问题相结合进行深入研究。

📚2 运行结果

#总共15个Brandimarte文件
for i in range(15):
    #每个数据用例都测试10次，取最好的一次结果，如果为了效率可以每个数据都测试1次
    results = [solve_FJSP(i,j) for j in range(10)]
    Pg_list = [result[0] for result in results ]
    fitness_list = [result[1] for result in results ]
    job_op_num = results[0][2]
    p_table  = results[0][3]
    best_fitness_index = np.argmax(np.array(fitness_list))
    best_fitness = fitness_list[best_fitness_index]
    best_Pg = Pg_list[best_fitness_index]
    #画图，写入.txt文档
    path= './BestFitness/BrandimarteMk'+str(i+1)+'/'
    Decode.decode(best_Pg,job_op_num,p_table,'save',path)
    print(best_Pg,best_fitness)
    with open(path+'best_schedule.txt', 'w') as f:
        f.write(str(best_Pg)+'\n'+str(best_fitness))

部分代码：

# 生成初始种群
# 种群大小，可以根据m和n的值来调整大小，如C*m*n c为一个常系数
# Popsize = 5*p_table.shape[1]*len(job_op_num)
Popsize = 200
encode = Encode(Popsize, p_table, job_op_num)
# 全局选择的染色体
global_chrs = encode.global_selection()
# #局部选择的染色体
local_chrs = encode.local_selection()
# #随机选择的染色体
random_chrs = encode.random_selection()
# 合并三者,得到初始的种群
chrs = np.vstack((global_chrs, local_chrs, random_chrs))

# 以下是关于操作染色体的代码
# 初始的超参数赋值
o_mega = 0.15
c1 = 0.5
c2 = 0.7
pf_max = 0.8
pf_min = 0.2

# 迭代次数，也可以根据m和n的值来调整大小，
# Iter = 5*p_table.shape[1]*len(job_op_num)
Iter = 200

# 得到初始的个体最优位置
P = copy.deepcopy(chrs)
# 得到初始的全局最优位置
# Decode.decode(chr,job_op_num,p_table,'decode')，其中的‘decode’表示不画图，只是计算适应度
fitness_list = [Decode.decode(chr, job_op_num, p_table, 'decode',None) for chr in P]
Pg = P[np.argmin(fitness_list)]
for iter in range(Iter):
    # 计算pf
    pf = pf_max - (pf_max - pf_min) / Iter * iter
    # 更新种群中所有的染色体
    copy_chrs = copy.deepcopy(chrs)
    chrs = [pso.f_operator(job_op_num, p_table, chr, P[index], Pg, pf, o_mega, c1, c2) for index, chr in
            enumerate(copy_chrs)]
    # 更新个体最优位置
    P = np.array([chr1 if Decode.decode(chr1, job_op_num, p_table, 'decode',None) <= Decode.decode(chr2, job_op_num,
                                                                                              p_table, 'decode',None)
                  else chr2 for chr1, chr2 in zip(P, chrs)])
    # 更新全局最优位置
    fitness_list = [Decode.decode(chr, job_op_num, p_table, 'decode',None) for chr in P]
    Pg = P[np.argmin(fitness_list)]

    # for chr in chrs:
    #     print(Decode.decode(chr, job_op_num, p_table, 'decode',None))
    # print("第" + str(iter + 1) + '次循环的最优fitness:', Decode.decode(Pg, job_op_num, p_table, 'decode',None))
    print("第"+str(file_num+1)+'个数据集，第'+str(run_times+1)+'次运行'+'迭代：'+str(iter+1)+'/'+str(Iter))

fitness = Decode.decode(Pg, job_op_num, p_table, 'decode',None)

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]丁舒阳,黎冰,侍洪波.基于改进的离散PSO算法的FJSP的研究[J].计算机科学,2018,45(04):233-239+256.