solidworks如何画阿基米德螺线？

        阿基米德螺线（亦称等速螺线），得名于公元前三世纪希腊数学家阿基米德。阿基米德螺线是一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹。阿基米德在其著作《螺旋线》中对此作了描述。

最初应用：螺旋扬水器

为解决用尼罗河水灌溉土地的难题，阿基米德发明了圆筒状的螺旋扬水器，后人称它为“阿基米德螺旋”。

工程应用：阿基米德螺旋泵

阿基米德螺旋泵的工作原理是当电动机带动泵轴转动时,螺杆一方面绕本身的轴线旋转,另一方面它又沿衬套内表面滚动,于是形成泵的密封腔室。螺杆每转一周,密封腔内的液体向前推进一个螺距,随着螺杆的连续转动,液体螺旋形方式从一个密封腔压向另一个密封腔,最后挤出泵体。螺杆泵是一种新型的输送液体的机械,具有结构简单、工作安全可靠、使用维修方便、出液连续均匀、压力稳定等优点。

生活应用：蚊香的几何特征

将一单盘蚊香光滑面朝上，放置一水平面上，自上俯视，会观察到的蚊香平面图。将这条曲线单独绘制出来，并加上一定的标志，得到了蚊香香条曲线图。点O为直线AB与曲线AB若干交点中位于最中间的一个交点。曲线OA实际上是单盘蚊香的香条外侧边线。观察不同厂牌蚊香的实物，会发现其对应的OA曲线上，接近点的一段，也就是所谓“太极头”部位的曲线，在形状上各有不同，但对于剩下的一大段曲线PA，则具有这样的特征：曲线PA E任取一点Q，假使点Q可在曲线PA上移动，则点Q越接近点A，点Q与点O的直线距离(以r表示)越大；而且，每移动一定角度(以θ表示)，增加的值与该角度成正比。用数学语言描述曲线QA的上述特征，可表示为： △φ=k△θ

在solidworks中，只需要用方程驱动就可以

第一步，点开草图，选择3D草图绘制

第二步，点开草图样条曲线，选择方程式驱动的曲线

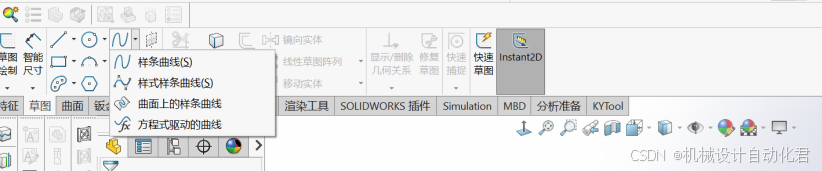
第三步，在设计树中，参数方程式分别输入

Xt=25*cos(2*pi*t)

Yt=25*sin(2*pi*t)

Zt=10*t+5

参数t1=0

        t2=5

第四步，在特征中选择扫描，选中圆形轮廓，以3D草图为线，直径为5mm，薄壁特征设置为单向1mm，曲率显示为斑马条纹