Network Flows Theory, Algorithms, and Applications 3.5节

        本节内容来源于Network Flows Theory, Algorithms, and Applications3.5节，主要介绍流分解算法（flow decomposition algorithms）。

        如图1所示，网络流问题有两种等价的建模形式。第一种是定义在弧（arc）上的流（如2.2节），第二种是定义在路径（path）和环（cycle）上的流。在本节中，我们将针对两种形式的关系展开讨论。

图1 网络流问题的两种形式

1. 弧分解为路径和环        

        定义在弧上的流满足下列关系，即流入的-流出的=-e（i）。此处我们定义e（i）为不平衡（imbalance）。如果e（i）＞0，则称此节点为超额节点（excess node）；如果e（i）＜0，则称此节点为赤字节点（deficit node）；如果e（i）=0，则称此节点为平衡节点（balance node）。

        定义在弧上的流的决策变量是xij；定义在路径和环上的流的决策变量是路径P上的流量f(P)和环上的流量f(W)。弧（i，j）上的流量xij包含所有经过弧（i，j）的路径和环上的流量之和。为表示这一关系，定义如果弧（i，j）包含路径P，则=1； 定义如果弧（i，j）包含环W，则=1。于是有下式：

2. 路径和环分解为弧

        流分解定理：每个路径和环流都可以唯一地表示为非负弧流。相反地，每个非负弧流都可以表示为一个路径和环流（但不一定唯一）。且满足：

        1）每一个有正流的有向路径一定从赤字节点（deficit node）指向超额节点（excess node）；

        2）最多n+m个路径和环具有非零流量；其中最多m个环具有非零流量。

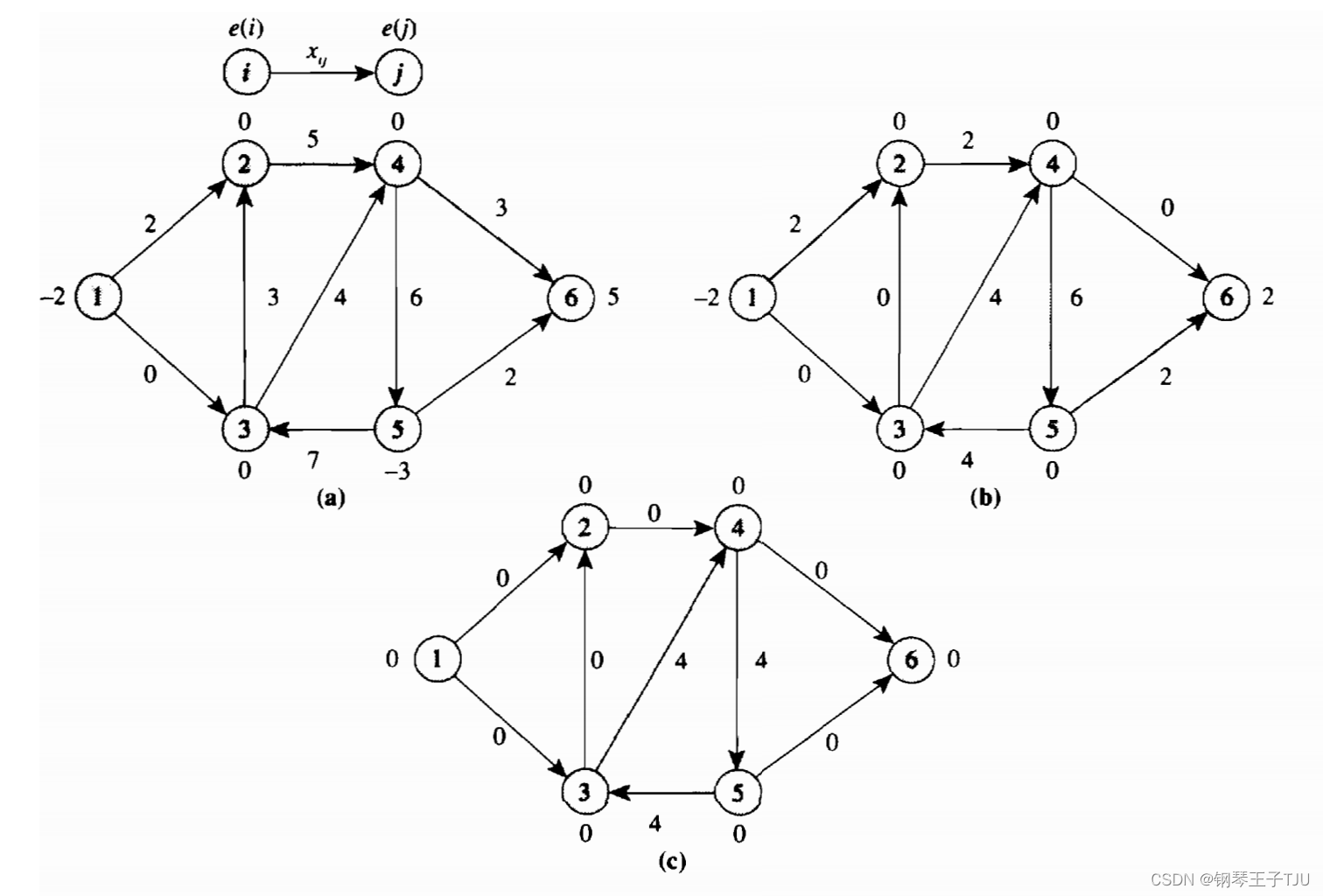
图2  流分解算法

        如图2所示演示了流分解算法。（a）中只有节点1和5是赤字节点（deficit node）。先选择5-3-2-4-6，然后把这个路径流去掉，得到（b）；再选择1-2-4-5-6，把这个路径去掉；最后选择5-3-4-5；此时流都为0，算法终止。流分解算法在O(mn)时间中进行。

3. 增加环定理（argumenting cycle theorem）

        如果在环上给流f（W）增加一个正值后，流仍然是可行的，则称G中的一个环W（不必要是有向的）是对应于流x的增加环。

        x和x°是网络流问题的任意两个可行解。那么x等于x°加上网络G（x°）上最多m个定向循环的流量。x的成本等于x°的成本加上这些增加环上的流成本。

4. 负循环最优性定理（negetive cycle optimality theorem）

        最小成本流问题中，一个可行解x*是最优解当且仅当残差网络G（x*）不包含负成本有向环。