网络流基础、最大流最小割定理以及证明

最新推荐文章于 2025-02-15 15:58:33 发布

syddf_shadow

最新推荐文章于 2025-02-15 15:58:33 发布

阅读量1.2w

点赞数 24

分类专栏：图论

本文链接：https://blog.csdn.net/yjr3426619/article/details/82715779

版权

本文介绍了网络流的基础概念，包括容量网络、可行流和最大流。最大流最小割定理指出，网络流的最大流量等于最小割的容量。通过增广路的概念解释了如何寻找最大流，并证明了最大流与最小割之间的等价关系。最后，讨论了寻找增广路在求解最大流算法中的关键作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

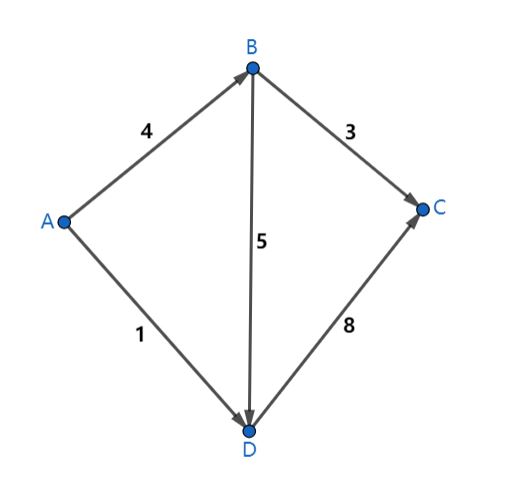
这里写图片描述

网络流的基本概念

网络流问题都是建立在类似上图的有向图之上，有向图的边的权值代表容量。其中A代表源点，C代表汇点，一般考察的问题情景就是从A中流出流量，经过这些有向边，最终汇集到C中。像这样的具有源点和汇点，并且每条边的权值均为正数的有向图就被称作是容量网络，图中的这些边被称作是弧，弧的权值被称作弧的容量，它代表着能够通过这条弧的最大流量。而经过弧上的实际流量被称作弧的流量，所有这些弧的流量所组成的集合就是所谓的网络流。

直观上不难发现符合实际情况的网络流的特点，或者说是限制条件。首先每条弧上的流量不能超过其容量，还有对于除了源点和汇点以外的每个点来说，流入它的流量之和必须与从它流出的流量之和相等，即平衡条件。那么满足这两个条件的网络流就被称作是可行流，可行流的流量定义为从源点所流出的所有流量之和。在所有的可行流中，流量最大的那个被称作是最大流。

对于一串顶点序列 $(U, U 1, U 2, U 3, \dots, V)$ ，如果满足 $U$ 是源点， $V$ 是汇点，并且序列中每相邻两个顶点之间均存在一条弧，那么就称这个顶点序列为一条链，注意这里并不要求这条弧的方向一定与有向图中的方向一致，在链中，弧被分为前向弧和后向弧，前向弧指在链中顶点的顺序与容量网络中弧的方向一致的弧，而后向弧则是方向不一致的弧。例如对于上图而言， $(A, D, B, C)$ 也是一条链，但是其中 $< A, D > 、 < B, C >$ 是前向弧， $< D, B >$ 是后向弧。

有了链的定义就可以引出增广路的概念，对于可行流的一条链 $P$ ，如果满足：
1. $P$ 中所有的前向弧的流量小于容量
2. $P$ 中所有的后向弧的流量均大于零
那么这条链 $P$ 就被称作增广路。为什么要叫作增广路呢？因为增广路上的所有前向弧都是可以继续添加流量的（增加的流量不能超过每条前向弧的容量与流量之差），而反向弧上的流量都是可以继续减少的（减少的流量不能超过反向弧的流量），这两种措施都会使得这个可行流的流量变得更大。