k 近邻（k-Nearest Neighbor， kNN）算法

無量空所

已于 2025-01-19 10:26:05 修改

阅读量565

点赞数 26

分类专栏：机器学习文章标签：算法机器学习人工智能

于 2025-01-19 10:25:47 首次发布

本文链接：https://blog.csdn.net/m0_67804957/article/details/145237550

版权

机器学习专栏收录该内容

7 篇文章

订阅专栏

3.2 曼哈顿距离（Manhattan Distance）

3.3 巴氏距离（bhattacharyya 距离）

一、基本思想

模板匹配：要确定一个样本的类别，可以计算它与所有训练样本的距离，然后找出和该样本最接近的 k 个样本，统计这些样本的类别进行投票，票数最多的那个类就是分类结果。

二、基本概念

1、举例

有 A、 B 两类样本，红色方块是待分类样本，我们寻找离该样本最近的 k 个训练样本，然后统计这 k 个训练样本所属的类别，当 k=9 时， A 类样本有 5 个， B 类样本有 4 个，因此，把这个待分类样本判定为 A 类。

2、算法流程

给定 $l$ 个训练样本 $(x_i,y_i)$ ，其中 $x_i$ 是特征向量， $y_i$ 是标签，设定一个参数 $k$ ，假设样本共有 $c$ 种类别，待分类样本的特征向量为 x

2.1 分类问题

在训练样本集中找出离 x 最近的 $k$ 个样本，假设这些样本的集合为 N。
统计集合 N 中每一类样本的个数 $C_i, i = 1,2,...,c$ 。
最终的分类结果为 $arg max_i C_i$ ，即最大的值对应的那个类别。

2.2 预测问题

在训练样本集中找出离 x 最近的 $k$ 个样本，假设这些样本的集合为 N。
如果是回归预测，计算 $k$ 个训练样本的标签值的均值
$k$ 个邻居贡献相同时，可采用 $\hat{y} = \left( \sum_{i=1}^{k} y_{i} \right ) / k$ ；也可采用带权重的方案 $\hat{y} = \left( \sum_{i=1}^{k} w_iy_{i} \right) / k$

注：k=1 的近邻算法称为最近邻算法

3、距离定义

3.1 欧几里得距离（欧式距离）

n 维欧式空间中两点之间的直线距离，对于 $\mathbb {R}^n$ 空间中的两个点 x 和 y，它们之间的距离定义为

注：使用该方法时应将特征向量的每个分量归一化，以减少因为特征值的尺度范围不同所带来的干扰，否则数值小的特征分量会被数值大的特征分量淹没。

3.2 曼哈顿距离（Manhattan Distance）

两个点在标准坐标系上的绝对轴距总和。

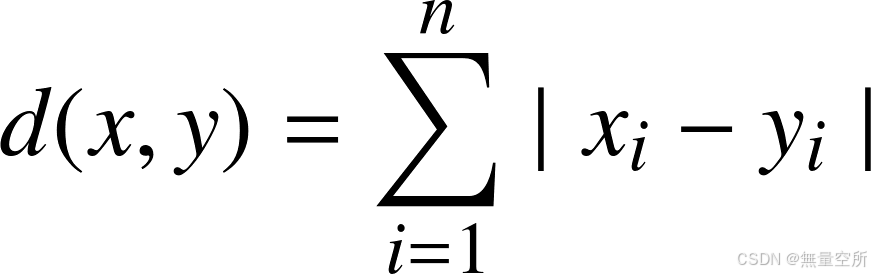
绿色的线表示的是欧式距离；
红色的线表示曼哈顿距离；
黄、蓝两条色与曼哈顿距离相等，称为等价曼哈顿距

3.3 巴氏距离（bhattacharyya 距离）

两个离散型或连续型概率分布的相似性。

离散型

$x_i, y_i$ 是两个随机变量取某一值的概率。两个向量越相似，这个距离值越小。

连续型

$f(x),g(y)$ 是两个随机变量概率密度函数

三、代码实现

1、手动实现

import numpy as np
from collections import Counter
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler


# 定义 kNN 算法
def k_nearest_neighbors(X_train, y_train, X_test, k=3):
    predictions = []
    for test_point in X_test:
        distances = []
        for train_point in X_train:
            distance = np.sqrt(np.sum((test_point - train_point) ** 2))
            distances.append(distance)
        # 根据距离进行排序，并获取最近的 k 个邻居
        nearest_neighbors = np.argsort(distances)[:k]
        # 获取邻居的标签
        neighbor_labels = [y_train[i] for i in nearest_neighbors]
        # 统计邻居中出现次数最多的标签作为预测结果
        most_common_label = Counter(neighbor_labels).most_common(1)[0][0]
        predictions.append(most_common_label)
    return predictions


# 加载 iris 数据集
iris = load_iris()
X = iris.data
y = iris.target

# 将数据集分割为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=41)
# scaler = StandardScaler()
# X_train = scaler.fit_transform(X_train)
# X_test = scaler.transform(X_test)

# 使用 kNN 进行分类预测
predictions = k_nearest_neighbors(X_train, y_train, X_test, k=5)

# 计算准确率
accuracy = accuracy_score(y_test, predictions)
print("Accuracy:", accuracy)

2、sklearn库实现

from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score


# 载入iris数据集
iris = datasets.load_iris()
# 只使用前面样本特征
X = iris.data
# 样本标签值
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=41)

# 创建kNN分类器
knn = KNeighborsClassifier()
knn.fit(X_train, y_train)
predictions = knn.predict(X_test)

accuracy = accuracy_score(y_test, predictions)
print("Accuracy:", accuracy)